Standard Hydrogen Electrode

Have you ever wondered how scientists decide the “zero point” for measuring the electrical potential of all electrodes? The answer is Standard Hydrogen Electrode (SHE). SHE serves as the reference with an assigned potential of exactly 0.00 V. The SHE’s standardized conditions (1 M H⁺, 1 atm $\mathrm{H}_2$, 25°C) ensure accurate and consistent measurements of electrode potentials, which are essential for reliable electrochemical experiments and industrial processes. The SHE is used as a reference electrode in pH meters, providing a stable reference for measuring the voltage difference and determining the pH of solutions.

This Story also Contains

1. Standard Hydrogen Electrode
2. Application Of Standard Hydrogen Electrode
3. Some Solved Examples
4. Summary

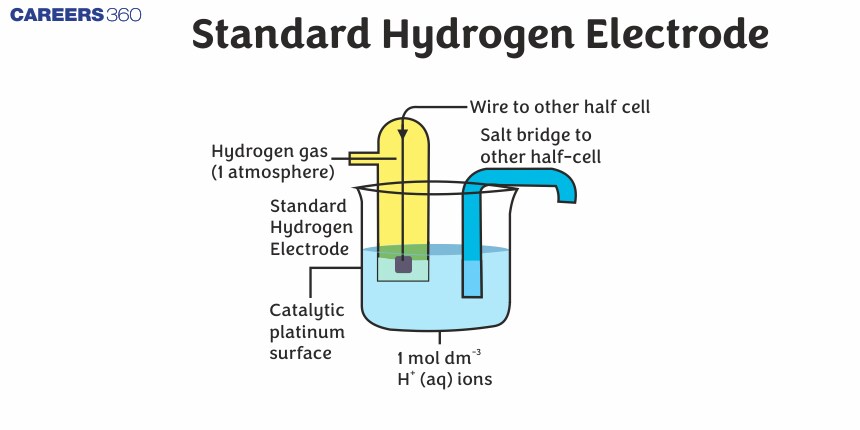
Standard Hydrogen Electrode

A hydrogen electrode in which the pressure of hydrogen gas is maintained at 1 atm and the concentration of H+ ions in the solution is 1M, is called a standard hydrogen electrode (SHE).
SHE half reaction Electrode potential

$\mathrm{H}_2 \rightarrow 2 \mathrm{H}^{+}+2 \mathrm{e}^{-} 0.0 \mathrm{~V}$ (Anode)

$2 \mathrm{H}^{+}+2 \mathrm{e}^{-} \rightarrow \mathrm{H}_2 0.0 \mathrm{~V}$ (Cathode)

• The emf of a standard hydrogen electrode is taken as 0.00 V at all temperatures.
• It is a reversible electrode.
• It is used as a primary reference electrode.
• The potential of other species can be calculated by conducting a cell with SHE as one of the electrodes and then calculating the potential difference by various methods.

• A hydrogen electrode in which the pressure of hydrogen gas is maintained at 1 atm and the concentration of H⁺ ions in the solution is 1M, is called a standard hydrogen electrode (SHE).
  SHE half reaction Electrode potential

$\mathrm{H}_2 \rightarrow 2 \mathrm{H}^{+}+2 \mathrm{e}^{-} 0.0 \mathrm{~V}$ (Anode)

$2 \mathrm{H}^{+}+2 \mathrm{e}^{-} \rightarrow \mathrm{H}_2 0.0 \mathrm{~V}$ (Cathode)

• A standard hydrogen electrode emf is taken as 0.00 V at all temperatures.
• It is a reversible electrode.
• It is used as a primary reference electrode.
• The potential of other species can be calculated by conducting a cell with SHE as one of the electrodes and then calculating the potential difference by various methods.

• This equation gives the relationship between electrode potential and the concentration of ions in the solution. In other words, it shows the dependency of electrode potential on the concentration of the ions with which the electrode is reversible.

  For a single electrode involving the reduction process,

  $\mathrm{Mn}^{+}+\mathrm{ne}^{-} \rightarrow \mathrm{M}(\mathrm{s})$

  The reaction quotient Q is defined as aM[M

  ⇒$\mathrm{E}=\mathrm{E}^{\circ}-\frac{\mathrm{RT}}{\mathrm{nF}} \ln Q$

  This is the Nernst equation which helps us to calculate the non-standard EMF of any Half cell. It can be extended to full of any half cell. It can be extended to full cell which we will be learning later.

  Now, at 25∘C or 298 K

  $\begin{aligned} & E=E^{\circ}-\frac{2.303 \times 8.314 \times 298}{n \times 96500} \log _{10} \frac{[M]}{\left[M^{n+}\right]} \\ & E=E^{\circ}-\frac{0.059}{n} \log _{10} \frac{[M]}{\left[M^{n+}\right]}\end{aligned}$

Here $\mathbf{R}=$ Gas constant
$\mathrm{T}=$ Absolute temperature
$\mathrm{E}^{\circ}=$ Standard Emf of the cell
E = Electrode potential of cell
F = Faraday number
$\mathbf{n}=$ number of electrons transferred

• If the electrode is solid its activity mass is taken as one.
• For an electrochemical cell having a net reaction:

  $
  \mathrm{xA}+\mathrm{yB} \xrightarrow{\mathrm{ne}^{-}} \mathrm{mC}+\mathrm{nD}
  $
  The emf can be calculated as

  $
  \text { Ecell }=\mathrm{E}^{\mathrm{o}} \text { cell }-\frac{0.059}{\mathrm{n}} \log \frac{[\mathrm{C}]^{\mathrm{m}}[\mathrm{D}]^{\mathrm{n}}}{[\mathrm{~A}]^x[\mathrm{~B}]^{\mathrm{y}}}
  $

In using the above equation, the following facts should be kept in mind.

• The activity of aq. ions are expressed in terms of their concentration.
• Activity of gases is expressed in terms of their partial pressures.
• The activity of solids is taken to be unity.
• n, the number of electrons transferred should be calculated from the balanced net cell reaction.

Application Of Standard Hydrogen Electrode

The Standard Hydrogen Electrode (SHE) is a reference electrode used in electrochemical measurements. Its applications and significance are.

1. Reference Electrode for Measuring Electrode Potential

• Standardization: The SHE is used as a reference point to measure the electrode potentials of other half-cells. By definition, the SHE has a potential of 0.00 V under standard conditions (1 M H⁺, 1 atm H₂, 25°C).
• Comparison: Electrochemical cells are set up with the SHE as one half-cell and another electrode as the other half-cell. The potential difference between them is measured to determine the potential of the second electrode.

2. Electrochemical Series

• Determining Standard Electrode Potentials: The SHE is central in defining the electrochemical series, which ranks electrodes based on their standard electrode potentials relative to the SHE.
• Predicting Reactions: The electrochemical series helps predict the direction of redox reactions, their feasibility, and the voltage generated in electrochemical cells.

3. pH Measurement

• pH Reference: In pH meters, the SHE can serve as a reference electrode. Its potential is used to measure the voltage difference with a pH-sensitive electrode, determining the pH of a solution.

4. Corrosion Studies

• Corrosion Potential Measurement: The SHE is used to measure the corrosion potential of metals and alloys in various environments, which helps in understanding and mitigating corrosion.

5. Electrolysis and Industrial Processes

• Electrolytic Cells: In electrolysis, the SHE helps design and control processes by providing a stable reference for measuring cell potentials and optimizing conditions.

Recommended topic video on(standard hydrogen electrode)

Some Solved Examples

Example.1

1. Consider the following cell with hydrogen electrodes at different pressures p₁ and p₂.
$\mathrm{Pt}, \mathrm{H}_2\left(p_1\right)\left|\begin{array}{c}\mathrm{H}^{+}(\mathrm{aq}) \\ 1 \mathrm{M}\end{array}\right| \mathrm{H}_2\left(p_2\right), \mathrm{Pt}$
The EMF of the cell is given by:

1) $\frac{\mathrm{RT}}{\mathrm{F}} \ln \frac{\mathrm{p}_1}{\mathrm{p}_2}$

2) (correct) $\frac{\mathrm{RT}}{2 \mathrm{~F}} \ln \frac{\mathrm{p}_1}{\mathrm{p}_2}$

3) $\frac{\mathrm{RT}}{\mathrm{F}} \ln \frac{\mathrm{p}_2}{\mathrm{p}_1}$

4)$\frac{\mathrm{RT}}{2 \mathrm{~F}} \ln \frac{\mathrm{p}_2}{\mathrm{p}_1}$

Solution

For the given concentration cell, the Nernst equation can be written as

$\begin{aligned} \mathrm{E}_{\text {cell }} & =0.059\left[\mathrm{pH}_{\mathrm{a}}-\mathrm{pH}_{\mathrm{c}}+\frac{1}{2} \log \frac{\left(\mathrm{pH}_2\right)_{\mathrm{a}}}{\left(\mathrm{pH}_2\right)_{\mathrm{c}}}\right] \\ & =0.059\left[0-0+\frac{1}{2} \log \frac{p_1}{p_2}\right] \\ & =\frac{0.059}{2} \log \frac{p_1}{p_2}=\frac{R T}{2 F} \ln \frac{p_1}{p_2}\end{aligned}$

Hence, the answer is the option (2).

Example.2

2. A hydrogen electrode placed in a solution containing sodium acetate and acetic acid in the ratio of x: y and y : x has an electrode potential value E₁ and E₂ volts respectively at 25^oC. The pK_a value of acetic acid is:

1) (correct) $\frac{-\left(E_1+E_2\right)}{2 \times 0.059}$

2) $\frac{\left(E_1+E_2\right)}{2 \times 0.059}$

3) $\frac{E_2-E_1}{2 \times 0.059}$

4) $\frac{-\left(E_1+E_2\right)}{0.059}$

Solution

The reaction occurring in the hydrogen electrode is given below:

$\mathrm{H}^{+}+\mathrm{e}^{-} \longrightarrow \frac{1}{2} \mathrm{H}_2$

Using the Nernst Equation, the electrode potential can be written as

$\mathrm{E}=-0.059 \log \frac{1}{\left[\mathrm{H}^{+}\right]}=-0.059 \mathrm{pH}$

In the two given cases, the Hydrogen ions are obtained by buffer solution having the ratio of Salt : Acid as $\mathrm{x}: \mathrm{y}$ and $\mathrm{y}: \mathrm{x}$

The pH of an acidic buffer can be calculated as
$\begin{aligned} & \mathrm{pH}=\mathrm{pK}_{\mathrm{a}}+\log \left(\frac{\text { Salt }}{\text { Acid }}\right) \\ & \therefore \mathrm{pH}_1=\mathrm{pK}_{\mathrm{a}}+\log \frac{\mathrm{x}}{\mathrm{y}}\end{aligned}$
Similarly,

$\mathrm{pH}_2=\mathrm{pK}_{\mathrm{a}}+\log \frac{\mathrm{y}}{\mathrm{x}}$

Thus, the respective electrode potentials can be written as

$\begin{aligned} \therefore \mathrm{E}_1 & =-0.059 \mathrm{pH}_1 \\ \mathrm{E}_2 & =-0.059 \mathrm{pH}_2\end{aligned}$

pH2=pKa+log⁡yr

Now, adding the two potentials gives us

$\begin{aligned} & \left(\mathrm{E}_1+\mathrm{E}_2\right)=-0.059\left(\mathrm{pK}_{\mathrm{a}}+\log \frac{\mathrm{x}}{\mathrm{y}}\right)-0.059\left(\mathrm{pK}_{\mathrm{a}}+\log \frac{\mathrm{y}}{\mathrm{x}}\right) \\ & \left(\mathrm{E}_1+\mathrm{E}_2\right)=-0.059 \times 2 \times \mathrm{pKa} \\ & \mathrm{pK}_{\mathrm{a}}=\frac{-\left(\mathrm{E}_1+\mathrm{E}_2\right)}{2 \times 0.059}\end{aligned}$
Hence, the answer is the option (1).

Example.3

3. Select the correct statement out of the following.

1) The absolute value of potential is defined.

2) (correct) The Potential of SHE is arbitrarily assigned zero value.

3)In SHE, the pH of the solution is 7

4)In SHE, the pressure of H₂ (g) is 760atm.

Solution

The absolute value of the potential is not defined. We can only measure the potential difference. As a convention, the SHE is assigned a value of zero, and the potential of other species is measured concerning the SHE.

Hence, the answer is option (2).

Example 4

The standard reduction potential of Hydrogen is zero because

1) (correct)It is taken as a standard reference.

2)It is the easiest to oxidize.

3)It has a single electron.

4)It is electronegative

Solution

The absolute electric potential for an electrode cannot be measured without forming a cell. Therefore, hydrogen is taken as a standard reference and its potential is taken as zero.

Hence, the answer is option (1).

Practice More Questions With The Link Given Below

Summary

The Standard Hydrogen Electrode was developed to provide a consistent and reliable reference point for measuring electrode potentials, which is essential for standardizing electrochemical measurements, understanding reaction dynamics, and advancing scientific and industrial applications in electrochemistry.

Also read :