What is Coordinate Axes -Examples & Solutions

To represent the position of a point in a plane, we use a specific set of lines known as coordinate axes. For instance, in a 2D plane, two coordinate axes are essential to define a point's position. The plane created by the intersection of these axes is referred to as the Cartesian plane. In two-dimensional space, coordinate axes help us to identify the point's position by measuring its projections along each axis. These projections represent the length and width, enabling us to determine the exact position of the point in terms of its horizontal and vertical coordinates.

This Story also Contains

1. Coordinate Axes
2. Conversion Sign of coordinate
3. Polar Coordinate of a Point
4. Solved Examples Based on Coordinate Axes

In this article, we will cover the concept of Coordinate axes. This category falls under the broader category of Coordinate Geometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. A total of seventeen questions have been asked on JEE MAINS (2013 to 2023) from this topic including one in 2015, and one in 2019.

Coordinate Axes

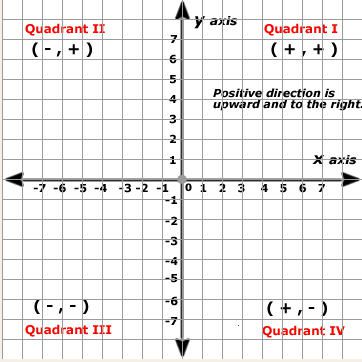
The Cartesian coordinate system, also called a rectangular coordinate system, is based on a two-dimensional plane consisting of the x-axis and the y-axis. Perpendicular to each other, the axes divide the plane into four sections. Each section is called a quadrant; the quadrants are numbered counterclockwise as shown in the figure below

A two-dimensional plane where the

• the x-axis is the horizontal axis

• the y-axis is the vertical axis

Let XOX and YOY be two fixed straight lines at a right angle. XOX is called the x-axis or horizontal axis, YOY is called the y-axis or vertical axis and the point of intersection of both the axes i.e., O is called the origin. Two axes divide the plane into four regions, called quadrants.

Since X’OX is perpendicular to Y’OY, this system of representation is called a rectangular (or orthogonal) coordinate system.

When the axes X'OX and Y’OY are not at right angles, they are said to be oblique axes.

A point in the plane is defined as an ordered pair, (x,y), such that x is determined by its horizontal distance from the origin and y is determined by its vertical distance from the origin.

The distance from a point to the vertical or y-axis is called the abscissa or x-coordinate of the point.

The distance from a point to the horizontal or x-axis is called the ordinate or y-coordinate of the point.

We can represent the point  (3,−1) in the plane by moving three units to the right of the origin in the horizontal direction, and one unit down in the vertical direction.

Conversion Sign of coordinate

Polar Coordinate of a Point

Consider the figure,

If OP = r and ∠XOP = θ. Then, the ordered pair of real numbers (r, θ) is called the polar coordinates of the point P.

From the figure

$\mathrm{OM}=\mathrm{x}=\mathrm{r} \cos \theta$

$P M=y=r \sin \theta$

$\begin{aligned} & \text { Square and add, } \\ & \mathrm{OM}^2+\mathrm{PM}^2=\mathrm{x}^2+\mathrm{y}^2=\mathrm{r}^2 \\ & \Rightarrow \mathrm{r}=\sqrt{\mathrm{x}^2+\mathrm{y}^2}\end{aligned}$

Recommended Video Based on Coordinate Axes

Solved Examples Based on Coordinate Axes

Example 1: A point on the straight line, $3 x+5 y=15$ which is equidistant from the coordinate axes will lie only in : [JEE MAINS 2019]

Solution: Coordinate system that specifics each point uniquely in a plane by a pair of numerical coordinates.

Let the point be

$
(h, k)
$
since point is equidistance from the axes
$
\begin{aligned}
& h=k \\
& 3 h+5 h=15 \\
& 8 h=15 \\
& h=\frac{15}{8}
\end{aligned}
$

1st quadrant $x>0, y>0$ and intersection of line $y=x$ and $y=-x$

will also give a point

for $y=x, \quad 3 x+5 x=15$

for $y=-x, \quad x=\frac{15}{8}$

$3 x-5 x=15=x=-\frac{15}{2} 2^{\text {nd }}$ quadrant
$
x<0, y>0
$

So 1st and 2nd quadrant:

as $y=x, y=-x$ all points on these lines are equidistant from coordinate axes so we find their intersection and determine the quadrant.

$\begin{aligned} & x>0, y>0=1^{s t} \\ & x<0, y>0=2^{n d}\end{aligned}$

Hence, the answer is $1^{\text {st }}$ and $2^{\text {nd }}$.

Example 2: The number of points, having both co-ordinates as integers, that lie in the interior of the triangle with vertices (0, 0), (0, 41), and (41, 0), is : [JEE MAINS 2015]

Solution:

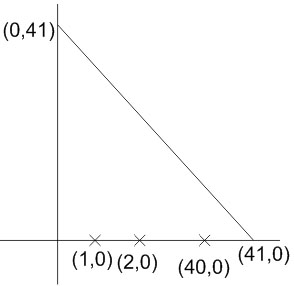
Number of integral points on the line $x=1$, is 39

Number of integral points and the line $x=2$ is $: 38$

Similarly, we get

Total integral points = $39+38+\ldots . .2+1$

$\begin{aligned} & =\frac{39.40}{2} \\ & =780\end{aligned}$

Hence, the answer is 780.

Example 3: Point (-5, 2) lies in which quadrant.

Solution: From the table, X-coordinate is -ve and Y-coordinate is +ve. So, the point lies on the 2nd quadrant.

Example 4: A point lies on the X-axis at a distance of 10 units from the Y-axis, then the coordinates of the point will be

Solution: Given that the point lies on the X-axis at a distance of 10 units from the Y-axis, the point may be on the left of the Y-axis or right of the Y-axis. So, X-coordinate will be -10 or +10. And, the point lies on the X-axis, so the Y-coordinate will be 0.

So, the coordinate of the point will be (-10, 0) or (+10, 0).

Example 5: What is the distance of the point (-3, -5 ) from the y-axis?

Solution :

Given that the point lies on the X-axis at a distance of 10 units from the Y-axis, so the point may be on the left of the Y-axis or right of the Y-axis. So, X-coordinate will be -10 or +10.

And, the point lies on the X-axis, so the Y-coordinate will be 0.

So, the coordinate of the point will be (-10, 0) or (+10, 0)

Distance is always positive and distance will be 3 units

Hence, the answer is 3.

Example 5: What is the distance of point (- 3, - 4) from the origin?

Solution: The distance of point(-3,-4) from origin:

$\begin{aligned} & r=\sqrt{x^2+y^2} \\ & r=\sqrt{(-3)^2+(-4)^2} \\ & r=5\end{aligned}$

Hence, the answer is 5.