Rotation of Axes

In this article, we will cover the concept of Rotation of axes. This category falls under the broader category of Coordinate Geometry, which is a crucial Chapter in class 11 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. A total of five questions have been asked on JEE MAINS( 2013 to 2023) from this topic in the last few years.

This Story also Contains

1. What is the Rotation of Axes About Origin?
2. Formula for rotation of axes
3. Derivation of formula to calculate the rotation of axes
4. Applications in Coordinate Geometry
5. Solved Examples Based on Rotation Of Axes
6. Summary

What is the Rotation of Axes About Origin?

Cartesian coordinate system where the x-axis and y-axis intersect at the origin (0, 0) is shown below. The x-axis points horizontally to the right, and the y-axis vertically upwards.

Formula for rotation of axes

Now, if we want to rotate this coordinate system by an angle θ clockwise or anticlockwise about the origin, the new coordinates $\left(x^{\prime}, y^{\prime}\right)$ of any point $(x, y)$ in the original system can be found using the following formulas:

$x^{\prime}=x \cos \theta-y \sin \theta$

$y^{\prime}=x \sin \theta+y \cos \theta$

Here, $\theta$ is the angle of rotation. These formulas effectively rotate the original coordinates $(x, y)$ by θ degrees to obtain the new coordinates $\left(x^{\prime}, y^{\prime}\right)$. It's important to note that clockwise rotation is considered negative $\theta$, while anticlockwise rotation is positive.

$P(x, y)$ is the point in the original coordinate system and axes are rotated by an angle $\theta$ anticlockwise direction about the origin. Then, the coordinates of point P with respect to the new coordinate system is $(X, Y)=$ $(x \cos \theta+y \sin \theta, y \cos \theta-x \sin \theta)$.

Derivation of formula to calculate the rotation of axes

Let us find the coordinates of point P with respect to the new coordinate system

OX and OY are an original system of coordinate axes and OX’ and OY’ are the new system of coordinate axes. PM and PN are perpendicular to OX and OX’ and also NL and NQ are perpendicular to OX and PM.

We have

From the figure:

$
\begin{aligned}
\mathrm{OM} & =\mathrm{x}, \mathrm{PM}=\mathrm{y}, \mathrm{ON}=\mathrm{X} \text { and } \mathrm{PN}=\mathrm{Y} \\
\text { Now, } \quad \mathrm{x} & =\mathrm{OM}=\mathrm{OL}-\mathrm{ML}
\end{aligned}
$
$\because$ angle between two lines $=$ angles between their perpendiculars
$
\begin{aligned}
& =\mathrm{OL}-\mathrm{QN}=\mathrm{ON} \cos \theta-\mathrm{PN} \sin \theta \\
& =\mathrm{X} \cos \theta-\mathrm{Y} \sin \theta
\end{aligned}
$
i.e. $\mathbf{x}=\mathbf{X} \cos \theta-\mathbf{Y} \sin \theta$

And,
$
\begin{aligned}
\mathrm{y} & =\mathrm{PM}=\mathrm{PQ}+\mathrm{QM}=\mathrm{PQ}+\mathrm{NL} \\
& =\mathrm{PN} \cos \theta+\mathrm{ON} \sin \theta \\
& =\mathrm{Y} \cos \theta+\mathrm{X} \sin \theta
\end{aligned}
$
i.e. $\mathbf{y}=\mathbf{Y} \cos \theta+\mathbf{X} \sin \theta$

By solving (i) and (ii), we get

$x=x \cos \theta+y \sin \theta$

$Y=y \cos \theta-x \sin \theta$

$\begin{array}{|c|c|c|}
\hline & x & y \\
\hline X & \cos \theta & \sin \theta \\
\hline Y & -\sin \theta & \cos \theta \\
\hline
\end{array}$

Applications in Coordinate Geometry

The rotation of axes finds extensive application in coordinate geometry, particularly in simplifying equations of curves. For instance, if we have a conic section whose equation is given in terms of x and y, the equation becomes simpler when rotated to align with the new coordinate axes $\left(x^{\prime}, y^{\prime}\right)$. This technique also helps in solving geometric problems involving angles and distances more intuitively.

Solved Examples Based on Rotation Of Axes

Example 1: Write the equation $x y=1$ in terms of a rotated $x^{\prime} y^{\prime}$ -system if the angle of rotation from the $\mathbf{X}$-axis to the $x^{\prime}$ -axis is $45^{\circ}$.

Solution:

$\begin{aligned} & x=x^{\prime} \cos 45^{\circ}-y^{\prime} \sin 45^{\circ} \\ & y=x^{\prime} \sin 45^{\circ}+y^{\prime} \cos 45^{\circ} \\ & x y=1 \\ & {\left[\frac{1}{\sqrt{2}}\left(x^{\prime}-y^{\prime}\right)\right]\left[\frac{1}{\sqrt{2}}\left(x^{\prime}+y^{\prime}\right)\right]=1} \\ & \frac{1}{2}\left(x^{\prime 2}-y^{\prime 2}\right)=1 \\ & \frac{x^{\prime 2}}{2}-\frac{y^{\prime 2}}{2}=1 \\ & \text { Hence, the answer is } \frac{x^{\prime 2}}{2}-\frac{y^{\prime 2}}{2}=1\end{aligned}$

Example 2: If a vertex of a triangle is $(1,1)$ and the midpoints of two sides through this vertex are $(-1,2)$ and $(3,2)$, and if this triangle is rotated with $45^{\circ}$ about the origin O then the centroid of the triangle is

Solution: The centroid formula is given by

$\left(\frac{x_1+x_2+x_3}{3}, \frac{y_1+y_2+y_3}{3}\right)$

$\mathrm{A}\left(\mathrm{x}_1, \mathrm{y}_1\right) ; \mathrm{B}\left(\mathrm{x}_2, \mathrm{y}_2\right)$ and $\mathrm{C}\left(\mathrm{x}_3, \mathrm{y}_3\right)$ are the vertices of $\Delta$ ABC.

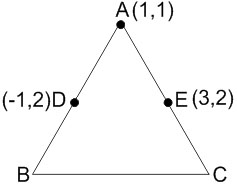
The Coordinate of B is $(-3,3)$ and the coordinate of C is $(5,3)$.

Centroid is $\left(\frac{1-3+5}{3}, \frac{1+3+3}{3}\right)=\left(1, \frac{7}{3}\right)$

Now it's rotated $45^{\circ}$, which means axis rotated $-45^0$ about origin O then new centroid so use $\theta=-45^{\circ}$

$\begin{gathered}X=x \cos \theta+y \sin \theta=1 \cdot \frac{1}{\sqrt{2}}+\frac{7}{3} \cdot \frac{-1}{\sqrt{2}}=\frac{-4}{3 \sqrt{2}} \\ Y=y \cos \theta-x \sin \theta=\frac{7}{3} \cdot \frac{1}{\sqrt{2}}-1 \cdot \frac{-1}{\sqrt{2}}=\frac{10}{3 \sqrt{2}}\end{gathered}$

Hence, the answer is $\left(1, \frac{7}{3}\right)$.

Example 3: At what point the axes be shifted without rotation so that the equation $a x^2+2 h x y+b y^2+2 g x+2 f y+c=0$ does not contain terms in x, y and constant term ?

Solution: Let the origin be shifted to $\left(\mathrm{x}_1, \mathrm{y}_1\right)$. Then, $\mathrm{x}=\mathrm{X}+\mathrm{x}$ and $y=Y+y_1$

Substituting $x=X+x_1$ and $y=Y+y_1$ in ax ${ }^2+2 h x y+b^2+2 g x+2 f y+c=0$, we get
$
\begin{aligned}
& a\left(\mathrm{X}+x_1\right)^2+2 \mathrm{~h}\left(\mathrm{X}+x_1\right)\left(\mathrm{Y}+y_1\right)+b\left(\mathrm{Y}+y_1\right)^2+2 g\left(\mathrm{X}+x_1\right)+2 f\left(\mathrm{Y}+y_1\right)+c=0 \\
& a \mathrm{X}^2+2 h \mathrm{XY}+b \mathrm{Y}^2+2 \mathrm{X}\left(a x_1+h y_1+g\right)+2 \mathrm{Y}\left(h x_1+b y_1+f\right)+a x_1^2+2 h x_1 y_1+b y_1^2+2 g \mathrm{gx}_1+2 f y_1+c=0
\end{aligned}
$

This equation will be free from the terms containing $\mathrm{X}, \mathrm{Y}$ and constant term, if
$
\begin{aligned}
& a x_1+h y_1+g=0 \\
& h x_1+b y_1+f=0
\end{aligned}
$
$
\text { and, } \mathrm{ax}_1^2+2 h \mathrm{x}_1 \mathrm{y}_1+\mathrm{by}_1^2+2 \mathrm{gx}_1+2 \mathrm{fy}_1+\mathrm{c}=0
$

Now, $a x_1^2+2 h x_1 y_1+b y_1^2+2 g x_1+2 \mathrm{fy}_1+c=0$
$
\begin{array}{ccc}
\Rightarrow & \mathrm{x}_1\left(\mathrm{ax}_1+\mathrm{hy}_1+\mathrm{g}\right)+\mathrm{y}_1\left(\mathrm{hx}_1+\mathrm{by}_1+\mathrm{g}\right)+\left(\mathrm{gx}_1+\mathrm{gy}_1+\mathrm{c}\right)=0 \\
\Rightarrow & x_1 \times 0+y_1 \times 0+g x_1+f y_1+c=0 & [\mathrm{Using}(\mathrm{i}) \text { and (ii })] \\
\Rightarrow & g x_1+f y_1+c=0 & \ldots \ldots \ldots \text { (iv) }
\end{array}
$

Solving (i) and (ii) by cross-multiplication, we get $\mathrm{x}_1=\frac{\mathrm{hf}-\mathrm{bg}}{\mathrm{ab}-\mathrm{h}^2} \quad, \quad \mathrm{y}_1=\frac{\mathrm{hg}-\mathrm{af}}{\mathrm{ab}-\mathrm{h}^2}$
The origin must be shifted at $\left(\frac{h f-b g}{a b-h^2}, \frac{h g-a f}{a b-h^2}\right)$
Hence, the answer is $\left(\frac{h f-b g}{a b-h^2}, \frac{h g-a f}{a b-h^2}\right)$

Example 4: If the lines represented by $x^2-2 p x y-y^2=0$ are rotated about the origin through an angle $\theta$, one in the clockwise direction and the other in an anti-clockwise direction, find the equation of the bisectors of the angle between the lines in the new position.

Solution: The bisectors of the angles between the lines in the new position are the same as the bisectors of the angles between their old positions. Therefore, the required equation is

$
\frac{x^2-y^2}{1-(-1)}=\frac{x y}{-p} \Rightarrow-p x^2-2 x y+p y^2=0
$

Hence, the answer is $-\mathrm{px}^2-2 \mathrm{xy}+\mathrm{py}^2=0$

Example 5: The coordinate axes are rotated about the origin $(0,0)$ in counterclockwise direction through an angle of $60^{\circ}$. If p and q are intercepts made on new axes by a straight line whose equation referred to the original axes is $\mathrm{x}+\mathrm{y}=1$, then $\frac{1}{\mathrm{p}^2}+\frac{1}{\mathrm{q}^2}=$
Solution:

When axes are rotated through $60^{\circ}$, co-ordinates are
$
\begin{aligned}
& x=x \cos \theta-y \sin \theta=\frac{x}{2}-\frac{y \sqrt{3}}{2} \\
& y=x \sin \theta-y \cos \theta=\frac{x \sqrt{3}}{2}-\frac{y}{2} \\
& \therefore x+y=1 \Rightarrow \frac{x}{2}-\frac{y \sqrt{3}}{2}+\frac{x \sqrt{3}}{2}+\frac{y}{2}=1 \\
& x \frac{(1+\sqrt{3})}{2}+y \frac{(1-\sqrt{3})}{2}=1 \\
& p=\frac{2}{1+\sqrt{3}} ; q=\frac{2}{1-\sqrt{3}} \\
& \frac{1}{p^2}=\frac{1+3+2 \sqrt{3}}{4} ; \frac{1}{q^2}=\frac{1+3-2 \sqrt{3}}{4} \\
& \therefore \frac{1}{p^2}+\frac{1}{q^2}=\frac{4+4}{4}=2
\end{aligned}
$

If the axes are rotated through $60^{\circ}$, find the $X Y$-coordinates of the point whose $x y$-coordinates are $(2,6)$.
Using Equations with $x=2, y=6$, and $\theta=60^{\circ}$, we have
$
\begin{aligned}
& X=2 \cos 60^{\circ}+6 \sin 60^{\circ}=1+3 \sqrt{3} \\
& Y=-2 \sin 60^{\circ}+6 \cos 60^{\circ}=-\sqrt{3}+3
\end{aligned}
$

The $X Y$-coordinates are $(1+3 \sqrt{3}, 3-\sqrt{3})$.

Summary

The rotation of axes about the origin simplifies the representation and solution of geometric problems. This concept enhances our understanding of coordinate geometry and has practical applications in various fields including engineering, physics, and computer graphics. Mastering the concept helps us to solve various real-life problems.