Addition Of Vectors - Formula, Property, Component

Edited By Team Careers360 | Updated on Jul 02, 2025 05:09 PM IST

The addition of vectors means putting two or more vectors with each other. In the addition of vectors, we are generally adding two or more vectors by using the mathematical operation of addition to obtaining a new length of the vector that is equal to the sum of two or more vectors. It is necessary for the students to understand all the properties of vectors carefully before they read about how to execute any mathematical operation with the vectors. Vectors can be used to do a large number of mathematical operations, addition is one of these operations. This way of adding two or more vectors is more competitive than scalar addition.

This Story also Contains

Details About Addition of Vectors And Vector Addition Formula
Necessary Conditions For The Addition Of Vectors
Important Properties Of Vector Addition And Vector Addition Formula
Vector Addition Formula
Or
Laws Of Addition Of Vectors

Addition Of Vectors - Formula, Property, Component

As an example, If an object completes one complete revolution on a circular path perimeter of eighty miles then the total distance covered by an object is eighty miles. Whereas, there is not any displacement of an object. Now, let us know more about the addition of vectors and important details about the addition of vectors.

Details About Addition of Vectors And Vector Addition Formula

The vectors are always written with an alphabet and with an arrow over them and they are represented as a combination of direction and magnitude. The operation of adding two or more vectors together to form a new vector by using a sum is known as the addition of vectors. The addition of vectors can be completed by using two ways, either by using the triangle law or the parallelogram law.

The two vectors having the same direction, then the sum of their magnitudes will be in the same direction and is always equal to the magnitude of their resultant vector.
If the two vectors are in opposite directions to each other, then the magnitude of the resultant vector of these vectors is the difference of magnitude between these two vectors and the resultant vector’s direction is in the direction of a greater vector.
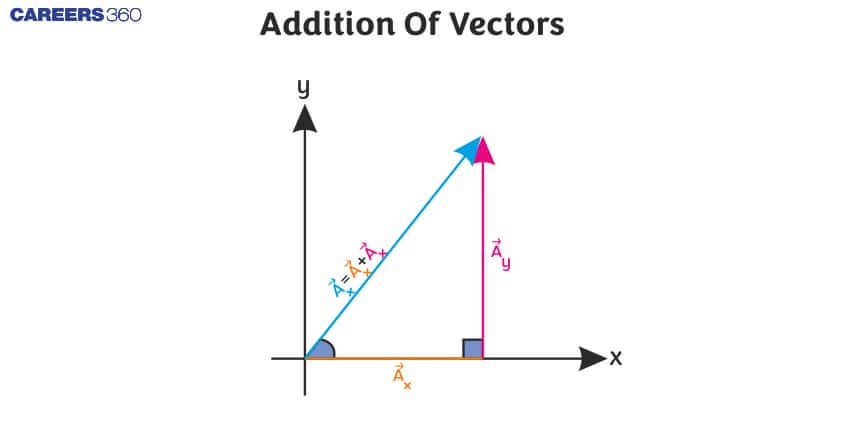
By using vector addition, if two vectors, \vec{x} 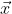and \vec{y} 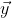have been added together, then their resultant vector can be expressed as \vec{R}= \vec{x}+ \vec{y}.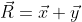

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Necessary Conditions For The Addition Of Vectors

The necessary conditions for the addition of vectors are given as follows:-

1. Only vectors of the same kind can be added together. For example, the acceleration should be added only with the acceleration and not with the displacement.

2. We can not be able to add any vectors with any of the scalars, i.e. we can not add 5 with vector \vec{x}.

Important Properties Of Vector Addition And Vector Addition Formula

The addition of the vectors is fully different from the addition of numbers/scalars. There are the important properties which should be seriously considered during adding vectors:

1. Addition of vectors is always commutative which means that the order of vectors never affects the addition, i.e., If there are two vectors \vec{x} and \vec{y} and they are added together, then \vec{x}+ \vec{y}=\vec{y}+ \vec{x}.

2. The addition of vectors is also always associative which means that the mutual grouping of two or more vectors does not have any effect on the result when three or more vectors are added together, For example,

( \vec{x}+ \vec{y})+\vec{z}=\vec{x}+ (\vec{y}+\vec{z}) .

3. The vector addition is always distributive which means that the scalar times of the sum of any two vectors are equal to the sum of the scalar times of these two vectors individually, For example,

m ( \vec{x}+ \vec{y}) =m\vec{x}+ m \vec{y} .

4. Vector addition always satisfies the Existence of Identity property in which for a vector \vec{x}, \vec{x}+ \vec{0} = \vec{x} .

So, here \vec{0} is the additive identity of \vec{x}.

5. Vector addition has the Existence of inverse means that for any vector \vec{x}, \vec{x} + (-\vec{x}) = \vec{0} .

Hence, an additive inverse exists and -\vec{x} is the additive inverse of \vec{x}.

Vector Addition Formula

Or

Laws Of Addition Of Vectors

For the addition of vectors, there are three important formulas or laws or rules which are as follows :

1. Triangle law for addition of vectors:-

The triangle law for the addition of vectors states that if two vectors are represented such as any two sides of a triangle having the same order of magnitude and direction then the direction and magnitude of the resultant vector are denoted by the third side of that triangle.

Let a triangle PQR, such that

PQ= \vec{x} and QR= \vec{y} , then the resultant side RP= \vec{x} + \vec{y}.

If x= magnitude of \vec{x}

y= magnitude of \vec{y}

θ= angle between \vec{x} and \vec{y}

Then, the magnitude of \vec{x} + \vec{y}

is given by using the formula:- \sqrt{\mathrm{x}^2+\mathrm{y}^2+2\mathrm{x}\mathrm{y} \ Cos \theta } .

2. Parallelogram law for the addition of vectors:-

According to the Parallelogram law for the addition of vectors, if two vectors are represented as two adjacent sides of a parallelogram, both vectors should be pointing away from that common vertex then the resultant vector is denoted by the diagonal of that parallelogram passing through that same common vertex.

Here, PQ= \vec{x} and PS= \vec{y} are represented as the two adjacent sides of a parallelogram PQRS, and then their resultant vector is given by the diagonal PR of the parallelogram PQRS which originates through the same common vertex P.

3. Polygon Law of addition of vectors:-

According to the polygon law, if the number of vectors is represented in direction and magnitude as the sides of a polygon that are taken in the same order, then their resultant vector is represented by direction and magnitude such as the closing side of that polygon is taken in the opposite direction.

Frequently Asked Questions (FAQs)

1. What occurs if two vectors having the same magnitude but opposite in direction are added?

If two vectors having the same magnitude but opposite in direction are added then their resultant vector will be zero.

2. Is the addition of two vectors commutative?

Yes, the addition of two vectors is always commutative.

3. Mention all the laws of the Addition of Vectors.

There are three laws of vectors addition which are given as follows:-

Triangle Law
Parallelogram Law
Polygon Law.

4. What is the condition when the sum of two vectors is maximum?

The sum of two vectors is maximum when both vectors are in the same direction.

5. What are the properties of the addition of vectors?

The addition of vectors holds some properties which are as follows:-

Commutative property
Associative property
Distributive property
Existence of identity
Existence of inverse.

6. What is the importance of vector addition in calculating displacement?

Vector addition is crucial in calculating displacement because displacement is a vector quantity representing the shortest distance between start and end points. When an object moves along a complex path, each segment of the journey can be represented as a vector. The vector sum of these individual displacements gives the total displacement, which may be different from the total distance traveled.

7. How do you add more than two vectors?

To add more than two vectors, you can use either the tip-to-tail method extended to multiple vectors, or the component method. In the tip-to-tail method, continue adding vectors one after another. In the component method, sum all x-components, all y-components (and z-components if in 3D), then combine these sums to find the resultant. Both methods will yield the same result.

8. What is the difference between the algebraic and geometric methods of vector addition?

The algebraic method involves adding the components of vectors numerically, while the geometric method involves graphical representation. The algebraic method is more precise and better for complex calculations, while the geometric method provides a visual understanding and is useful for quick estimations. Both methods are based on the same principles and yield equivalent results.

9. How does the angle between vectors affect their sum?

The angle between vectors significantly affects their sum. When vectors are parallel (0° angle), their magnitudes add directly. As the angle increases, the magnitude of the resultant decreases, reaching a minimum when vectors are antiparallel (180° angle). For perpendicular vectors (90° angle), the Pythagorean theorem is used to find the resultant magnitude.

10. How does vector addition apply to velocity problems?

In velocity problems, vector addition is used to determine resultant velocities. For example, when calculating the velocity of a boat crossing a river, you add the boat's velocity relative to the water (as one vector) to the water's velocity relative to the shore (as another vector). The vector sum gives the boat's actual velocity relative to the shore.

11. What is the associative property of vector addition?

The associative property of vector addition states that the grouping of vectors in addition does not affect the result. Mathematically, it's expressed as (A + B) + C = A + (B + C), where A, B, and C are vectors. This property allows flexibility in the order of adding multiple vectors without changing the final result.

12. What is the null vector, and how does it affect vector addition?

The null vector, also called the zero vector, is a vector with zero magnitude and undefined direction. When added to any other vector, it does not change the original vector. Mathematically, for any vector A, A + 0 = A, where 0 represents the null vector. It acts as the additive identity in vector operations.

13. How does scalar multiplication affect vector addition?

Scalar multiplication scales the magnitude of a vector without changing its direction. When a scalar k multiplies a vector A, it affects vector addition as follows: k(A + B) = kA + kB. This distributive property allows for factoring out common scalars in vector addition problems.

14. What is the triangle inequality theorem in vector addition?

The triangle inequality theorem states that the magnitude of the sum of two vectors is always less than or equal to the sum of the magnitudes of the individual vectors. Mathematically, |A + B| ≤ |A| + |B|. This theorem highlights that vector addition is not simply about adding magnitudes, as the directions of vectors influence the resultant.

15. What is the physical significance of vector addition in force problems?

In force problems, vector addition is crucial for determining the net force acting on an object. Multiple forces acting on a body are represented as vectors, and their vector sum gives the resultant force. This resultant force determines the object's acceleration according to Newton's Second Law of Motion, making vector addition fundamental in analyzing physical systems.

16. How do you add two vectors graphically?

To add vectors graphically, draw the first vector, then draw the second vector starting from the tip of the first vector. The resultant vector is drawn from the tail of the first vector to the tip of the second vector. This method is called the tip-to-tail method or triangle method of vector addition.

17. What is the difference between scalar addition and vector addition?

Scalar addition involves simply adding the magnitudes of quantities, while vector addition takes into account both magnitude and direction. In vector addition, the resultant vector depends on the relative directions of the vectors being added, not just their magnitudes.

18. What is the commutative property of vector addition?

The commutative property of vector addition states that the order in which vectors are added does not affect the result. Mathematically, it's expressed as A + B = B + A, where A and B are vectors. This property holds true for both graphical and algebraic methods of vector addition.

19. How does the parallelogram method of vector addition work?

In the parallelogram method, two vectors to be added are drawn from a common origin. A parallelogram is then constructed using these vectors as adjacent sides. The diagonal of this parallelogram, drawn from the common origin, represents the resultant vector. This method gives the same result as the tip-to-tail method.

20. What is the component method of vector addition?

The component method involves breaking down each vector into its x and y components. The x-components of all vectors are added separately, as are the y-components. The resultant vector is then determined by combining these summed components. This method is particularly useful when dealing with multiple vectors or when precise calculations are needed.

21. Can you add vectors with different units?

No, you cannot add vectors with different units. Just like scalar quantities, vectors can only be added if they represent the same physical quantity and have the same units. For example, you can add two velocity vectors, but you cannot add a velocity vector to a force vector.

22. What is the role of vector addition in understanding projectile motion?

In projectile motion, vector addition is essential for analyzing the object's motion. The initial velocity vector is decomposed into horizontal and vertical components. These components are then treated separately: the horizontal component remains constant (neglecting air resistance), while the vertical component changes due to gravity. Vector addition of these changing components at any given time determines the projectile's instantaneous velocity and trajectory.

23. How does vector addition relate to the concept of equilibrium in physics?

In physics, equilibrium occurs when the net force acting on an object is zero. This is directly related to vector addition: if all forces acting on an object (represented as vectors) sum to zero, the object is in equilibrium. This concept is crucial in statics, where systems remain at rest or in uniform motion due to balanced forces.

24. What is the importance of vector addition in understanding circular motion?

Vector addition is crucial in understanding circular motion, particularly in analyzing centripetal acceleration. The velocity vector in circular motion constantly changes direction, and the addition of small changes in velocity over time results in a net acceleration towards the center of the circle. This centripetal acceleration is perpendicular to the velocity at every point.

25. What is a vector in physics?

A vector is a quantity that has both magnitude and direction. Unlike scalars which only have magnitude, vectors are used to represent physical quantities like displacement, velocity, and force that require both a size and a direction to be fully described.

26. How do you find the magnitude of a resultant vector?

The magnitude of a resultant vector can be found using the Pythagorean theorem if you know its x and y components. If R is the resultant vector with components Rx and Ry, its magnitude |R| is given by: |R| = √(Rx² + Ry²). For more than two vectors, sum all x-components and all y-components first, then apply this formula.

27. What is the significance of the angle in vector addition?

The angle between vectors is crucial in vector addition as it determines how the vectors combine. Vectors pointing in the same direction add to give a larger resultant, while vectors pointing in opposite directions partially cancel out. The angle affects both the magnitude and direction of the resultant vector.

28. How does vector addition in three dimensions differ from two dimensions?

Vector addition in three dimensions follows the same principles as in two dimensions, but includes a third component (z-axis). While 2D vectors are represented by x and y components, 3D vectors have x, y, and z components. The resultant vector in 3D space is calculated by adding corresponding components and can be visualized as the diagonal of a rectangular cuboid.

29. How do unit vectors simplify vector addition?

Unit vectors are vectors with a magnitude of 1 and are typically denoted as î, ĵ, and k̂ for the x, y, and z directions respectively. They simplify vector addition by allowing any vector to be expressed as a sum of its components multiplied by these unit vectors. For example, A = Axî + Ayĵ + Azk̂. This makes it easier to perform vector calculations algebraically.

30. How does vector subtraction relate to vector addition?

Vector subtraction is essentially vector addition with a negative vector. To subtract vector B from vector A, you add the negative of B to A. Mathematically, A - B = A + (-B). Graphically, this is equivalent to reversing the direction of the vector being subtracted before adding it using the tip-to-tail method.

31. What is meant by the term "vector resolution"?

Vector resolution is the process of breaking down a single vector into two or more component vectors, typically along perpendicular axes. This is the opposite of vector addition and is useful for analyzing forces in different directions or simplifying complex vector problems into manageable components.

32. Can the magnitude of a resultant vector be less than the magnitude of one of its components?

Yes, the magnitude of a resultant vector can be less than the magnitude of one of its components. This occurs when vectors are pointing in nearly opposite directions, causing partial cancellation. For example, when adding two vectors of similar magnitude pointing in opposite directions, the resultant vector will be smaller than either of the original vectors.

33. How do you determine the direction of a resultant vector after addition?

The direction of a resultant vector can be determined by calculating the angle it makes with one of the coordinate axes, typically the x-axis. If Rx and Ry are the x and y components of the resultant vector, the angle θ is given by θ = tan⁻¹(Ry/Rx). The quadrant of the angle is determined by the signs of Rx and Ry.

34. What is the significance of the parallelogram law in vector addition?

The parallelogram law is a fundamental principle in vector addition, stating that the sum of two vectors is represented by the diagonal of the parallelogram formed by the vectors. This law provides a geometric interpretation of vector addition and forms the basis for both the parallelogram method and the triangle method of vector addition.

35. How does vector addition apply to wave interference?

In wave interference, vector addition is used to determine the resultant amplitude when two or more waves overlap. The displacement vectors of individual waves at each point are added vectorially. This can result in constructive interference (where waves reinforce each other) or destructive interference (where waves cancel out), depending on the phase relationship between the waves.

36. What is the relationship between vector addition and the superposition principle?

The superposition principle, which states that the net response caused by multiple stimuli is the sum of the responses caused by each stimulus individually, is fundamentally a principle of vector addition. In physics, this applies to various phenomena like forces, electric fields, and wave displacements, where the total effect is the vector sum of individual effects.

37. How does vector addition help in understanding momentum conservation?

Vector addition is essential in understanding momentum conservation. In collisions or interactions between objects, the total momentum before and after the event must be conserved. This conservation is expressed as a vector equation, where the vector sum of momenta before the collision equals the vector sum of momenta after, taking into account both magnitude and direction.

38. What role does vector addition play in analyzing torque?

Vector addition is crucial in analyzing torque, which is a vector quantity. When multiple forces act on an object causing rotation, the net torque is determined by the vector sum of individual torques. This is important in understanding rotational dynamics and equilibrium in systems where multiple forces act at different points or angles.

39. How is vector addition used in electromagnetic theory?

In electromagnetic theory, vector addition is used extensively. Electric and magnetic fields are vector quantities, and the net field at any point is the vector sum of all contributing fields. This principle is applied in calculating resultant electric fields from multiple charges, or magnetic fields from multiple current-carrying wires.

40. What is the significance of vector addition in understanding relative motion?

Vector addition is fundamental in analyzing relative motion. When an object moves relative to a moving reference frame, its observed velocity is the vector sum of its velocity relative to the moving frame and the frame's velocity relative to a stationary observer. This concept is crucial in problems involving motion on moving platforms or in fluid flows.

41. How does vector addition apply to the concept of work in physics?

In physics, work is defined as the dot product of force and displacement vectors. When multiple forces act on an object, vector addition is used to find the net force before calculating work. Additionally, for a complex path, the total work done is the sum of work done over each segment, which involves vector addition of displacement segments.

42. What is the importance of vector addition in analyzing magnetic force?

Vector addition is crucial in analyzing magnetic force, which acts perpendicular to both the magnetic field and the velocity of a charged particle. The resultant force on a charged particle moving in a magnetic field is determined by the vector cross product of velocity and magnetic field vectors. In complex magnetic fields, the net force is the vector sum of forces from each field component.

43. How does vector addition help in understanding the concept of mechanical advantage in simple machines?

Vector addition helps in analyzing the forces in simple machines like levers and pulleys. The mechanical advantage is often a result of how forces are redirected and combined. By representing forces as vectors and using vector addition, we can understand how a small input force can result in a larger output force, or how force direction changes in these systems.

44. What is the role of vector addition in analyzing fluid dynamics?

In fluid dynamics, vector addition is essential for understanding concepts like fluid velocity and pressure gradients. The velocity of a fluid particle can be represented as a vector, and the flow field is described by vector addition of these velocities. Similarly, pressure forces in different directions are analyzed using vector addition to determine net forces on objects in fluids.

45. How is vector addition applied in the analysis of electric circuits?

In electric circuits, vector addition is used particularly when dealing with alternating current (AC) circuits. Voltages and currents in AC circuits are represented as phasors, which are rotating vectors. The analysis of complex circuits often involves adding these phasor quantities vectorially to determine net voltages or currents, taking into account both magnitude and phase.

46. What is the significance of vector addition in understanding optical phenomena?

Vector addition is crucial in optics, especially in understanding wave optics and polarization. Light waves are described by electric field vectors, and the interaction of light with various media involves the vector addition of these fields. This is particularly important in analyzing phenomena like interference, diffraction, and the behavior of polarized light.

47. How does vector addition contribute to the analysis of quantum mechanics?

In quantum mechanics, vector addition plays a role in the concept of superposition of states. Quantum states can be represented as vectors in a complex vector space, and the principle of superposition states that any linear combination (vector sum) of valid quantum states is also a valid quantum state. This fundamental principle underlies many quantum phenomena.

48. What is the importance of vector addition in analyzing satellite orbits?

Vector addition is essential in analyzing satellite orbits. The motion of a satellite is determined by the vector sum of gravitational forces from various bodies (like the Earth, Moon, and Sun) and other forces like solar radiation pressure. Additionally, orbital maneuvers are calculated using vector addition of velocity changes to determine new orbital paths.

49. How is vector addition used in weather forecasting and atmospheric science?

In meteorology, vector addition is crucial for analyzing wind patterns and atmospheric circulation. Wind velocity is a vector quantity, and the movement of air masses is often the result of vector addition of various forces and velocities. This includes the analysis of geostrophic winds, where the wind velocity is a balance of pressure gradient and Coriolis forces.

50. What role does vector addition play in understanding the behavior of plasmas?

In plasma physics, vector addition is fundamental in analyzing the motion of charged particles under the influence of electric and magnetic fields. The Lorentz force, which determines the motion of charged particles in plasmas, is calculated using vector addition of electric and magnetic force components. This is crucial in studying phenomena like fusion reactions and astrophysical plasmas.

51. How does vector addition apply to the analysis of stress and strain in materials?

In materials science and engineering, vector addition is used to analyze stress and strain in materials. Stress and strain are tensor quantities that can be represented as vectors in different directions. The total stress or strain in a material under complex loading conditions is determined by the vector sum of individual stress or strain components.

52. What is the significance of vector addition in understanding the Doppler effect?

Vector addition is important in analyzing the Doppler effect, especially in scenarios