Position and Displacement Vectors

Position and Displacement Vectors - A Complete Guide

Edited By Vishal kumar | Updated on Jul 02, 2025 05:01 PM IST

A vector may be an extent that has both magnitude and direction. Vectors allow us to explain the quantities which have both direction and magnitude. For instance velocity, and position. In this article we will discuss about, what is Position? Or definition of position. What is position vector? Define position vector with its formula. How to find Position vector? How can we describe the position of an object? What is displacement vector? Give its formula. We define the position vector as a straight-line possessing one end fixed to an object and therefore the other end attached to a moving point (marked by an arrowhead) and wont to represent the position of the purpose relative to the given object. Since, the point moves, the position vector switches long or in direction, and sometimes both length and direction changes. Are you know, what is Position??? So Now We define Position (Edge) is that the location of the thing (whether it is a person, a ball, or a particle) at a given moment in time. Vector physics vallah is anything which also has direction. A displacement vector is an idea from vectors. It’s a vector. It indicates the direction and distance traveled with a line.

Position and Displacement Vectors - A Complete Guide

Also check-

What is Position Vector?

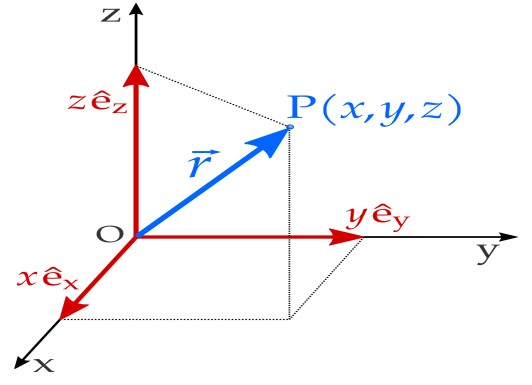
A position or edge(Position) vector, also known as location vector or radius vector, is a Euclidean vector that represents the position of a point P in space in relation to an arbitrary reference origin O. Usually signified as x, r, or s, it point to the straight line segment from O to P.

Radius vector r represent the postion of point P (x, y, z) with repect to origin O

In the above statement, we took a frame of reference to represent your journey from the origin, i.e., your home to succeed in your favorite destinations, first, Tamilnadu, then, Bengluru.
Each destination is marked by an arrow on the graph, which changes or varies as you modify your destination, below represent the same:

Hence, your position vector changes, i.e., twice or twice the length,
So, along the X-axis, the position vector is: ‘i (cap)’ and along the Y-axis, it's ‘j (cap)’. Since the position resultant is represented by r→
, therefore the resultant of the position vectors along with coordinate axes are going to be as follows:

r→ + I (cap) + j (cap) ……………………… (1)

Now In these Articles, the points we have to discuss about Position Vector are:

Explain what's an edge (Position) Vector?
And how to find out the Position Vector?
How can we describe the position of an object?

Often, we've noticed that the vectors start at the origin and terminate at any arbitrary point are referred to as position vectors. These are said to work out the position of some extent with regard to the origin of that time. The orientation/direction of the vectors or the position vector generally points from the origin towards the given point. Within the frame of reference of c\Cartesian if point O is that the origin and Q is a few points that's x1, y1, then the directed position vector from point O to point Q is identified as OQ. Within the space which is three-dimensional if O = (0, 0, and 0) and Q = (x1, y1, z1), then the position vector denoted by r of point Q is represented is:

r = x1i + y1j + z1k

Now let’s suppose that we've two vectors, that are A and B, with position vectors we write a = (2, 4) and b = (3, 5) respectively. We will then write the coordinates of both the vectors that are A and B as:

A = (2, 4), B = (3, 5)

Here before determining the position vector of some extent we first got to determine the coordinates of these particular points. Let’s suppose that we've two points, namely M and N. where the purpose M = (x1, y1) and N = (x2, y2). Next we would like to seek out here the position vector that too from point M to point N the vector MN. To work out this position vector, we simply subtract the corresponding components of M from N:

Written as: MN = (x2-x1, y2-y1)

Related Topics Link,

Position Vector Formula:

If we consider some extent denoted by letter P. Which has the coordinates that are xk, yk within the xy-plane and another point written as Q. Which has the coordinates denoted by xk+1, yk+1.

The formula which is to work out the position vector that's from P to Q is written as:

PQ = ((xk+1)-xk, (yk+1)-yk)

We can now remember the position vector that's PQ which generally refers to a vector that starts at the purpose P and ends at the purpose Q. Similarly if we would like to findout the position vector that's from the purpose Q to the purpose P then we will write:

QP = (xk – (xk+1), yk – (yk+1))

How can we describe the position of an object?

The changes in position of an object with reference to its surroundings during a given interval of your time. An object is moving if its position relative to a hard and fast point is changing. Even things that indicate to be at rest move.

Also Read:

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Displacement Vector

The change within the position vector of an object is understood because the displacement vector. Let us consider an object is at point A at time = 0 and at point B at time = t. The position vectors of the thing at point A and at point B are given as:

Position vector at point A = r^A = 5 i^ + 3 j^+ 4 k^
Position vector at point B = r^B = 2 i^ + 2 j^+ 1 k^
Now, the displacement vector of the thing from interval 0 to t will be:
r^A - r^B = - 3 i^ - j^+ 3k^
The displacement of an object also can be defined because the vector distance between the initial point and therefore the final point. Suppose an object travels from point A to point B within the path shown within the black curve:

The displacement of the particle would be the vector line AB, lead inside the direction A to B. The direction of the displacement vector is usually headed from the initial point to the ultimate point.

Also read -

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

1. Explain Can an edge(Position) Vector be Negative?

If there are two vectors that are having an equivalent magnitude that's size and therefore the same direction also. Then we will generally call them adequate to one another. A bit like the scalars which may have negative or the positive values. The vectors also can be negative or positive. A vector which is that the negative may be a vector which points within the direction opposite to the reference positive direction.

2. What is meant by Fixed Vector?

Fixed vector is that vector whose initial point or tail is fixed. It's also referred to as localised vector. For instance, The initial point of an edge(position) vector is fixed at the origin of the coordinate axes. So, position vector may be a fixed or localized vector.

3. Explain what's the Position and Displacement Vector?

The vector which is that the position vector is employed to specify the position of a particular body. The term displacement vector is employed to seek out the change that's within the position vector of an object. The vector which generally represents the position of an object and therefore the origin because the frame of reference is understood as position vector.

4. What is the meaning of position vector?

Position vector, line having one end fixed to a body and therefore the other end attached to a moving point and wont to describe the position of the purpose relative to the body.

5. What is the difference between position and displacement vectors?

Position vectors indicate an object's location relative to a fixed origin, while displacement vectors represent the change in position between two points. Position vectors give absolute location, while displacement vectors show relative movement.

6. Why is displacement considered a vector quantity?

Displacement is a vector quantity because it has both magnitude and direction. It represents not just how far an object has moved, but also in which direction, making it fundamentally different from scalar quantities like distance.

7. Can displacement be greater than the total distance traveled?

No, displacement cannot be greater than the total distance traveled. Displacement is the straight-line distance between start and end points, while total distance includes all path lengths. The displacement is always less than or equal to the total distance.

8. How do you add displacement vectors?

Displacement vectors are added using vector addition, typically through the tip-to-tail method or component method. This involves considering both magnitude and direction, not simply adding scalar values.

9. Can displacement be zero even if an object has moved?

Yes, displacement can be zero even if an object has moved. This occurs when the object returns to its starting point. The total distance traveled may be non-zero, but the net displacement (straight-line distance between start and end points) is zero.

10. How does the concept of reference frame relate to position vectors?

A reference frame is crucial for position vectors as it provides the origin and coordinate system for measuring position. The same object can have different position vectors in different reference frames, highlighting the importance of specifying the frame when discussing position.

11. How does dimensional analysis apply to position and displacement vectors?

Both position and displacement vectors have the dimension of length [L]. This is important for checking the consistency of equations and ensuring that physical quantities are correctly related in formulas involving these vectors.

12. How do position and displacement vectors behave in circular motion?

In circular motion, the position vector continuously changes as the object moves around the circle. However, the displacement vector can vary depending on the time interval considered. For a complete revolution, the displacement is zero, despite the changing position.

13. How do position and displacement vectors relate to coordinate systems?

Position and displacement vectors are typically expressed in terms of coordinate systems (e.g., Cartesian, polar). The choice of coordinate system can simplify calculations and affect how the vectors are represented, but doesn't change their physical meaning.

14. Can an object have a changing position vector but constant displacement vector?

No, if an object's position vector is changing, its displacement vector must also change. Displacement represents the change in position, so any alteration in position necessarily affects the displacement vector.

15. What's the relationship between velocity and displacement vectors?

Velocity is the rate of change of displacement with respect to time. Mathematically, average velocity is the displacement vector divided by the time interval. Instantaneous velocity is the limit of this ratio as the time interval approaches zero.

16. How does a position-time graph relate to displacement?

In a position-time graph, displacement is represented by the vertical change between two points. The slope of the line connecting these points gives the average velocity, showing the intimate relationship between position, displacement, and velocity.

17. Can you have a non-zero displacement with zero net force?

Yes, you can have a non-zero displacement with zero net force. This occurs in situations of constant velocity motion, where an object continues moving due to inertia without any net force acting on it, resulting in a changing position and non-zero displacement.

18. What's the relationship between displacement and the concept of free body diagrams?

While displacement itself isn't typically shown in free body diagrams, understanding displacement is crucial for analyzing the forces in these diagrams. The net force in a free body diagram determines how an object's displacement will change over time.

19. Can displacement be used to determine average speed?

No, displacement alone cannot determine average speed. Average speed is calculated using the total distance traveled, not displacement. This highlights the difference between vector quantities (like displacement) and scalar quantities (like distance and speed).

20. How do position and displacement vectors relate to the concept of relative velocity?

Relative velocity is the velocity of an object as observed from a moving reference frame. It can be calculated using the displacement vectors of both the object and the moving frame, highlighting the interconnected nature of these concepts.

21. What's the relationship between displacement and the concept of work-energy theorem?

The work-energy theorem relates the work done on an object to its change in kinetic energy. Displacement is crucial here, as work is calculated using the displacement vector, not the total distance traveled, emphasizing again the vector nature of these concepts.

22. How do position and displacement vectors relate to the concept of momentum?

While position and displacement vectors don't directly appear in the formula for momentum (p = mv), they're crucial for understanding how momentum changes. The change in momentum over time is related to the displacement of an object, connecting these concepts.

23. Can displacement be used to determine if motion is linear?

Displacement alone cannot determine if motion is linear. Linear motion implies constant direction, which requires comparing multiple displacement vectors over time. If all displacement vectors over different time intervals are parallel, the motion is linear.

24. What's the relationship between displacement and the concept of impulse?

While displacement isn't directly used in calculating impulse, understanding displacement is crucial for analyzing the effects of impulse. An impulse causes a change in momentum, which results in a displacement of the object over time.

25. Can displacement be used to determine if a system is in equilibrium?

A non-zero displacement doesn't necessarily mean a system isn't in equilibrium. However, if a system in equilibrium is displaced and then released, it should return to its original position. The study of such displacements is key in analyzing stable and unstable equilibria.

26. Why is it important to specify the time interval when discussing displacement?

Specifying the time interval is crucial because displacement can vary significantly over different time periods. Without a defined interval, it's impossible to accurately describe an object's motion or calculate related quantities like velocity.

27. What's the significance of the negative sign in a displacement vector?

A negative sign in a displacement vector indicates direction. It shows that the object has moved in the opposite direction to the positive reference axis. This highlights the vector nature of displacement, where both magnitude and direction are essential.

28. What's the difference between average and instantaneous displacement?

Average displacement is calculated over a finite time interval and represents the overall change in position. Instantaneous displacement is the limit of average displacement as the time interval approaches zero, effectively giving the displacement at a specific moment.

29. Can displacement be used to determine the actual path of an object?

No, displacement alone cannot determine the actual path of an object. It only provides information about the start and end points. To know the actual path, you need additional information about the object's motion between these points.

30. How does the concept of relative motion apply to displacement vectors?

Relative motion affects displacement vectors because displacement depends on the observer's frame of reference. The same motion can result in different displacement vectors when viewed from different reference frames, emphasizing the relative nature of motion.

31. What's the relationship between position vectors and trajectory?

A trajectory is the path that a moving object follows through space. It can be described by a series of position vectors over time. While each position vector gives a snapshot of location, the full set of vectors defines the trajectory.

32. How do position and displacement vectors behave in accelerated motion?

In accelerated motion, the rate of change of the position vector (velocity) is not constant. This results in a non-linear relationship between time and displacement. The displacement vector changes non-uniformly, reflecting the varying velocity.

33. How do unit vectors relate to position and displacement vectors?

Unit vectors are vectors with a magnitude of 1 that indicate direction. They're used to express position and displacement vectors in component form. For example, in 3D space, position and displacement can be written as combinations of unit vectors i, j, and k.

34. What's the significance of the origin in defining position vectors?

The origin is crucial in defining position vectors as it serves as the reference point from which all positions are measured. Changing the origin will change all position vectors, but it won't affect displacement vectors between two points.

35. How do position and displacement vectors behave in projectile motion?

In projectile motion, the position vector changes continuously in both horizontal and vertical components. The displacement vector represents the straight-line change between any two points on the trajectory, not the curved path the projectile actually follows.

36. Can displacement be used to calculate work done?

Yes, displacement is used to calculate work done by a constant force. Work is defined as the dot product of the force vector and the displacement vector. This highlights the importance of displacement (not distance) in determining the work done by a force.

37. How do position and displacement vectors relate to velocity and acceleration vectors?

Velocity is the rate of change of the position vector with respect to time, or the first derivative of position. Acceleration is the rate of change of the velocity vector, or the second derivative of position. Displacement is the integral of velocity over time.

38. What's the importance of vector components in analyzing position and displacement?

Vector components allow complex motions to be broken down into simpler parts along coordinate axes. This simplifies calculations and analysis, especially in multi-dimensional motion. Components of position and displacement vectors can be treated independently in many situations.

39. How does the principle of superposition apply to displacement vectors?

The principle of superposition states that the net displacement resulting from multiple displacements is the vector sum of the individual displacements. This principle is crucial in analyzing complex motions and in understanding how different motions combine.

40. Can position and displacement vectors be used in rotational motion?

Yes, position and displacement vectors can be used in rotational motion, but they're often expressed in polar or spherical coordinates rather than Cartesian. Angular displacement, a related concept, measures the angle through which an object rotates.

41. How do position and displacement vectors behave in simple harmonic motion?

In simple harmonic motion, the position vector oscillates sinusoidally about an equilibrium point. The displacement vector continuously changes in magnitude and direction, but is always directed towards the equilibrium position.

42. How do position and displacement vectors relate to the concept of frames of reference?

Position and displacement vectors are frame-dependent, meaning their values can change depending on the chosen frame of reference. This is a key concept in relativity and highlights the importance of specifying the reference frame when discussing motion.

43. How do position and displacement vectors behave in uniform circular motion?

In uniform circular motion, the magnitude of the position vector (radius) remains constant, but its direction continuously changes. The displacement vector over one complete revolution is zero, despite the object having traveled a distance equal to the circumference.

44. What's the significance of initial and final position vectors in calculating displacement?

The initial and final position vectors are crucial for calculating displacement. Displacement is found by subtracting the initial position vector from the final position vector. This subtraction accounts for both the magnitude and direction of the movement.

45. Can displacement be negative?

The magnitude of displacement is always positive, but the displacement vector can be negative in the sense that it can point in the negative direction of a coordinate axis. This emphasizes the importance of considering both magnitude and direction in vector quantities.

46. How do position and displacement vectors behave in two-dimensional motion?

In two-dimensional motion, position and displacement vectors have components in two perpendicular directions. The total displacement is the vector sum of these components, often calculated using the Pythagorean theorem and trigonometry.

47. How do position and displacement vectors behave in simple pendulum motion?

In simple pendulum motion, the position vector traces an arc. The displacement vector changes continuously in both magnitude and direction. At the extremes of the swing, the displacement is maximum but momentarily zero velocity.

48. What's the significance of displacement in defining mechanical waves?

In mechanical waves, displacement refers to the distance and direction that a point on the medium moves from its equilibrium position. This concept is fundamental to understanding wave propagation and behavior.

49. How do position and displacement vectors relate to the concept of center of mass?

The center of mass of a system can be represented by a position vector. The displacement of the center of mass is often used to simplify the analysis of complex systems, treating them as single particles in many calculations.

50. Can displacement be used to determine the direction of motion?

Displacement can indicate the overall direction of motion between start and end points, but it doesn't provide information about the path taken or any changes in direction during the motion. It gives the net effect of the motion, not its full history.

51. How do position and displacement vectors behave in damped oscillations?

In damped oscillations, both position and displacement vectors behave similarly to simple harmonic motion, but with decreasing amplitude over time. The displacement vector's magnitude gradually decreases as energy is dissipated from the system.

52. How do position and displacement vectors relate to the concept of torque?

Torque is calculated using the position vector from the axis of rotation to the point where force is applied. While displacement isn't directly used in the torque formula, understanding both position and displacement is crucial for analyzing rotational motion.

53. How do position and displacement vectors behave in fluid dynamics?

In fluid dynamics, position and displacement vectors can describe the motion of individual fluid particles or elements. The concept of displacement fields is used to describe how entire regions of fluid move and deform.

54. What's the significance of displacement in understanding conservation laws?

Displacement plays a crucial role in many conservation laws. For example, in conservative force fields, the work done (which involves displacement) is independent of the path taken, leading to the conservation of mechanical energy. This highlights the fundamental nature of displacement in physics.