Difference between impedance and reactance.

Impedance:- It is the combined opposition of the resistor, inductor and/or capacitor to flow of a.c. in the circuit. Reactance:-The reactance is the opposition offered by an inductor or by a capacitor or by both.

Distinguish between resistance and reactance.

Resistance:-The resistance is the opposition offered by a resistor to the flow of a.c. in a circuit. Reactance:- The reactance is the opposition offered by an inductor or by a capacitor or by both.

The resistance of a coil for direct current is 5Ω. What will be the effect on its resistance when connected in the alternating current circuit?

The resistance will increase. The effective resistance (impedance) for a.c. will be √(R² +(⍵L)²).

What is reactance in AC circuits?

Reactance is the opposition to current flow in AC circuits caused by inductors and capacitors. Unlike resistance, reactance depends on the frequency of the AC signal and doesn't dissipate power as heat.

How does impedance differ from resistance?

Impedance is the total opposition to current flow in AC circuits, combining both resistance and reactance. While resistance is constant for DC and AC, impedance can change with frequency and includes the effects of inductors and capacitors.

Why do we need to consider impedance in AC circuits?

Impedance is crucial in AC circuits because it accounts for both resistive and reactive elements. It helps us understand how current flow is affected by frequency-dependent components like capacitors and inductors, which behave differently than simple resistors.

What is the formula for calculating impedance?

The formula for impedance (Z) is Z = √(R² + X²), where R is resistance and X is reactance. This formula combines the effects of resistance and reactance using the Pythagorean theorem, as they act perpendicular to each other in complex AC circuits.

How does capacitive reactance change with frequency?

Capacitive reactance decreases as frequency increases. This is because capacitors charge and discharge more quickly at higher frequencies, offering less opposition to current flow. The formula for capacitive reactance is Xc = 1 / (2πfC), where f is frequency and C is capacitance.

What happens to inductive reactance as frequency increases?

Inductive reactance increases with frequency. This occurs because the changing magnetic field in inductors opposes current changes more strongly at higher frequencies. The formula for inductive reactance is XL = 2πfL, where f is frequency and L is inductance.

Can impedance ever be zero in an AC circuit?

Yes, impedance can be zero in an AC circuit, but only in special cases. This occurs in a resonant circuit when inductive reactance exactly cancels out capacitive reactance at a specific frequency, leaving only the resistance (which could theoretically be zero in a superconductor).

What is the phase angle in relation to impedance?

The phase angle in impedance represents the difference in timing between voltage and current waveforms in an AC circuit. It's determined by the ratio of reactance to resistance and indicates whether the circuit is more inductive (current lags voltage) or capacitive (current leads voltage).

How does a purely resistive circuit differ from one with reactance in terms of impedance?

In a purely resistive circuit, impedance equals resistance and doesn't change with frequency. The voltage and current are in phase. In circuits with reactance, impedance varies with frequency, and there's a phase difference between voltage and current.

Why is complex notation (j-operator) used to represent impedance?

Complex notation (using the j-operator) is used to represent impedance because it allows us to easily combine resistance (real part) and reactance (imaginary part) in calculations. This notation helps in visualizing the phase relationships and simplifies mathematical operations in AC circuit analysis.

What is the significance of negative reactance?

Negative reactance indicates a capacitive element in the circuit. While inductive reactance is always positive, capacitive reactance is considered negative. This convention helps in calculations and in understanding whether current leads or lags voltage in the circuit.

How does skin effect influence impedance at high frequencies?

Skin effect causes current to flow mainly near the surface of a conductor at high frequencies, effectively reducing the usable cross-sectional area. This increases the AC resistance of the conductor, thereby increasing its impedance at high frequencies.

What is characteristic impedance in transmission lines?

Characteristic impedance is the ratio of voltage to current in a uniform transmission line. It's a constant value determined by the line's physical properties and is crucial for matching impedances to minimize signal reflections in high-frequency applications.

How does temperature affect impedance?

Temperature primarily affects the resistive component of impedance. As temperature increases, the resistance of most materials increases, leading to a change in overall impedance. The reactive components (inductance and capacitance) are generally less affected by temperature.

Can impedance be negative?

While individual components of impedance (like capacitive reactance) can be negative, the overall impedance magnitude is always positive or zero. Negative impedance can exist in active circuits with energy-adding elements, but this is a special case not found in passive components.

What is the relationship between impedance and power factor?

Power factor is related to the phase angle of impedance. A high power factor (close to 1) indicates that impedance is mostly resistive, while a low power factor suggests a significant reactive component. Improving power factor often involves adjusting the reactive elements of impedance.

How does mutual inductance affect the impedance of coupled circuits?

Mutual inductance between coupled circuits can increase or decrease the effective impedance, depending on whether the coupling is additive or subtractive. This effect is crucial in transformers and can significantly alter the behavior of coupled AC circuits.

What is the concept of wave impedance in electromagnetics?

Wave impedance is the ratio of the electric field to the magnetic field in an electromagnetic wave. In free space, this impedance is constant (approximately 377 ohms) and is crucial for understanding wave propagation and reflection at boundaries between different media.

How do parasitic capacitances and inductances affect impedance in high-frequency circuits?

Parasitic capacitances and inductances, which are unintended but unavoidable in real components, can significantly alter impedance at high frequencies. They can create resonances, change the frequency response, and limit the usable frequency range of circuits.

What is the difference between series and parallel impedance?

In series impedance, the total impedance is the sum of individual impedances. In parallel impedance, the reciprocal of total impedance is the sum of reciprocals of individual impedances. This distinction is crucial for analyzing complex AC circuits with multiple components.

How does impedance matching work in audio and RF systems?

Impedance matching in audio and RF systems involves adjusting the source and load impedances to maximize power transfer and minimize signal reflections. This is crucial for efficient energy transfer and maintaining signal integrity in transmission lines and audio equipment.

What is the significance of the complex plane in representing impedance?

The complex plane allows for a visual representation of impedance, with resistance on the real axis and reactance on the imaginary axis. This representation helps in understanding phase relationships and in performing vector operations on impedance values.

How does the quality factor (Q) relate to impedance in resonant circuits?

The quality factor (Q) is related to the sharpness of resonance in a circuit. A high Q indicates a low-loss circuit with a sharp resonance peak, implying a rapid change in impedance near the resonant frequency. Q is defined as the ratio of energy stored to energy dissipated per cycle.

What is the concept of surface impedance in electromagnetic theory?

Surface impedance is the ratio of tangential electric field to surface current density at a material's surface. It's important in analyzing wave propagation in conductors and dielectrics, especially at high frequencies where skin effect becomes significant.

How do distributed impedance elements differ from lumped elements?

Distributed impedance elements, like transmission lines, have their parameters spread out over their length, unlike lumped elements (discrete resistors, capacitors, inductors). This distribution becomes significant when the circuit's physical size is comparable to the wavelength of the signal.

What is the role of impedance in antenna design?

In antenna design, impedance matching between the antenna and its feed line is crucial for efficient power transfer. The antenna's impedance varies with frequency and affects its radiation pattern, efficiency, and bandwidth. Proper impedance matching maximizes the power radiated by the antenna.

How does the concept of impedance apply to acoustic systems?

In acoustics, impedance represents the opposition to the flow of sound energy. Acoustic impedance is crucial in designing speakers, musical instruments, and acoustic spaces. It affects sound transmission, reflection, and absorption, playing a key role in acoustic matching and efficiency.

What is the significance of characteristic impedance in waveguides?

Characteristic impedance in waveguides is crucial for understanding wave propagation and mode behavior. It affects power transmission, reflection coefficients, and mode coupling. Unlike in transmission lines, waveguide impedance can vary with frequency and propagation mode.

How does impedance affect the bandwidth of a circuit?

Impedance variations with frequency can limit a circuit's bandwidth. Circuits with large impedance variations over frequency tend to have narrower bandwidths. Broadband designs often involve techniques to maintain consistent impedance across a wide frequency range.

What is the concept of input impedance in amplifier circuits?

Input impedance in amplifiers is the effective load seen by the signal source. High input impedance minimizes loading effects on the source, preserving signal integrity. It's particularly important in voltage amplifiers and in interfacing different stages of a circuit.

How does the earth's impedance affect grounding systems?

Earth impedance affects the effectiveness of grounding systems, particularly in power distribution and lightning protection. It varies with soil composition, moisture content, and frequency. Low earth impedance is desirable for efficient grounding and safety in electrical systems.

What is the relationship between impedance and standing wave ratio (SWR)?

Standing Wave Ratio (SWR) is directly related to impedance mismatch in transmission lines. A perfect impedance match results in an SWR of 1:1, while mismatches lead to higher SWR values. SWR is a practical measure of how well a load's impedance matches the characteristic impedance of a line.

How does impedance affect the efficiency of power transfer in AC circuits?

Maximum power transfer occurs when the source impedance matches the load impedance. Mismatched impedances result in reduced power transfer efficiency. In AC circuits, both the magnitude and phase of impedance must be considered for optimal power transfer.

What is the concept of wave impedance mismatch in material interfaces?

Wave impedance mismatch at material interfaces causes reflection and transmission of electromagnetic waves. The degree of mismatch determines the amount of energy reflected or transmitted. This concept is crucial in optics, acoustics, and electromagnetic shielding.

What is the role of impedance in electromagnetic compatibility (EMC)?

In EMC, impedance affects how circuits emit and are susceptible to electromagnetic interference. Proper impedance matching and control can reduce emissions and improve immunity. Understanding impedance is crucial for designing EMC-compliant systems and effective shielding.

How does impedance affect the propagation of surface plasmons in nanophotonics?

In nanophotonics, the impedance of metal-dielectric interfaces affects the propagation of surface plasmons. It influences the confinement, propagation length, and coupling efficiency of plasmonic waves, which is crucial for designing nanoscale optical devices and sensors.

What is the concept of mechanical impedance in vibration analysis?

Mechanical impedance in vibration analysis is analogous to electrical impedance. It represents the opposition to motion in mechanical systems, combining the effects of mass, stiffness, and damping. Understanding mechanical impedance is crucial for analyzing and controlling vibrations in structures and machines.

How does impedance affect the performance of RFID systems?

In RFID systems, impedance matching between the antenna and the chip is crucial for efficient power transfer and communication range. Mismatched impedances can significantly reduce the read range and reliability of RFID tags. Proper impedance design is essential for optimizing RFID performance.

What is the significance of impedance in metamaterial design?

In metamaterials, engineered structures with unusual electromagnetic properties, impedance plays a crucial role in determining wave propagation characteristics. Designing specific impedance profiles allows for the creation of materials with negative refractive index, perfect lensing, and cloaking properties.

How does impedance affect the efficiency of wireless power transfer systems?

In wireless power transfer, impedance matching between the transmitter and receiver coils is crucial for maximizing power transfer efficiency. The concept of coupled impedances in resonant systems is used to optimize the transfer of energy across air gaps in applications like wireless charging.

Reactance and Impedance - Definition, Formula, FAQs

Physics
Alternating Current
reactance and impedance

Reactance and Impedance - Definition, Formula, FAQs

Team Careers360Updated on 02 Jul 2025, 05:01 PM IST

Impedance:- impedance meaning (impedance meaning in English) hindrance. Impedance definition ( impedance definition physics ), “It is the combined opposition of the resistor, inductor and/or capacitor to flow of a.c. in the circuit”. Impedance is also known as electrical impedance.

Impedance symbol is the Z. The Impedance unit is the ohm, which is called the impedance because it impedes the flow of alternating current in the circuit. Impedance meaning in Hindi प्रतिबाधा. Impedance meaning in Tamil is மின் தடுப்பு

What is the formula for impedance? Let’s discuss it. The impedance formula or electrical impedance formula in the different circuits is different.

Key points:-

Impedance, impedance meaning, what is impedance (or what is electrical impedance), impedance formula, impedance unit.
Reactance, what is reactance, reactance formula, reactance unit, reactance meaning etc.,
What is admittance, admittance formula, XC meaning.

Also read -

Impedance formula in L-R series circuit:-

i = V/√(R² + X²L)

Applying Ohm's law, we see that √(R² + X²L) is the effective resistance of the circuit. It is called the impedance of the circuit, which is represented by Z. Thus in L - R circuit, we have

Z = √(R² + X²L)

Where R and XL are resistance and inductive reactance.

But XL = ⍵L.

Z = √(R² +(⍵L)²)

As a resistance, impedance also has a unit, and what is the unit of impedance. The answer is the SI unit of impedance is ‘ohm’.

But a term derived from impedance is admittance. So, what is the admittance? We can define admittance as, “The reciprocal of impedance is called ‘admittance’.” Unit of impedance is ‘mho’ or ‘ohm-¹’ (Ω-¹) or ‘siemen’ (S). Admittance formula is

Y = 1/Z

Impedance and admittance both are reciprocal to each other.

Related Topics,

The impedance of R - C series circuit;-

i = V/√(R² + X²C)

Similarly, Z = √(R² + X²c)

Where R and Xc are resistance and capacitive reactance.

But Xc = 1/⍵C.

∴ Z = √(R² + (1/⍵C)²)

Impedance formula of R-L-C series circuit:-

i = V/√ (R² + (X_L- X_c)²)

Similarly, Z = √ (R² + (X_L - X_c)²)

But XL = ⍵L and Xc = 1/⍵C

∴ Z = √ (R² + ( ⍵L- 1/⍵C )²)

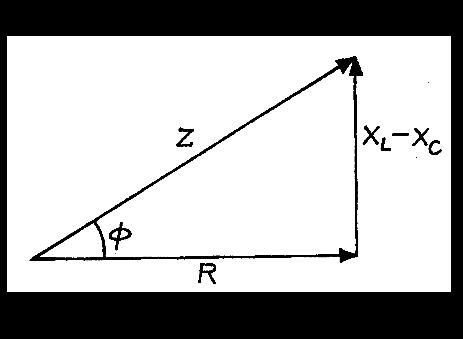
Impedance triangle:- What is impedance triangle? The impedance of an L-C-R circuit is given as

Z = √ (R² + (XL - Xc)²)

And the phase relationship is given by

tan? = XL - Xc/R

In terms of the resistance and the reactances of the circuit, elements may be expressed by means of a right-angled triangle, as shown in fig. This triangle is called an impedance triangle.

right-angled triangle

The impedance of capacitor:- It impedes the flow of current in the capacitor.

The capacitor impedance formula is

Impedance of inductor:- It impedes the flow of current in the inductor. It measures the resistance of the current in the inductor.

Inductor impedance formula is

ZC = jL⍵

Reactance:- What is reactance? We can define reactance as, “The reactance is the opposition offered by an inductor or by a capacitor or by both.” So it is the reactance definition.

Reactance meaning in hindi विरोध. The unit of reactance is ‘ohm’. The reactance symbol is ‘X’

Reactance formula:- The formula of reactance is

X = XL + Xc

Where XL and XC are inductive reactance and capacitive reactance respectively.

Later, we also discuss the XL and Xc formula.

NCERT Physics Notes:

Inductive resistance:-The peak value of current in the coil is

i0 = V0/⍵L

Applying Ohm's law, we find that the product ωL has the dimension of resistance. It represents the effective opposition of the coil to the flow of alternating current. It is known as ‘inductive resistance’. It is denoted by XL.

XL = ωL = 2πfL

Where f is the frequency of the alternating current. Thus, the inductive reactance increases with increasing frequency of the current (XL ∝ f). The graph between XL and f is, therefore, a straight line.

Where L is in henry and f in hertz (cycle/second), then the XL (= 2πfL) inductive reactance unit (or SI unit of reactance )is ohm. The inductive reactance XL is zero for d.c. for which f = 0.

Capacitive reactance:- The peak value of current in the capacitor circuit is

i0 = V0/1/⍵C.

Applying Ohm’s law, we find that the quantity 1/ωC has the dimensions of resistance. It is the effective opposition of the capacitor to the flow of alternating currents. It is known as the reactance of the capacitor or capacitive inductance and is denoted by XC. So, Xc meaning is capacitive reactance.

Xc = 1/ωC = 1/2πfC

Where f is the frequency of the alternating current. Thus, the capacitive reactance decreases with the increasing frequency of current (Xc ∝ 1/f). The graph between the Xc and f, is, therefore, a rectangular hyperbola.

When C is farad and f is in hertz then Xc is in ohm. The capacitive reactance is infinite for d.c. for which f = 0.

The reciprocal of reactance is called ‘susceptance’ of the a.c. circuit. Unit of susceptance is ‘mho’ or ‘ohm-¹’ (Ω-¹) or ‘siemen’ (S). Susceptance meaning in hindi ग्रहणशीलता

Power

Also read :

Reluctance:- Reluctance is like resistance in a magnetic field, it opposes the magnetic flux in the field. The reluctance symbol is S

S = l/μ0μrA

In above we discuss reactance and impedance, and we clearly understand what is reactance and impedance?

Power factor of an alternating-current circuit:- When an alternating current circuit contains, besides resistance, inductance or capacitance or both, then the average power dissipation in the circuit is Vrms ☓ irms ☓ cosϕ when is phase difference between voltage and current. The factor is called power factor where cosϕ

There is a 5 Ω resistance in an AC circuit. Inductance of 0.1 H is connected with it in series. If equation of AC e.m.f is 5 sin 50t then the phase difference between current and e.m.f is:

Solution:- R = 5Ω,

L = 0.1 H

ω = 50

We know that, cosφ = R/Z = R/√(R² +(⍵L)²) = 5/√{(5)² + (50 ✖ 0.1)²}

Cosφ = 5/ √{25 + 25} = 5/√50 = 5/5√2 = 1/√2

Cosφ = cos 45°

Φ = ?/4

Power factor of the following circuit will be zero

Inductor
Capacitor
Conductor and inductor
Resistor

Ans: Option (iii) is correct

Also check-

Frequently Asked Questions (FAQs)

Q: What is the significance of impedance in the design of microwave circuits?

In microwave circuits, impedance control is critical for signal integrity, power transfer, and minimizing reflections. Techniques like impedance matching, quarter-wave transformers, and stub tuning are used to optimize circuit performance at high frequencies. Proper impedance design is essential for efficient microwave systems.

Q: How does impedance affect the operation of plasma devices?

In plasma devices, impedance plays a crucial role in coupling energy from power sources to the plasma. It affects plasma ignition, stability, and energy transfer efficiency. Understanding plasma impedance is essential for designing efficient plasma processing equipment and fusion reactors.

Q: What is the concept of acoustic impedance in musical instrument design?

Acoustic impedance in musical instruments affects tone production and quality. It represents the resistance to air flow and vibration in the instrument's body. Understanding and manipulating acoustic impedance is crucial for designing instruments with desired tonal characteristics and playing responsiveness.

Q: How does impedance affect the performance of phased array antennas?

In phased array antennas, controlling the impedance of individual elements and their mutual coupling is crucial for beam forming and steering. Impedance variations can affect the array's radiation pattern, sidelobe levels, and overall efficiency. Proper impedance management is essential for high-performance phased arrays.

Q: What is the role of impedance in superconducting circuits?

In superconducting circuits, the concept of kinetic inductance leads to a unique form of impedance. Understanding and controlling this impedance is crucial for designing superconducting qubits, SQUID magnetometers, and other quantum devices that exploit the properties of superconductors.

Q: How does the concept of impedance apply to quantum circuits?

In quantum circuits, impedance relates to the quantum of resistance (h/e²) and affects the behavior of quantum devices like superconducting qubits. Understanding and controlling impedance at the quantum level is crucial for quantum information processing and superconducting electronics.

Q: What is the concept of wave impedance in optical fibers?

In optical fibers, wave impedance relates to the ratio of electric to magnetic field strengths of the propagating light. It affects mode propagation, dispersion, and coupling efficiency. Understanding wave impedance is crucial for designing efficient fiber optic systems and interfaces.

Q: How does impedance affect the behavior of filters in AC circuits?

Impedance plays a crucial role in filter design and performance. The frequency-dependent nature of reactive impedances allows for the creation of low-pass, high-pass, band-pass, and band-stop filters. The impedance characteristics determine the filter's cutoff frequency, roll-off rate, and overall response.

Q: What is the significance of complex impedance in bioelectrical measurements?

In bioelectrical measurements, complex impedance provides information about biological tissues' electrical properties. The resistive component relates to extracellular fluid, while the reactive component indicates cell membrane capacitance. This helps in tissue characterization and medical diagnostics.

Q: How does impedance affect the resonant frequency of an LC circuit?

The resonant frequency of an LC circuit occurs when inductive and capacitive reactances are equal in magnitude but opposite in sign, resulting in minimum impedance. The formula for resonant frequency, f = 1 / (2π√LC), is derived from this impedance relationship.

Articles

DU LLB Fee Structure 2026 - Check Complete Details

Sep 11, 2025

Top 5 Career Options after B.Arch - Eligibility, Salary Trends

Sep 11, 2025

Top 6 Career Options after BAF - Eligibility, Salary

Sep 06, 2025

Gujarat Paramedical Merit List 2025 Revised (Out): Download PDF Rank List

Sep 04, 2025