Stress and Strain - Definition, Curve, Hooke's Law, SI Units, Types, FAQs

What is Stress?

The restoring force or deforming force experienced per unit area on a body is called stress. It has the dimension of force per area or the same dimension as that of pressure.

Stress $=\frac{\text { Force }}{\text { Area }}$

$
1 \mathrm{~N} / \mathrm{m}^2=1 \mathrm{~Pa}(\text { pascal })
$
The SI unit of stress is pascal ( Pa ).

Types of Stress

When a force is applied on a body and it causes deformation (change in shape or size), the internal restoring force per unit area developed inside the body is called stress.

There are mainly three types of stress:

1. Longitudinal Stress (Normal Stress):Produced when the force is applied along the length of an object.
   It can be of two types:

• Tensile Stress: When the object is stretched (length increases).
• Compressive Stress: When the object is compressed (length decreases).
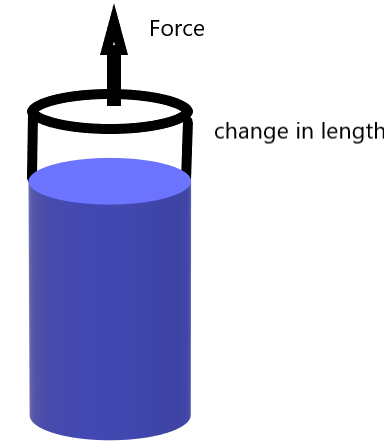
  A. Tensile Stress
  The stress developed inside the body is called tensile stress when the length of the body increases In the direction of the applied force.
  Here in the below image, you can see that when the force is applied in a particular direction the length of the body increases in the same direction as that of the applied force.
  
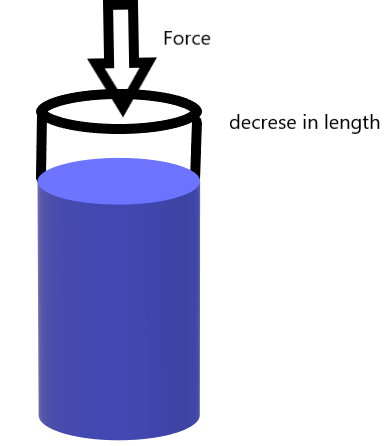
  B. Compressive Stress
  The stress developed inside the body is called compressive stress when the length of the body decreases in the direction of the force applied.
  
  Here in the figure below you can see that the length of the body decreases in the direction of the applied force.
  

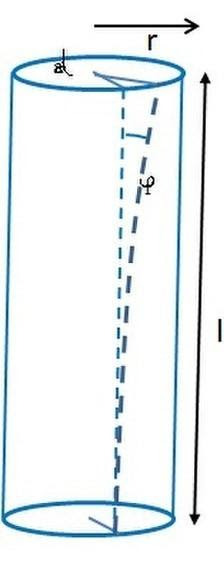
2. Tangential or Shearing Stress
   Tangential stress occurs when an elastic restoring force or deforming force operates parallel to the surface area. Here in the figure below you can see that the force is applied along a surface and it is called tangential because the force is not perpendicularly applied rather it is applied tangentially to the surface.
   

What is Strain?

When a body is deformed due to an applied force, strain measures how much the body changes in shape or size compared to its original dimensions.

Definition:

$
\text { Strain }=\frac{\text { Change in dimension }}{\text { Original dimension }}
$

Types of Strain:

1. Tensile Strain: When a body stretches,

$
\text { Tensile Strain }=\frac{\text { Increase in length }}{\text { Original length }}
$

2. Compressive Strain: When a body compresses,

$
\text { Compressive Strain }=\frac{\text { Decrease in length }}{\text { Original length }}
$

3. Shear Strain: When a body changes shape due to forces applied parallel to its surface.

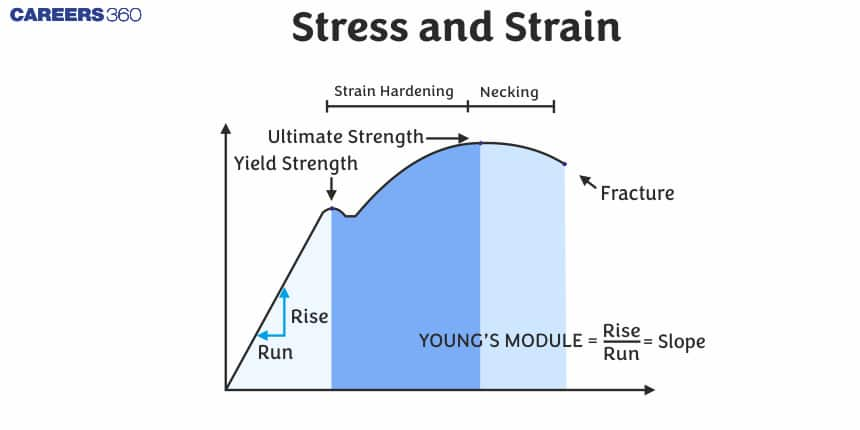
Stress-Strain Curve

A line created by stress and strain is known as the stress-strain curve. A stress-strain curve for a material gives the relationship between stress and strain in the ideal case of Hooke's law. It's calculated by progressively adding load to a test coupon and measuring deformation, from which stress and strain may be calculated (see tensile testing). Many properties of a material are revealed by these curves, including Young's modulus, yield strength, and ultimate tensile strength.

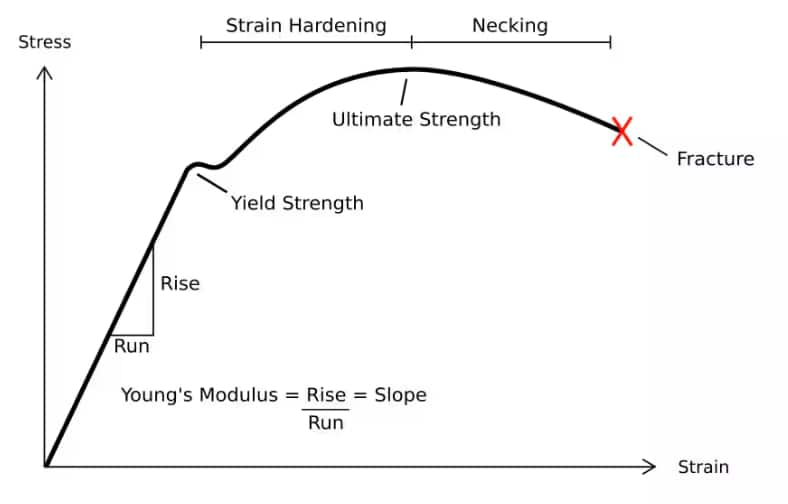
What is Hooke's Law ?

Hooke's Law states that within the elastic limit of a material, the stress applied to it is directly proportional to the resulting strain.

$
\sigma=Y \varepsilon
$
Where:
$\sigma=$ stress (force per unit area, in Pa)
$\varepsilon=$ strain (relative deformation, dimensionless)
$Y=$ Young's modulus of the material (a measure of stiffness)

What is Modulus of Elasticity?

The modulus of elasticity of a material is a measure of how resistant it is to deformation under stress. In simple words, it tells us how "stiff" a material is. It is the ratio of stress to strain within the elastic limit of the material.

$
\text { Modulus of Elasticity }=\frac{\text { Stress }}{\text { Strain }}
$

Stress $(\sigma)=$ force per unit area
Strain $(\varepsilon)=$ fractional change in shape or size

Types of Modulus of Elasticity

1. Young's Modulus (Y)

• Measures resistance to linear (tensile or compressive) deformation.
• Formula: $Y=\frac{\text { Tensile or Compressive Stress }}{\text { Linear Strain }}$
• Unit: Pascal (Pa)

2. Bulk Modulus (K)

• Measures resistance to uniform volume change (compression).
• Formula: $K=\frac{\text { Hydrostatic Pressure }}{\text { Volumetric Strain }}$
• Unit: Pascal (Pa)
• Used for liquids and solids under pressure.

3. Shear Modulus (G) or Modulus of Rigidity

• Measures resistance to shape change without volume change (shear deformation).
• Formula: $G=\frac{\text { Shear Stress }}{\text { Shear Strain }}$
• Unit: Pascal (Pa)
• Used for deformation like twisting or sliding layers.

What are the limitations of Hooke's Law?

• Valid only up to the elastic limit.
• Does not apply to plastic or permanent deformation.
• Assumes uniform, perfect material.
• Ignores time-dependent effects like creep.
• Fails at very large stresses or strains.

Recommended Topic Video