Uniform Circular Motion - Definition, Examples, Diagram, Characteristic, Examples, FAQs
An object is said to be in a uniform circular motion when it travels a circular path at constant speed. This means that equal distances along the circular path are traveled in equal intervals of time; however, the direction of motion is continuously changing. In this article, we shall study the complex mechanism of uniform circular motion: what forces allow for circular motion and how velocity and acceleration apply in this context.
This Story also Contains
- What Is Uniform Circular Motion?
- Uniform Circular Motion Formula
- Terms Related to Uniform Circular Motion
- Relation Between Angular Acceleration and Tangential Acceleration
- Uniform Circular Motion Questions and Answers
This concept fits into the greater picture of kinematics, which is very important in Class 11 physics. Thus, it is important for board exams and competitive examinations conducted by different national authorities such as the Joint Entrance Examinations (JEE Main) and the National Eligibility Entrance Test (NEET), apart from others like SRMJEE, BITSAT, WBJEE, and BCECE. The concept has been asked nine times over the past ten years in the JEE Main examination. For NEET, five questions were asked about this concept.
What Is Uniform Circular Motion?
Circular motion is the motion of a body travelling in a path around a fixed point in the shape of a circle. Uniform circular motion implies that if the body travels equal distances along the circumference of the circle in equal intervals of time, then the motion is said to be uniform circular motion. Naturally, this means that it is a type of circular motion in which the speed is maintained while the direction of the velocity is altered.
Uniform circular motion examples:
(i) Motion of the moon around the Earth
(ii) Motion of a satellite around its planet
Note: Circular motion is also known as accelerated motion
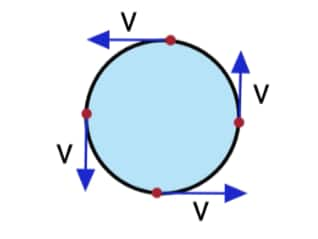
Uniform Circular Motion Formula
Uniform circular motion Formula Class 9 or other classes are given here.
In uniform circular motion, a particle moves with constant speed.
- Angular displacement $\Delta \theta=\frac{\operatorname{Arc}\left(P P^{\prime}\right)}{r}$
- Angular velocity $\omega=\frac{\Delta \theta}{\Delta t}=\frac{2 \pi}{T}=2 \pi v$
- Linear speed $v=r_\omega$
Centripetal acceleration is due to a change in direction of velocity and is always directed towards the centre.
$
a={v^2/r}=r \omega^2=4 \pi^2 v^2 r=v \omega
$
Terms Related to Uniform Circular Motion
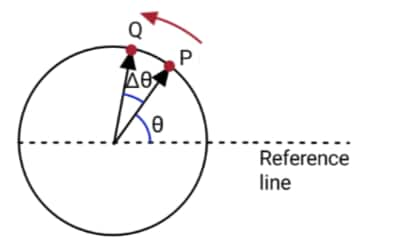
The term related to circular motion is given below:
Radius vector
The vector joining the centre of the circular path to the position on the circular path is called the radius vector.
Angular position
The angle made by the radius vector with a reference line (arbitrarily chosen diameter) is called angular position. The direction of angular position can be clockwise or anticlockwise depending upon the choice of frame of reference. The angular position of the particle at position "P" is denoted by the y $\text { angle } \theta$ in the diagram above.
Angular displacement
The change in angular position is called angular displacement. It is the angle through which the radius vector rotates during the given circular motion.
The angular displacement between positions 'P' and 'Q' is denoted $\text { by } \Delta \theta$ in the diagram above with the S.I unit of angular position and angular displacement is Radian.
Angular velocity
Denoted by $\omega$ (omega)
$\omega$-Rate of change of angular displacement.
Average angular velocity-
$
\omega_{\text {avg }}=\frac{\Delta \theta}{\Delta t}
$
Instantaneous angular velocity
$
\omega=\frac{d \theta}{d t}
$
S.I. units- Radian per second (rad per sec )
$\omega$ is a vector quantity
The direction of $\omega$ is given by the Right-hand rule.
According to the right-hand rule, if you hold the axis with your right hand and rotate the fingers in the direction of motion of the rotating body, then the thumb will point in the direction of the angular velocity.
Angular Acceleration
The rate of change of angular velocity with time is said to be Angular Acceleration.
$
\alpha=\frac{\Delta \omega}{\Delta t}
$
- SI units- $\operatorname{rad} .(\mathrm{sec})^{-2}$
- Angular Acceleration is a vector quantity.
The direction of Angular Acceleration
a) If angular velocity is increasing then the direction of Angular Acceleration is in the direction of angular velocity.
b) If angular velocity is decreasing then the direction of Angular Acceleration is in the direction which is opposite to the direction of angular velocity.
Time is taken to complete one rotation
Formula-
$
T=\frac{2 \pi}{\omega}
$
Where $\omega=$ angular velocity
If $\mathrm{N}=\mathrm{no}$. of revolutions and total time then
$
T=\frac{t}{N} \text { or } \quad\left(\omega=\frac{2 \pi N}{t}\right)
$
- S.I unit - seconds (s)
Frequency
The total number of rotations in one second.
Formula-
$
\nu=\frac{1}{T}
$
- S.I. unit $=$ Hertz
We can write the relation between angular frequency and frequency as
$
w=2 \pi \nu
$
Centripetal Acceleration and Tangential acceleration
Centripetal acceleration: When a body is moving in a uniform circular motion, a force is responsible for changing the direction of its velocity. This force acts towards the centre of the circle and is called centripetal forceThe acceleration produced by this force is centripetal acceleration.
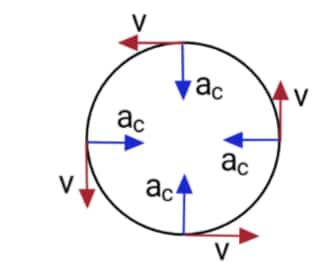
Formula-
$
a_c=\frac{V^2}{r}
$
Where $a_c=$ Centripetal acceleration,
$\mathrm{V}=$ linear velocity
$r=$ radius
Tangential acceleration: During circular motion, if the speed is not constant, then along with centripetal acceleration, there is also a tangential acceleration, which is equal to the rate of change of magnitude of linear velocity.
$a_t=\frac{\mathrm{d} v}{\mathrm{~d} t}$
Relation Between Angular Acceleration and Tangential Acceleration
$\overrightarrow{a_t}=\vec{\alpha} \times \vec{r}$
Where:
- $\overrightarrow{a_t}=$ Tangential acceleration (linear acceleration along the tangent to the circular path)
- $\vec{\alpha}=$ Angular acceleration vector (rate of change of angular velocity)
- $\vec{r}^*=$ Position vector (radius vector from axis of rotation to the point of interest)
Total acceleration
The vector sum of Centripetal acceleration and tangential acceleration is called Total acceleration.
Formula-
$a_n=\sqrt{a_c^2+a_t^2}$
The angle between Net acceleration and tangential acceleration $(\theta)$
From the above diagram-
$
\tan \theta=\frac{a_c}{a_t}
$
Also Check-
Uniform Circular Motion Questions and Answers
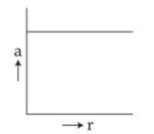
Example 1: If a body moving in a circular path maintains a constant speed of 10 ms-1, then which of the following correctly describes the relation between acceleration and radius?
1) 
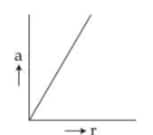
2) 
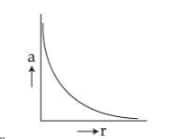
3) 
4) 
Solution:
$a=\frac{v^2}{r}$
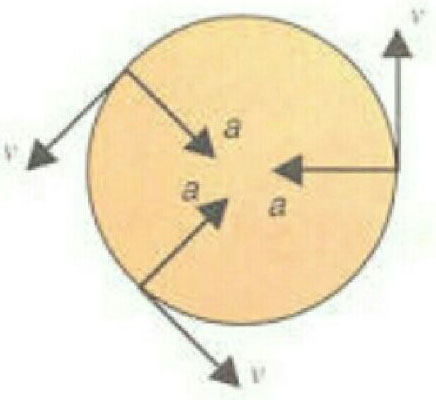
Figure Shows Centripetal acceleration
$\begin{aligned}
& a=\frac{v^2}{r} \because|\vec{v}|=\text { constant } \\
& a \propto \frac{1}{r} \text { or } a r=\text { constant }
\end{aligned}$
Hence, the graph between a and r will be a hyperbola.
Example 2: A Point P moves in a counter-clockwise direction on a circular path as shown in the figure. The movement of $P$ is such that it sweeps out a length that is in metres and $t$ is in seconds. The radius of the path is $\mathbf{2 0 ~ m}$, The acceleration (in $\mathrm{m} / \mathrm{s}^2$ ) of $P$ When $t=2 s$ is nearly
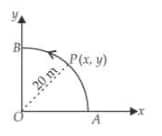
1) 14
2) 13
3) 12
4) 7.2
Solution:
$
\begin{aligned}
& \text { As } S=t^3+3 \\
& V=\frac{d s}{d t}=3 t^2+0 \\
& \Rightarrow v=3 t^2
\end{aligned}
$
tangential acceleration
$
\begin{aligned}
& =a_t=\frac{d v}{d t}=\frac{d\left(3 t^2\right)}{d t} \\
& a_t=6 t
\end{aligned}
$
At $t=2 \mathrm{sec}$
$
\begin{aligned}
& v=3(2)^2=12 \mathrm{~ms}^{-1} \\
& a_t=6 \times 2=12 \mathrm{~ms}^{-2}
\end{aligned}
$
$
\begin{aligned}
& \therefore \text { centripetal acceleration }=\vec{a}_c=\frac{v^2}{r}=\frac{(12)^2}{20}=\frac{144}{20} \\
& a_c=7.2 \mathrm{~ms}^{-2}
\end{aligned}
$
$\therefore$ Net acceleration
$
\begin{aligned}
& a=\sqrt{a_c^2+a_t^2}=\sqrt{7.2^2+12^2} \\
& a_c \simeq 14 \mathrm{~ms}^{-2}
\end{aligned}
$
Example 3: A particle is moving with speed varying as v = 2t, then the angle which the resultant acceleration makes with the radial direction (R=1m) at t = 2 is
$\begin{aligned} & \text { 1) } \tan ^{-1}\left(\frac{1}{2}\right) \\ & \text { 2) } \tan ^{-1}\left(\frac{1}{6}\right) \\ & \text { 3) } \tan ^{-1}\left(\frac{1}{8}\right) \\ & \text { 4) } \tan ^{-1}\left(\frac{1}{4}\right)\end{aligned}$
Solution:
The angle between Total acceleration and centripetal acceleration is given by
$
\tan \phi=\frac{a_t}{a_c}=\frac{r^2 \alpha}{V^2}
$
where
$\alpha=$ angular acceleration
$V=$ velocity
$r=$ radius of circle
So From the below figure
$\begin{aligned}
& \tan \theta=\frac{a_t}{a_r} \\
& a_t=\frac{\mathrm{d} v}{\mathrm{~d} t}=2 \mathrm{~m} / \mathrm{s}^2 \\
& a_r=\frac{v^2}{R} \\
& a_r=\frac{4 t^2}{1}=4 \times 2^2=16 \\
& \therefore \tan \theta=\frac{2}{16}=\frac{1}{8} \\
& \therefore \theta=\tan ^{-1}\left(\frac{1}{8}\right)
\end{aligned}$
Example 4: A particle is moving with a constant speed of 8 m/s in a circular path of radius 1 m. What will be the displacement of the particle in 1 sec?
1) 2 sin 80
2) 2 sin 40
3) 4 sin 80
4) 4 sin 40
Solution:
Displacement in Circular Motion -
$
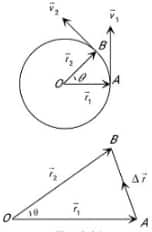
\Delta r=2 r \sin \frac{\theta}{2}
$
$\Delta r=$ displacement
$\theta=$ Angle between two vectors
- wherein
$
\text { If }\left|\overrightarrow{r_1}\right|=\left|\overrightarrow{r_2}\right|=r
$
Let the angular displacement of the particle from $\mathrm{A}$ to $\mathrm{B}$ will be
$
2 R \sin \frac{\Theta}{2}
$
Length of circular arc $A B=8 * 1=8 \mathrm{~m}$
$
\begin{aligned}
& \text { Angle } \Theta=\frac{\text { arc length }}{\text { Radius }}=\frac{\Theta}{1}=8 \mathrm{rad} \\
& d=2 R \sin \frac{\Theta}{2}=2 * 1 * \sin \frac{8}{2} \\
& 2 \sin 4^0
\end{aligned}
$
Hence, the correct answer is option (2).
Uniform circular motion involves a particle moving with constant speed along a circular path, whose velocity continuously changes due to the continuous change in direction. A simple example is the merry-go-round in which objects move in circles at an even speed. This concept also applies to natural phenomena like planets orbiting the sun. This understanding of uniform circular motion allows us to comprehend how forces and motion work in circular paths, which is essential for our daily lives and for grasping bigger movements in cosmology.
Related Study Resource,
Frequently Asked Questions (FAQs)
Centripetal force (F) and centripetal acceleration (a) are directly related through Newton's Second Law of Motion: F = ma, where m is the mass of the object. The centripetal force causes the centripetal acceleration, which is always directed towards the center of the circular path.
While the actual motion of electrons in atoms is more complex and governed by quantum mechanics, the Bohr model of the atom uses the concept of uniform circular motion as a simplified representation. In this model, electrons are thought to orbit the nucleus in circular paths, with the electrostatic force acting as the centripetal force. This simplified model helps in understanding basic atomic structure and energy levels.
Angular displacement is the angle through which an object rotates in circular motion, measured in radians or degrees. Linear displacement is the straight-line distance between the initial and final positions of the object. In uniform circular motion, the angular displacement increases continuously, while the linear displacement oscillates and can never exceed the diameter of the circle.
In uniform circular motion, the tangential acceleration is zero because the speed of the object remains constant. All the acceleration is in the radial direction (towards the center), which is the centripetal acceleration. This constant speed but changing direction is what defines uniform circular motion and distinguishes it from other types of circular motion where speed may vary.
The centripetal force is crucial in maintaining uniform circular motion as it constantly pulls the object towards the center of the circle, changing its direction but not its speed. If the centripetal force is suddenly removed, the object will continue moving in a straight line tangent to the circle at the point where the force was removed, following Newton's First Law of Motion.
The ratio v²/r in uniform circular motion represents the centripetal acceleration. This ratio remains constant for a given circular motion, regardless of the mass of the object. It shows that for a fixed radius, the acceleration increases with the square of the velocity, and for a fixed velocity, the acceleration is inversely proportional to the radius. This relationship is crucial in designing safe curves on roads and in understanding planetary orbits.
When a charged particle enters a uniform magnetic field perpendicular to its velocity, it experiences a magnetic force perpendicular to both its velocity and the magnetic field. This force acts as the centripetal force, causing the particle to move in a circular path. The radius of this path depends on the particle's mass, charge, velocity, and the strength of the magnetic field. This principle is used in devices like mass spectrometers and cyclotrons.
The spin cycle in a washing machine utilizes uniform circular motion to remove water from clothes. As the drum rotates at high speed, the clothes are pressed against the drum's perforated walls. The centripetal force keeps the clothes in circular motion, while water, being denser, experiences a greater outward force and is forced through the perforations. This application demonstrates how the principles of circular motion can be used for practical purposes in everyday appliances.
The centripetal force being perpendicular to the velocity in uniform circular motion is crucial because it ensures that the force only changes the direction of motion, not the speed. This perpendicular relationship means that the force does no work on the object, as work is only done when a force has a component parallel to the displacement. Consequently, the kinetic energy of the object remains constant, maintaining the uniform speed characteristic of this type of motion.
Roundabouts in traffic systems are designed based on principles of uniform circular motion. The circular design allows vehicles to maintain a relatively constant speed while changing direction, which is more efficient than coming to a complete stop at an intersection. The radius of the roundabout is calculated to allow for safe navigation at appropriate speeds, considering factors like centripetal force, friction, and typical vehicle capabilities. This application of circular motion principles helps in creating smoother, safer traffic flow.