Electronic Configuration Of Elements

Electronic Configuration of Elements-

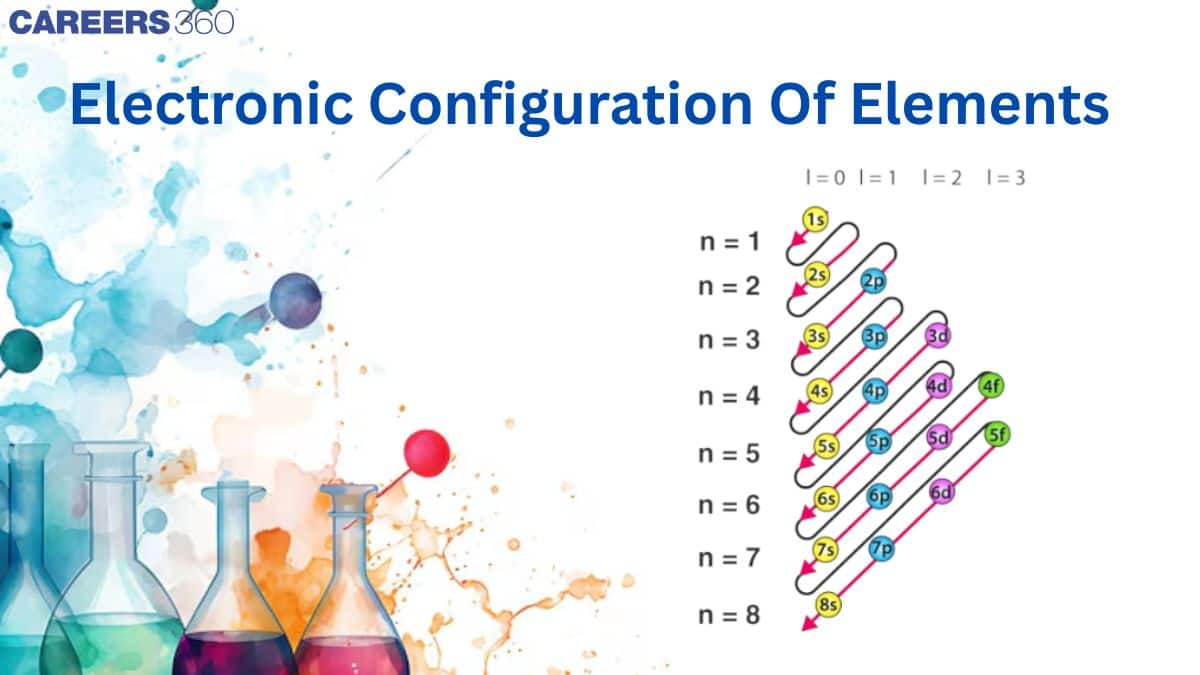
Writing of electronic configuration of any element is based on three rules as told in previous concepts. They are:

1. Aufbau principle

2. Pauli’s exclusion principle

3. Hund’s rule of maximum multiplicity

The distribution of electrons into different shells, subshells and orbitals of an atom is called its electronic configuration. Keeping in view the above rules, and representing an orbital by a box and an electron with its direction of spin by a arrow, the electronic configuration of the atom of any element can be represented.

Alternatively, the electronic configuartion of any orbital can be simply represented by the notation, $\mathrm{nl}^{\mathrm{x}}$.

Where, n = number of the main or principal shell, l = symbol of the subshell or orbital (s, p, d, f), x = number of electrons present in that orbital.

Thus, 4p¹ means that the p-subshell of the 4th main shell contains one electron.

The electronic configuration of the different elements can be represented in two ways:

1. Subshell notation

2. Orbital diagram

Let’s understand with the help of examples:

1. The hydrogen atom has only one electron which goes into the orbital with the lowest energy, namely 1s. The E.C of hydrogen is 1s¹ (subshell notation)

Orbital diagram:

2. The electronic configuration of lithium is 1s² 2s¹. Lithium has 3 electrons, as its atomic number is 3. 2 electrons filled in 1s orbital and 1 electron filled in 2s orbital.

let us consider fluorine (Z = 9) :

F(Z = 9) = 1s², 2s², 2px², 2py², 2pz¹ or

The importance of knowing the exact electronic configuration of an element lies in the fact that the chemical properties of an element are dependent on the behaviour and relative arrangement of its electrons.

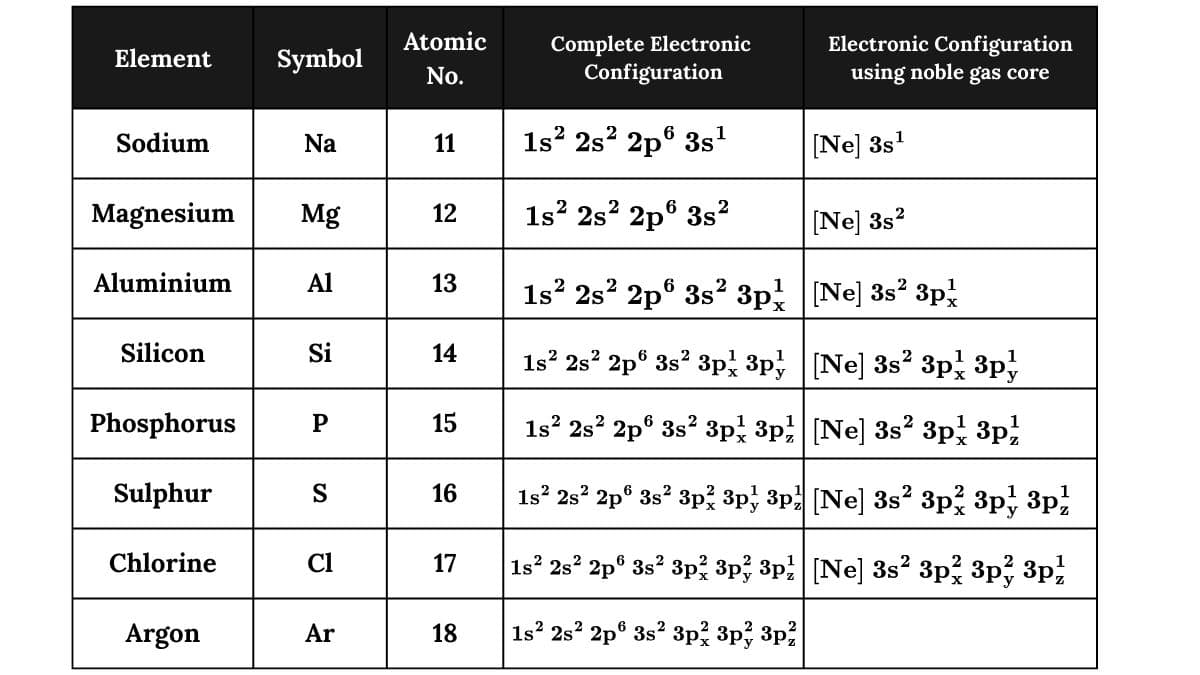
Sodium (Z = 11) to Argon ( Z = 18), the electronic configuration of these elements are written exactly in the manner described above. In these elements, 3s and 3p orbitals are successively filled with electrons one at a time following the general principles discussed earlier.

However, for the sake of simplicity, the detailed electronic configuration of the noble gas core preceding the valence electrons is represented by the symbol of the noble gas in square brackets. This is illustrated in table below:

Potassium (Z = 19) and Calcium (Z = 20). With potassium, the filling of the 4s orbital begins since the energy of the 4s-orbital is slightly lower than those of the 3d orbitals. Thus,

K (Z = 19), 1s² 2s² 2p⁶ 3s² 3p⁶ 4s¹ or [Ar] 4s¹

Ca (Z = 20), 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² or [Ar] 4s²

Here, [Ar] represents the argon noble gas core, i.e., 1s² 2s² 2p⁶ 3s² 3p⁶.

Note: The electron added in going from one element to the next is called differentiating electron. It makes the configuration of the atom different from that of the atom that preceds it. The differentiating electron is added in each step to the orbital of lowest energy available to it.

Recommended topic video on (Electronic Configuration of Elements)

Also Check-

• NCERT Exemplar Class 11th Chemistry Solutions
• NCERT Exemplar Class 12th Chemistry Solutions
• NCERT Exemplar Solutions for All Subjects\

Solved Examples Based On Electronic Configuration of Elements

Example 1: The electronic configuration of copper is:

1)$[\operatorname{Ar}] 3 d^{10} 4 s^1$

2) $[\mathrm{Ar}] 3 d^9 4 s^2$

3) $[\operatorname{Ar}] 3 d^{10} 4 s^2$

4) $[\mathrm{Ar}] 3 d^8 4 s^2$

Solution: Ideally, the electronic configuration of Cu must be $[\mathrm{Ar}] 3 \mathrm{~d}^9 4 \mathrm{~s}^2$ but in this case, the electrons in d-orbitals are not symmetrically filled. Thus to maintain the symmetricity, one electron from the 4s-orbital goes to the d-orbital and thus Cu maintains the electronic configuration as$[\mathrm{Ar}] 3 \mathrm{~d}^{10} 4 \mathrm{~s}^1$.

Hence, the answer is the option (1)

Example 2: Which law indicates the pairing of electrons in the same orbital?

1) Newton’s first law

2) Hund’s rule

3) Aufbau principle

4) Pauli exclusion principle

Solution: Hund’s rule states that “pairing of electrons in the orbitals belonging to the same subshell (p, d or f) does not take place until each orbital belonging to that subshell has got one electron each. It is singly occupied”.

Hence, the answer is the option (2).

Example 3: In which of the following pairs, the outermost electronic configuration will be the same?

1) $\mathrm{Cr}^{+}$and $\mathrm{Mn}^{2+}$
2) $\mathrm{V}^{2+}$ and $\mathrm{Cr}^{+}$
3) $\mathrm{Ni}^{2+}$ and $\mathrm{Cu}^{+}$
4) $\mathrm{Fe}^{2+}$ and $\mathrm{Co}^{+}$

Solution: The outermost electronic configurations-

$\begin{aligned} & \mathrm{Cr}^{+} \rightarrow[\mathrm{Ar}] 3 \mathrm{~d}^5 \mathrm{Mn}^{2+} \rightarrow[\mathrm{Ar}] 3 \mathrm{~d}^5 \\ & \mathrm{~V}^{2+} \rightarrow[\mathrm{Ar}] 3 \mathrm{~d}^3 \mathrm{Cr}^{+} \rightarrow[\mathrm{Ar}] 3 \mathrm{~d}^5 \\ & \mathrm{Ni}^{2+} \rightarrow[\mathrm{Ar}] 3 \mathrm{~d}^8 \mathrm{Cu}^{+} \rightarrow[\mathrm{Ar}] 3 \mathrm{~d}^{10}\end{aligned}$

In Cr⁺and Mn²⁺, the outermost electronic configuration is the same.

Hence, the answer is the option (2).

Example 3: In the sixth period, the orbitals that are filled are :

1) 6s, 4f, 5d, 6p

2) 6s, 5d, 5f, 6p

3) 6s, 5f, 6d, 6p

4) 6s, 6p, 6d, 6f

Solution: Energy order of orbitals according to Aufbau principle-

The order of orbitals filling is 6s, 4f, 5d, 6p.

Therefore, the correct option is (1).

Example 4: Element "E" belongs to the period 4 and group 16 of the periodic table. The valence shell electron configuration of the element, which is just above "E" in the group is

1) 3s²,3p⁴
2) 3d¹⁰,4s²,4p⁴
3) 4d¹⁰,5s²,5p⁴
4) 2s²,2p⁴

Solution:
The element " E " will be Se (Selenium), it belongs to period 4 and group 16 of the periodic table.
Just above Se, S (sulfur) is present. The valence shell electronic configuration of Sulfur is 3s²,3p⁴
Hence, the answer is the option (1).

Example 5: The electronic configuration of Pt (atomic number 78) is :
1)$[\mathrm{Xe}] 4 \mathrm{f}^{14} 5 \mathrm{~d}^9 6 \mathrm{~s}^1$
2) $\left[K_r\right] 4 f^{14} 5 d^{10}$
3) $[X e] 4 f^{14} 5 d^{10}$
4) $[\mathrm{Xe}] 4 f^{14} 5 d^8 6 s^2$

Solution:

The electronic configuration of Pt (78) is [Xe]4f¹⁴5 d⁹6 s¹

Hence, the answer is the option (1).

Example 6: In an atom, total number of electrons having quantum numbers $\mathrm{n}=4,\left|\mathrm{~m}_{\mathrm{l}}\right|=1$ and $\mathrm{m}_{\mathrm{s}}=-\frac{1}{2}$ is_____

[JEE Main 2024]

Solution:

$\mathrm{n}=4$
$\begin{array}{ll}\ell & \mathrm{m}_{\ell} \\ 0 & 0 \\ 1 & -1,0,+1 \\ 2 & -2,-1,0,+1,+2,+3\end{array}$
So number of orbital associated with
$\mathrm{n}=4,\left|\mathrm{~m}_{\ell}\right|=1 \text { are } 6$

Now each orbital contain one $e^{-}$with $m_s=-\frac{1}{2}$

Hence, the answer is (6).

Conclusion

All in all, the study of electronic configurations deepens one’s understanding of how atoms are built and how this shapes the chemical world. On this basis, we eventually explain the reactivity, bonding, as well as behaviours of different elements in the periodic table by understanding the distribution of electrons’ energy levels in the atomic structures. Pauli exclusion principle states that no two electrons present in an atom can have the same four quantum numbers and Hund’s rule for establishing the electron configuration to minimize energy is critical in the chemists’ attempts to predict the chemical properties of an element and its reactivity with other substances.

NCERT Chemistry Notes:

• NCERT Notes Class 11th Chemistry
• NCERT Notes Class 12th Chemistry
• NCERT Notes For All Subjects