Structure of the Atom - Notes, Topics, Formula, Books, FAQs
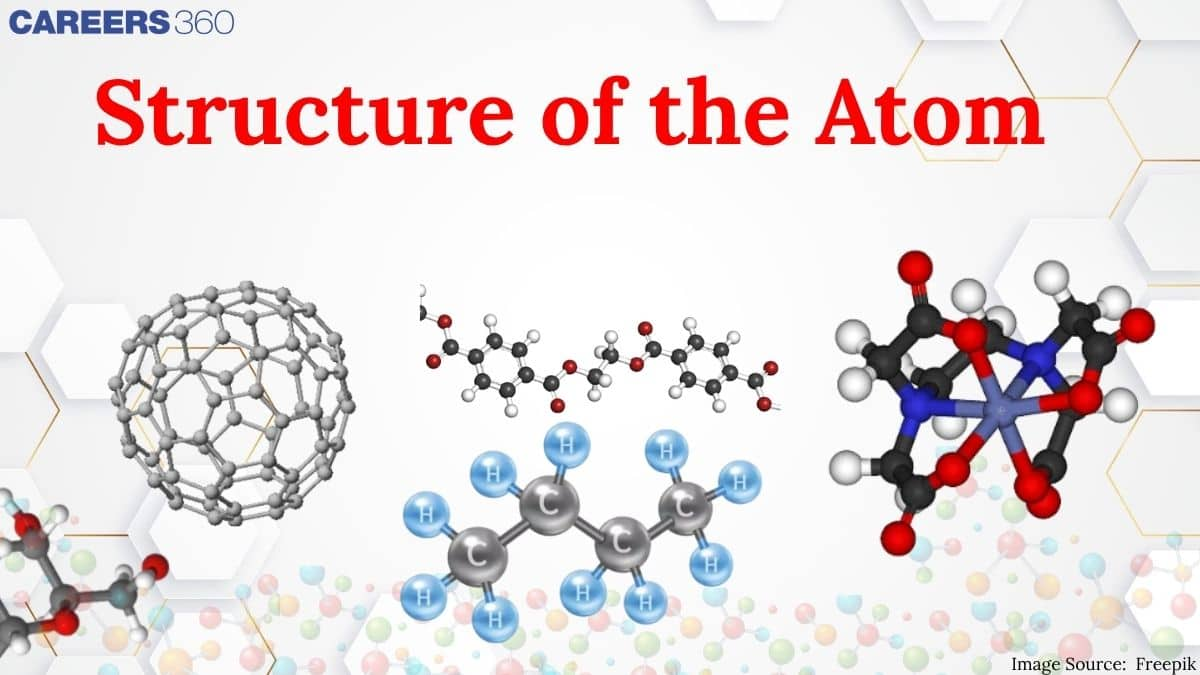
The structure of atom has been studied over the past many decades and has undergone many changes. Atoms are the building block of matter. Over the years, many scientists have come across and given the theories related to it. Dalton was the first to give postulates about the atoms that they were indivisible particles, but subsequent research proved that they have a complicated interior structure. Rutherford's gold foil experiment proposed the presence of a dense nucleus at the centre of the atom, whereas Thomson's model of "plum pudding" explains how electrons were contained in a positively charged sphere where positive and negative charges are disperse in a sphere. Rutherford's concept, however, was not able to explain how electrons do not collapse into the nucleus of the atom because of the opposite charges attraction The important topics of the structure of atoms class 11 are mentioned below in this article.
- Important Topics Of Atomic Structure
- Atomic Structure Overview:
- Line spectrum of hydrogen
- Quantum numbers:
- Atomic structure formula:
- How To Prepare The Atomic Structure
- Essential Reads on Atomic Structure:
- Some Solved Examples
- Conclusion
Atomic structure is a fundamental topic to be studied in chemistry and modern physics. Atoms are extremely important particles that makeup all the materials on Earth. Atoms are present in our bodies and they bond together to form molecules, which make up matter. Everything in the universe is composed of individual atoms of various elements that combine together to form molecules. The basic structure of an atom consists of a nucleus containing protons and neutrons and a cloud of electrons revolving around the nucleus.
In this chapter, the aspirant will learn some important and basic terms electrons, protons, neutrons, atomic number, mass number, isotopes, isobars, velocity, frequency, wavelength, wavenumber, orbitals, quantum numbers, etc.
Important Topics Of Atomic Structure
Thomson Atomic Model:
Thomson had just discovered electrons in 1897, and this was actually the first model to try speaking about the internal configuration of atoms. This is commonly referred to as the "plum pudding model.". Thomson Atomic Model has many postulates which tell about the model.
Rutherford Atomic Model And Its Limitations:
The Rutherford Atomic Model, proposed by Ernest Rutherford, had several limitations like it could not explain the stability of atoms, it did not explain how electrons are arranged inside the atom, and many more.
Electromagnetic Radiation:
Electromagnetic Radiation refers to the transmission of energy through oscillating electric and magnetic fields at the speed of light
Planck's Quantum Theory:
Planck's Quantum Theory states that energy can only be absorbed or emitted by atoms and molecules in discrete quantities which is called Quanta.
Photoelectric Effect:
The Photoelectric Effect is the emission of electrons from a material caused by electromagnetic radiation such as ultraviolet light.
Bohr's Model Of An Atom:
Bohr's Model Of An Atom is a model that describes an atom as a small, positively charged nucleus surrounded by negatively charged electrons in circular orbits.
Hydrogen Spectrum:
The Hydrogen Spectrum is the line spectrum emitted by a hydrogen atom when an excited hydrogen atom returns to its ground state.
De Broglie Relationship:
The De Broglie Relationship describes the relationship between a particle's wavelength and its momentum. It was introduced in 1924 by French physicist Louis de Broglie.
Quantum Numbers:
The Quantum Numbers, are those which describe the location of an electron in an atom. They determine the properties of atomic orbital and electrons in that orbital.
Radial Nodes And Planar Nodes:
Radial Nodes and Planar Nodes are the regions in an orbit where the probability of finding an electron is zero. These are the spherical surfaces around the nucleus.
Frequency, Time Period, And Angular Frequency:
Frequency, Time Period, And Angular Frequency is the important topic of atomic structure. All these are parameters of periodic motion to define it completely. Frequency is defined as the number of vibrations per second or the number of complete oscillations per second. The time period is the time taken by a particular electron to revolve in a particular orbit.
Electronic Configuration:
Electronic Configuration describes the location of an electron around the nucleus of an atom. It is written by following the standard notation.
Stability Of Orbitals: Half-filled And Completely-filled:
Stability Of Orbitals: Half-filled And Completely-filled is the topic of atomic structure in which we study the stability of orbitals as Half-filled and completely-filled orbitals are more stable than other configurations because of symmetry and exchange energy.
Atomic Structure Overview:
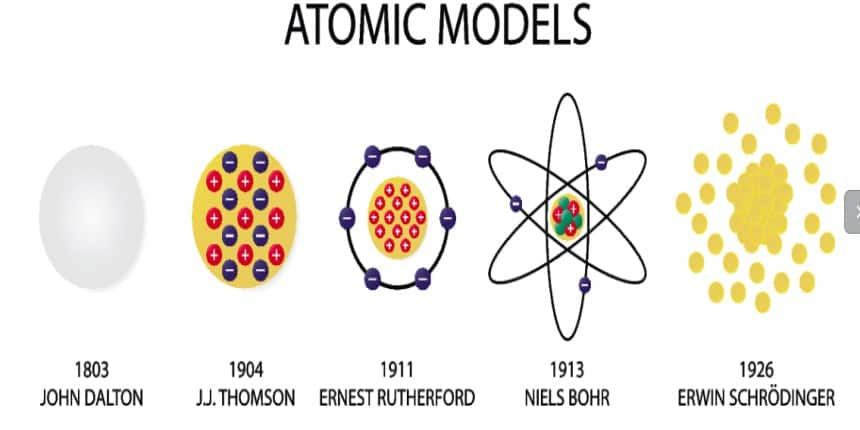
In this chapter, the candidate will, first of all, know about the atomic theory proposed by Dalton in 1808 who regarded the atom as the indivisible particle of matter. At the end of the nineteenth century, it was proved that atoms are divisible and consist of three fundamental particles: Electrons, protons, and neutrons. Faraday then discovered electrons using a cathode ray discharge tube experiment. Neutrons were discovered by James Chadwick by bombarding a thin sheet of beryllium with $\alpha-$ particles. Various atomic models were proposed to explain the structure of the atom. The aspirant will know about Thomson's plum-pudding model, Rutherford's atomic model, and Bohr's model of an atom.
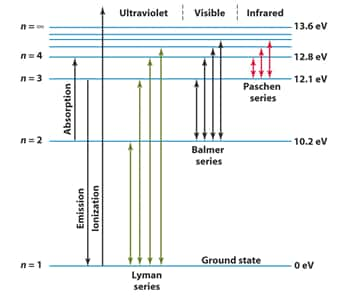
Line spectrum of hydrogen
When an electric discharge is passed through gaseous hydrogen, the $\mathrm{H}_2$ molecules dissociate and the energetically excited hydrogen atoms produced emit electromagnetic radiation of discrete frequencies. These radiations are emitted because of electronic transitions upon de-excitation to different energy levels and on the basis of the final energy level of transition, the hydrogen spectrum consists of several series of lines named after their discoverers like Lyman series, Balmer Series, Paschen Series, Bracket Series, Pfund Series.
Line Spectrum of Hydrogen-like atoms
$
\frac{1}{\lambda}=R Z^2\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)
$
Where $R$ is called Rydberg constant, $R=109677 \mathrm{~cm}^{-1}, Z$ is atomic number
$n_1=$ final orbit occupied after de-excitation $=1,2,3 \ldots$
$\mathrm{n}_2=$ initial orbit occupied before de-excitation
Lyman Series spectrum:
Transition of electrons from higher orbits to $n=1$ result in the Lyman Series
$
n_1=1 \text { and } n_2=2,3,4 \ldots
$
For the H atom, this lies in the Ultraviolet region. For elements with higher $Z$, the Balmer lines lie in the Ultraviolet region
Balmer Series Spectrum:
The transition of electrons from higher orbits to $n=2$ results in the Balmer Series
Where $n_1=2$ and $n_2=3,4,5,6 \ldots$
For H atom, this generally lies in visible region.
Paschen, Bracket and Pfund Series spectrums:
The transition of electrons from higher orbits to $n=3,4$ and 5 respectively result in the Paschen, Bracket and the Pfund Series
These lines lie in the Infrared Region for H atom.
The aspirant will also learn about Planck's quantum theory in which substances absorb or radiate energy discontinuously in the form of small packets. The phenomenon of the photoelectric effect in which there is the ejection of an electron from the surface of a metal when light of suitable frequency strikes on its surface is something very interesting to know in this chapter. Following it an aspirant will come across four quantum numbers like the principal quantum number, azimuthal quantum number, magnetic quantum number and spin quantum number including the shape and size of different orbitals.
The shape of s orbital: (spherical)
.png)
The shape of p orbital:(dumbbell-shaped)
.png)
The shape of the d orbital:
.png)
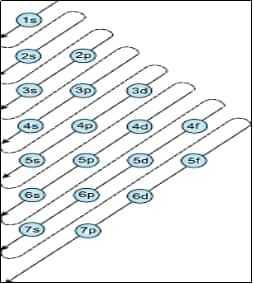
Rules for filling of electrons in various orbitals is a very important part to be studied in this chapter which will be helpful in the rest of the chemistry portion especially in inorganic and organic chemistry.
Rules For Filling Orbitals:
Rule 1 - Aufbau's principle - Lowest energy orbitals are filled first. Thus, the order of filling $1 \mathrm{~s}, 2 \mathrm{~s}, 2 \mathrm{p}, 3 \mathrm{~s}, 3 \mathrm{p}, 4 \mathrm{~s}, 3 \mathrm{~d}$, etc.
Rule 2 - Pauli Exclusion Principle - Only two electrons are permitted per orbital and they must be of opposite spin.
Rule 3- Hund's Rule - No pairing of electron starts in any of the degenerate orbitals until all orbitals of the subshell contain one electron each with parallel spin.
Quantum numbers:
They are the set of four numbers that explain the state of electron i.e., location, energy, type of orbital, orientation of orbital, etc. in an atom. Various quantum numbers are as follows:
1. Principal quantum number( $n$)
2. Azimuthal quantum number($l$)
3. Magnetic quantum number( $m$ )
4. Spin quantum number($s$)
Atomic structure formula:
1. The velocity of the electron in nth Bohr orbit:
$v=2.18 \times 10^8 \frac{Z}{n} \mathrm{~cm} / \mathrm{sec}$
2. The radius of nth Bohr orbital:
$r_n=0.529 \frac{n^2}{z} A^0$
3. The total energy of an electron in nth orbit:
$E_n=-13.6 \frac{z^2}{n^2} \mathrm{eV}$
4. The kinetic energy of electron: -(total energy of electron):
$13.6 \frac{Z^2}{n^2} \mathrm{eV}=-\mathrm{P} \cdot \mathrm{E} / 2$
5.The potential energy of the electron:
$-27.2 \frac{Z^2}{n^2} \mathrm{eV}$
6. Line Spectrum of Hydrogen-like atoms
$
\frac{1}{\lambda}=R Z^2\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)
$
Where R is called Rydberg constant, $R=1.097 * 10^7$ where $\mathrm{Z}=$ atomic number.
7. De-Broglie wavelength
$\lambda=\frac{h}{m v}=\frac{h}{p}$
How To Prepare The Atomic Structure
The first and foremost thing a candidate should do is read the NCERT book thoroughly, with all the topics in this chapter. In order to get away with the confusion of "How to prepare for atomic structure," the aspirant can also take the help of animation and videos which are easily available on the internet, to understand the shape of orbitals, Photoelectric Effect, Bohr's Model Of An Atom, and other related topics. It is very important to have a clear picture of the experimental setup and observations in the mind of the candidate. The candidate should also focus on the previous year's question papers related to atomic structure. Based on the analysis, it is found that most of the numerical problems are from Bohr's theory and the hydrogen spectrum. These are important topics from exam point of view. So, the candidate should try to solve as many problems from these two topics.
Essential Reads on Atomic Structure:
To prepare for atomic structure, these are some reference books that should be consulted;
1. J.D. Lee
2. O.P.Tandon
Also read
| Derivation of Ideal Gas Equation | Nmr Spectroscopy |
| Principle of UV Visible Spectroscopy | Daltons Atomic Theory |
| Difference Between Atom and Molecule |
Some Solved Examples
Example 1: When an electron jumps from $n=4$ to $n=2$ then the change in angular momentum is approximately.
1) $1.1 \times 10^{-34} \mathrm{Js}$
2) (correct) $2.2 \times 10^{-34} \mathrm{Js}$
3) $3.3 \times 10^{-34} \mathrm{Js}$
4) $4.1 \times 10^{-34} \mathrm{Js}$
Solution
The angular momentum of the electron in any $\mathrm{n}^{\text {th }}$ Bohr Orbit is given by
$
\begin{aligned}
& m v r=\frac{n h}{2 \pi} \\
& \Delta L=4\left(\frac{h}{2 \pi}\right)-2\left(\frac{h}{2 \pi}\right)=\frac{h}{\pi} \\
& \Delta L=\frac{6.626 \times 10^{-34}}{3.14}=2.2 \times 10^{-34}
\end{aligned}
$
Hence, the answer is the option (2).
Example 2: Which of the following statements is incorrect for Bohr's model of an atom?
1) (correct) It is valid for a multi-electronic species
2) Angular momentum of an electron is quantized
3) The centripetal force of attraction required for circular motion is provided by the electrostatic force of attraction between the electron and the nucleus
4) Orbits have fixed energy and are referred to as stationary states
Solution
Bohr's model is valid for only electronic species.
All other given statements given in the options are correct.
Hence, the answer is the option (1).
Example 3: The de-Broglie wavelength of a particle of mass 6.63 g moving with a velocity of $100 \mathrm{~ms}^{-1}$ is:
1) (correct) $10^{-33} \mathrm{~m}$
2) $10^{-35} \mathrm{~m}$
3) $10^{-31} \mathrm{~m}$
4) $10^{-25} \mathrm{~m}$
Solution
As discussed in concept:
De-Broglie wavelength:
$
\begin{aligned}
& \lambda=\frac{h}{m v}=\frac{h}{p} \\
& \text { - wherein }
\end{aligned}
$
where $m$ is the mass of the particle
V: its velocity
p: its momentum
So,
$
\begin{aligned}
& \lambda=\frac{6.625 \times 10^{-34}}{6.63 \times 10^{-3} \times 100} \\
& \lambda=10^{-33} \mathrm{~m}
\end{aligned}
$
Hence, the answer is the option (1).
Example 4: The electronic configuration of copper is:
1) (correct) $[\operatorname{Ar}] 3 d^{10} 4 s^1$
2) $[\operatorname{Ar}] 3 d^9 4 s^2$
3) $[\operatorname{Ar}] 3 d^{10} 4 s^2$
4) $[\operatorname{Ar}] 3 d^8 4 s^2$
Solution
Ideally, the electronic configuration of Cu must be [Ar] $3 d^9 4 s^2$ but in this case, the electrons in d-orbitals are not symmetrically filled. Thus to maintain the symmetricity, one electron from the 4 s -orbital goes to the d-orbital and thus Cu maintains the electronic configuration as $[A r] 3 d^{10} 4 s^1$.
Also read
| Atomic Number Mass Number | Dipole Moment |
| Anions and Cations Difference | Shapes of Orbitals |
| Matter Particles Characteristics | Bohrs Model |
| Difference Between Orbit and Orbitals |
Hence, the answer is the option (1).
Conclusion
The presently accepted model for the structure of atoms is a natural outcome of earlier models, as over time, scientists tried to overcome various shortcomings faced by earlier models. There is still a huge scope of research in this field as researchers discover various particles like Quarks, Leptons, etc. These subatomic particles have many real-life applications. The revolutionary idea of the Quantum Computer is also associated with these particles only.
Frequently Asked Questions (FAQs)
Limitations of Rutherford’s model:
It couldn’t explain the stability of atoms (since accelerating electrons should emit energy and collapse into the nucleus).
It didn’t explain the line spectra of elements.
| Particle | Charge (Coulomb) | Mass (kg) |
|---|---|---|
| Electron | -1.6 × 10⁻¹⁹ | 9.1 × 10⁻³¹ |
| Proton | +1.6 × 10⁻¹⁹ | 1.67 × 10⁻²⁷ |
| Neutron | 0 | 1.67 × 10⁻²⁷ |
Bohr proposed (1913) that electrons orbit the nucleus in fixed, circular paths called stationary orbits (or shells) without radiating energy. Each orbit corresponds to a specific energy level.
Bohr’s main postulates:
- Electrons move in quantized orbits with fixed angular momentum: $L=n \frac{h}{2 \pi}$ (where n = orbit number).
Energy is emitted/absorbed when electrons jump between orbits ( $\Delta E=h \nu$ )
Orbits are stable ("stationary states")—no energy loss while in an orbit.
Proposed that atoms have a dense, positively charged nucleus with electrons orbiting around it (based on the gold foil experiment).
Also Read
05 Jun'25 12:48 AM