Addition Table
A mathematical table used to specify an addition and subtraction for an algebraic system is known as an addition table in mathematics. Due to its importance in laying the groundwork for operations with core numbers, the decimal addition table has historically been a key component of elementary mathematics instruction all over the globe. Many teachers think it's important for kids to learn the tables up to 10 or 20. The process of adding two or more integers together to create the addition table is known as "arithmetic addition," and the math symbol used to indicate an addition operation is a plus sign. It's "+" there. for example in the case, \[8+8=16\] ![]()
This Story also Contains
- What does Addition Table mean?
- Addition Table 1 to 10
- Explanation of Addition Table Charts 1 to 10
- Presentation of the Addition Table Chart
- Simple and Quick Addition Methods to Remember
What does Addition Table mean?
The summary of two or more values is what is referred to as an addition operation. The very same number sets are placed in the first row and the first column of an organization of numbers in a table form known as an addition table. By merely watching the pattern, the addition table enables us to immediately determine the outcome of the addition of two numbers. The addition arithmetic operation that was used to make the addition table is denoted by (+). Addends are the integers that are being added to fill the addition chart. We will use the logic of adding numbers to complete a specific row of an addition table, keeping one of the addends fixed and adjusting the other addend to Complete each entry in the corresponding row, for example, \[2+2=4,2+3=5,2+4=6\] ![]() , and so onto. The addition table also goes by the name of the addition chart.
, and so onto. The addition table also goes by the name of the addition chart.
Addition Table 1 to 10
By combining an integer from the top single row with a number from the left-most column, the addition chart employs the addition operation to complete all of the matching row values within the table. Let's look at the addition chart for numbers 1 through 10 in the chart beneath.
+ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 |
8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 |
10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Explanation of Addition Table Charts 1 to 10
Table 1 - 10: Overview of the addition table in an addition chart, we select the first addend from the group of numbers placed in the left-hand column to complete a particular row, and we continuously update the second addend that is displayed vertically in the top section. The related addend value changes each time we update a row, and this cycle continues for each of the 10 rows, from row 1 to row 10.
We'll check a few examples in order to understand the addition chart. The first part of the numbers written in the left - hand column will remain 1; the first component of the reference numbers in the top section will be changed as follows:\[1+1=2,1+2=3,1+3=4,1+4=5,1+5=6,1+6=7,1+7=8,1+7=9,1+9=10,\,\,\And 1+10=11\]
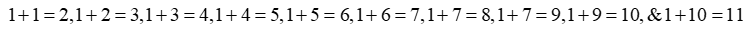 . Therefore, the numbers on the first column will be \[2,3,4,5,6,7,8,9,10,11\]
. Therefore, the numbers on the first column will be \[2,3,4,5,6,7,8,9,10,11\] 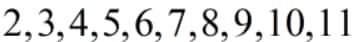
As the second element of the left-hand column, we will utilize the first addend, which is 2, to complete in the second row. We will then continue to change the 2nd addend horizontally as follows:\[2+1=3,2+2=4,2+3=5,2+4=6,2+5=7,2+6=8,2+7=9,2+8=10,2+9=11,\text{ }and\text{ }2+10=12\]
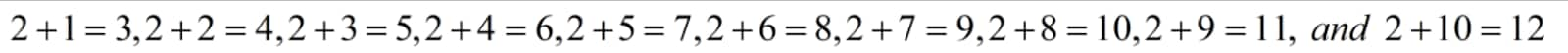 . Therefore, the entries in the second row will be \[3,\text{ }4,\text{ }5,\text{ }6,\text{ }7,\text{ }8,\text{ }9,\text{ }10,\text{ }11,\text{ }and\text{ }12\]
. Therefore, the entries in the second row will be \[3,\text{ }4,\text{ }5,\text{ }6,\text{ }7,\text{ }8,\text{ }9,\text{ }10,\text{ }11,\text{ }and\text{ }12\] 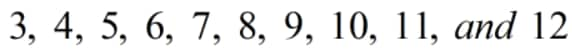
To identify the outcome of \[6+9\] ![]() on the addition table chart, we will now employ experience. The result 15, which is displayed in the addition table, is obtained by moving across the 9th column and down the 6th row. However, we are aware that addition abides with the quadratic formula. Therefore, \[6+9\,\text{ is}\,\,9+6\]
on the addition table chart, we will now employ experience. The result 15, which is displayed in the addition table, is obtained by moving across the 9th column and down the 6th row. However, we are aware that addition abides with the quadratic formula. Therefore, \[6+9\,\text{ is}\,\,9+6\] ![]() . The row and column to be examined can then be switched around as a result. We can continue across the 6-numbered column and down the 9-numbered row. If we utilise the appropriate value, the result at the connection location will still be 15. As a result, we can conclude that the rows and columns are equivalent for the addends when reading an addition table.
. The row and column to be examined can then be switched around as a result. We can continue across the 6-numbered column and down the 9-numbered row. If we utilise the appropriate value, the result at the connection location will still be 15. As a result, we can conclude that the rows and columns are equivalent for the addends when reading an addition table.
Scroll down to the row with the number 10 and move across the column that contains the same number 10 to discover the value of\[10+10\] ![]() . The junction of such digits on the addition chart shows the entry as 20.
. The junction of such digits on the addition chart shows the entry as 20.
Presentation of the Addition Table Chart
By checking at the intersection of the appropriate rows and columns of the two addends, we can quickly determine the sum of two numbers. Here are separate addition tables for each of the digits 1 - 10, which are used to fill the rows of the addition table chart.
Table of Addition for 1 |
1+1=2 |
2+1=3 |
3+1=4 |
4+1=5 |
5+1=6 |
6+1=7 |
7+1=8 |
8+1=9 |
9+1=10 |
10+1=11 |
Table of Addition for 2 |
1+2=3 |
2+2=4 |
3+2=5 |
4+2=6 |
5+2=7 |
6+2=8 |
7+2=9 |
8+2=10 |
9+2=11 |
10+2=12 |
Table of Addition for 3 |
1+3=4 |
2+3=5 |
3+3=6 |
4+3=7 |
5+3=8 |
6+3=9 |
7+3=10 |
8+3=11 |
9+3=12 |
10+3=13 |
Table of Addition for 4 |
1+4=5 |
2+4=6 |
3+4=7 |
4+4=8 |
5+4=9 |
6+4=10 |
7+4=11 |
8+4=12 |
9+4=13 |
10+4=14 |
Table of Addition for 5 |
1+5=6 |
2+5=7 |
3+5=8 |
4+5=9 |
5+5=10 |
6+5=11 |
7+5=12 |
8+5=13 |
9+5=14 |
10+5=15 |
Table of Addition for 6 |
1+6=7 |
2+6=8 |
3+6=9 |
4+6=10 |
5+6=11 |
6+6=12 |
7+6=13 |
8+6=14 |
9+6=15 |
10+6=16 |
Table of Addition for 7 |
1+7=8 |
2+7=9 |
3+7=10 |
4+7=11 |
5+7=12 |
6+7=13 |
7+7=14 |
8+7=15 |
9+7=16 |
10+7=17 |
Table of Addition for 8 |
1+8=9 |
2+8=10 |
3+8=11 |
4+8=12 |
5+8=13 |
6+8=14 |
7+8=15 |
8+8=16 |
9+8=17 |
10+8=18 |
Table of Addition for 9 |
1+9=10 |
2+9=11 |
3+9=12 |
4+9=13 |
5+9=14 |
6+9=15 |
7+9=16 |
8+9=17 |
9+9=18 |
10+9=19 |
Table of Addition for 10 |
1+10=11 |
2+10=12 |
3+10=13 |
4+10=14 |
5+10=15 |
6+10=16 |
7+10=17 |
8+10=18 |
9+10=19 |
10+10=20 |
Simple and Quick Addition Methods to Remember
A table presentation of integers in rows and columns called an addition table enables us to find the sum of two numbers visually rather than mathematically.
When adding a large list of numbers, it is easiest to do the addition process after organising the numbers into columns.
When two even numbers are added together, the outcome is also an even number, as in the case of\[4+6=10\]
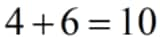 .
.In the following list, adding 0 to a number has no impact:\[2+0=2,9+0=9,\text{ }and\text{ }93+0=93\]
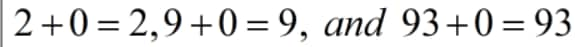 .
.When we add one to an even number, the outcome is a new number; for example:\[6+1=7\]
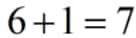 .
.No matter what order or sequence the numbers are in, when we add them together, the result is always 15. For example: \[5+4+6=15\text{ }and\text{ }3+7+5+=15\]
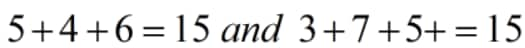
Frequently Asked Questions (FAQs)
For addition, in the first grade, students combine single-digit and double-digit numbers. Additionally, they take 10s and one-digit numerals out. Children practise more challenging addition and subtraction in the second grade. They also start studying "borrowing," or regrouping.
A device that can be used to determine the sum of two values in a table is an additional table. It can support education and learning. Any of the 100 addition facts produced by multiplying the digits 1 through 10 can be found in the table.
In order to interpret the addition table, we must first look at the addends that are supplied and then follow them across the column and down the row to the junction in the table. For instance, to find the sum of 2 and 4, we move down the row to the number 2 and across the column to the number 4. The intersection of the addition table will give us 6, which is the outcome. By moving 2 down the row and 6 across the column, the entire procedure can be reversed because addition is commutative. We will still get the same outcome from this.
The following are the four key principles of addition:
Associated property
Property that is distributed.
Equational property
Additivity in identity property.
The addition table taught to a child by:
Use dependable manipulatives to introduce the concept. It will be much simpler to make addition practical and understandable by employing numerical manipulatives.
The switch to visuals
Count on a number line.
Adding up.
Collecting the ten.
Word puzzles
Recall the math formulas.