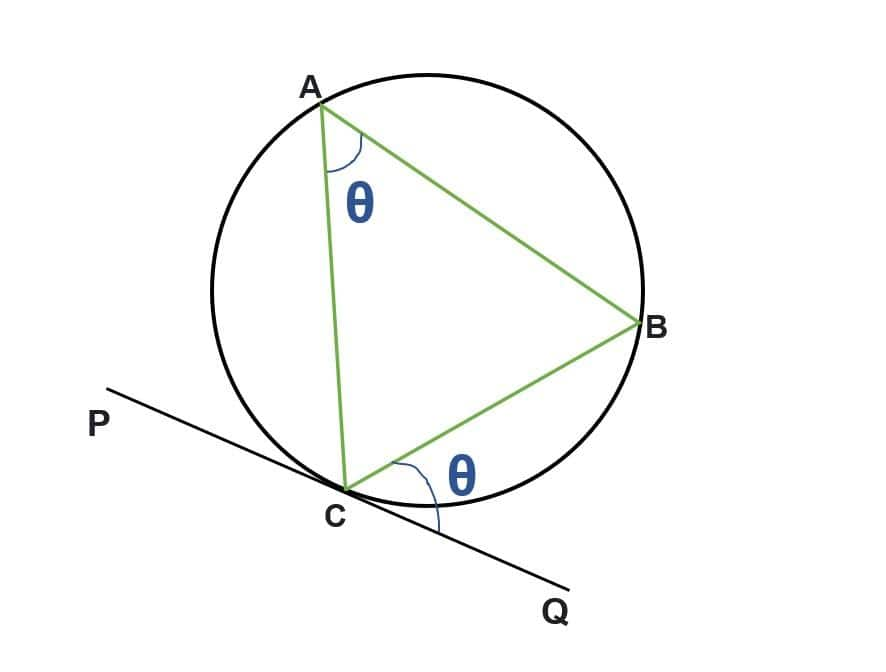
Alternate Segment Theorem (Statement, Proof and Examples)

Alternate Segment Theorem

Edited By Team Careers360 | Updated on Jul 02, 2025 05:16 PM IST

“The angle that lies between the tangent and the chord is always equal to the angle subtended by the same chord in the alternate segment”

Mathematics may serve as a universal language since it is the same everywhere. No matter what language it is accompanied by, a phrase or formula has the same meaning. It consists of many important formulas, theorems, proofs, etc., one of which is the alternate segment theorem, this theorem is related to the circle.

This Story also Contains

The Segment Of A Circle
The Chord Of A Circle
Theorems Related To Circles
Alternate Segment Theorem
Application Of Alternate Segment Theorem

Alternate Segment Theorem

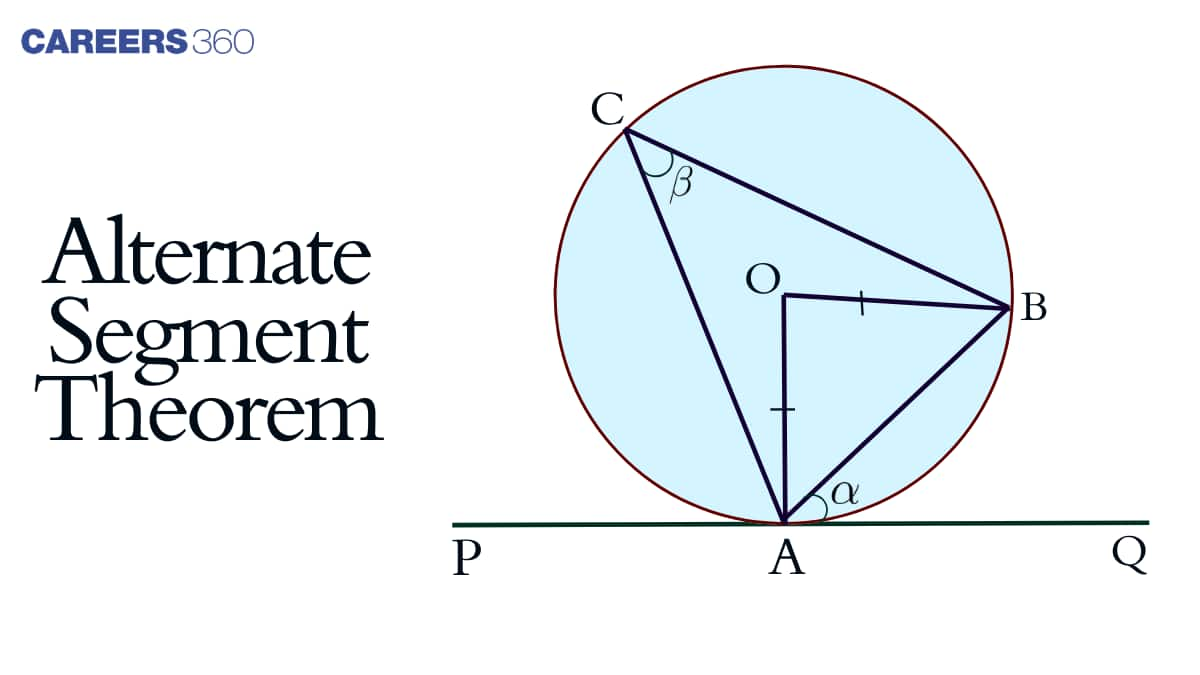
In mathematics, the circle is a two-dimensional closed shape with all points on its surface having equal distances from its center and the region of a circle between a chord and its corresponding arc is called a segment. A major segment and a minor segment can be formed in the circle when a chord is drawn to it. The alternate segment theorem is one of the important circle theorems, which states that "the angle that lies between the tangent and the chord is always equal to the angle subtended by the same chord in the alternate segment."

The Segment Of A Circle

The segment of a circle can be defined as the portion or area between the chord of the circle and the corresponding arc of the circle. When a chord is drawn, two segments are formed, i.e., the minor segment and the major segment.

Major Segment: Major Segment can be defined as the area of the circle that is enclosed between a chord and its corresponding major arc.
Minor Segment: Minor Segment can be defined as the area of the circle that is enclosed between a chord and its corresponding minor arc.

The Chord Of A Circle

The line segment joining any two points on a circle’s circumference, then that line segment can be called as the chord of the circle. The diameter is the longest chord of any circle, which always passes through its center.

The Tangent Of A Circle

A line that touches the circumference of the circle only once and never enters inside that circle can be called the "tangent to the circle."

Let us understand this by taking an example: Imagine a bike moving on a road. The bike's wheel is shaped like a circle, and one point of the wheel is always in contact with the road. So here, the road can be considered the tangent of the wheel of the bike.

In the given figure, the red line represents the tangent to the circle.

Theorems Related To Circles

Circle theorems are characteristics that reveal connections between angles in a circle's geometry. These theorems allow us to calculate missing angles without a protractor by combining them with knowledge of other angle attributes. This has a lot of applications in engineering and design.

Alternate Segment Theorem

The alternate segment theorem states that “for every circle, the angle that lies between the tangent and the chord is always equal to an angle subtended by the same chord in the alternate segment."

This theorem is also known as the tangent-chord theorem because this property of the circle is related to the tangent of the circle and chord of the circle.

In the given figure, PQ is tangent to the circle and Chord CB subtends the ∠CAB which is equal to the ∠BCQ.

Application Of Alternate Segment Theorem

It can be used to solve problems related to the circles.
It can be used when there is a chord of the circle, a tangent is passing through one of the endpoints of the chord, and the angles that are used in the question are the angle between the chord and the tangent and the angle subtended by the chord in the alternate segment.
It can help to reduce a lot of large calculations and helps to reach an easy solution for the question.

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Frequently Asked Questions (FAQs)

1. Explain Segment of a Circle.

The region between the chord and the corresponding arc of the circle is known as the circle segment. Two segments, a minor segment, and a major segment are created when a chord is drawn.

2. What is the Alternate Segment Theorem?

The alternate segment theorem states that “For every circle, the angle subtended by the chord in the alternate segment is always equal to the angle subtended by the tangent of the circle across the point of contact of the tangent." This theorem is also known as the tangent-chord theorem.

3. What is the Alternate Segment Theorem?

The Alternate Segment Theorem states that the angle between a tangent and a chord at the point of contact is equal to the angle in the alternate segment. This theorem provides a powerful relationship between angles formed by tangents and chords in a circle.

4. What is an Alternate Segment?

A chord will form two segments when it is drawn in a circle: a major segment and a minor segment. The alternate segment is part of the segment created by that specific chord and that particular arc that is on the other side of the other segment.

5. How are alternate segment theorems helpful?

The problem relating to the circle and its angle can be easily solved using an alternate segment theorem, which reduces the number of calculations required. The student won't need to apply as many other theorems because, in the absence of the alternate segment theorem, it would be necessary to apply a number of other theorems and properties, such as the cyclic quadrilateral theorem and the angle sum property of triangles, just to determine the values of intermediate angles. There would also be a number of additional calculations required to arrive at the final result.

6. Explain why the alternate segment theorem is also called the Tangent chord theorem.

Because this theorem is related to the angle subtended by the tangent of the circle and chord of the circle, i.e alternate segment theorem says that, For every circle, the angle subtended by the chord in the alternate segment is always equal to the angle subtended by the tangent across the point of contact of the tangent.

7. Can you explain what "alternate segment" means in this context?

In the Alternate Segment Theorem, the "alternate segment" refers to the smaller of the two parts of the circle divided by the chord. It's the segment on the opposite side of the chord from the tangent-chord angle being considered.

8. Is the Alternate Segment Theorem applicable to all circles?

Yes, the Alternate Segment Theorem is applicable to all circles, regardless of their size or position. It's a universal property of circles that holds true as long as the necessary elements (tangent, chord, and alternate segment) are present.

9. How can you prove the Alternate Segment Theorem?

The Alternate Segment Theorem can be proved using other circle theorems, particularly the theorem stating that the angle between a tangent and radius at the point of contact is 90°, and the theorem about angles in the same segment being equal. The proof involves constructing additional lines and applying these related theorems.

10. Can the Alternate Segment Theorem be used to find the measure of tangent-chord angles?

Yes, the Alternate Segment Theorem can be used to find tangent-chord angles. If you know the measure of the angle in the alternate segment, you can directly determine the measure of the tangent-chord angle, as they are equal according to the theorem.

11. How does the Alternate Segment Theorem relate to circle geometry?

The Alternate Segment Theorem is a fundamental concept in circle geometry. It connects tangent-chord angles with inscribed angles, providing a way to analyze and solve problems involving circles, tangents, and chords.

12. What are the key elements needed to apply the Alternate Segment Theorem?

To apply the Alternate Segment Theorem, you need a circle, a tangent line touching the circle at a point, and a chord drawn from that point. The theorem relates the angle between the tangent and chord to the angle in the alternate segment formed by the chord.

13. How does the Alternate Segment Theorem differ from the Tangent-Secant Theorem?

While both theorems involve tangents and chords, the Alternate Segment Theorem relates a tangent-chord angle to an inscribed angle in the alternate segment. The Tangent-Secant Theorem, on the other hand, relates the products of lengths of tangent and secant line segments.

14. Why is the Alternate Segment Theorem useful in solving geometric problems?

The Alternate Segment Theorem is useful because it provides a direct relationship between tangent-chord angles and inscribed angles. This allows for efficient solving of problems involving these elements, especially when other angle relationships in circles are also applied.

15. What's the relationship between the Alternate Segment Theorem and the theorem about angles in the same segment?

These theorems are closely related. The theorem about angles in the same segment states that angles in the same segment are equal. The Alternate Segment Theorem extends this concept by relating the tangent-chord angle to the angle in the alternate segment, which is essentially an angle in the same segment as the tangent-chord angle.

16. How does the Alternate Segment Theorem relate to the concept of circle tangency?

The Alternate Segment Theorem is fundamentally about tangency, as it involves the angle between a tangent and a chord. It provides a way to relate this tangency angle to an angle within the circle, thereby connecting the concepts of tangency and inscribed angles.

17. Can the Alternate Segment Theorem be extended to ellipses or other conic sections?

The Alternate Segment Theorem as stated applies specifically to circles. While similar relationships may exist for other conic sections, they would need to be separately derived and may not have the same simple form as the circle case.

18. How can you use the Alternate Segment Theorem to solve problems involving circular arcs?

The Alternate Segment Theorem can be used to relate the angle of a tangent-chord to the angle subtended by the arc in the alternate segment. This can be particularly useful in problems involving the calculation of arc lengths or areas of circular sectors.

19. What's the significance of the Alternate Segment Theorem in the broader context of Euclidean geometry?

The Alternate Segment Theorem is a key result in Euclidean geometry, specifically in the study of circles. It exemplifies the elegant relationships that exist in circle geometry and serves as a powerful tool in geometric proofs and problem-solving, showcasing the interconnectedness of geometric concepts.

20. Can the Alternate Segment Theorem be used to find the equation of a tangent line to a circle?

While the Alternate Segment Theorem doesn't directly provide the equation of a tangent line, it can be used in conjunction with other methods to verify if a given line is tangent to a circle. The angle relationship it describes can serve as a check for tangency.

21. How does the Alternate Segment Theorem contribute to the understanding of circle geometry as a whole?

The Alternate Segment Theorem is a key piece in the puzzle of circle geometry. It provides a unique relationship between tangents, chords, and inscribed angles, complementing other circle theorems. Together, these theorems form a comprehensive framework for analyzing and solving problems involving circles.

22. How does the Alternate Segment Theorem compare to the Inscribed Angle Theorem?

Both theorems relate to angles in circles, but they describe different relationships. The Inscribed Angle Theorem states that an inscribed angle is half the central angle subtending the same arc. The Alternate Segment Theorem, however, equates the tangent-chord angle to the angle in the alternate segment.

23. How does the Alternate Segment Theorem relate to the theorem about tangents from an external point?

While these theorems deal with different aspects of circle geometry, they can be used together in problem-solving. The theorem about tangents from an external point states that these tangents are equal in length, which can be useful in conjunction with the Alternate Segment Theorem when dealing with problems involving multiple tangents and chords.

24. What common misconceptions do students have about the Alternate Segment Theorem?

Common misconceptions include confusing the alternate segment with the major segment, assuming the theorem applies to secants instead of tangents, or thinking that the tangent-chord angle is equal to the inscribed angle in the same segment rather than the alternate segment.

25. How can you visually identify the angle described by the Alternate Segment Theorem?

The angle described by the Alternate Segment Theorem is formed between the tangent line and the chord at their point of intersection on the circle. This angle is equal to the angle formed by the chord and the circle in the alternate (smaller) segment.

26. Can the Alternate Segment Theorem be applied when the chord becomes a diameter?

Yes, the Alternate Segment Theorem still applies when the chord becomes a diameter. In this case, the alternate segment becomes a semicircle, and the angle in the alternate segment (semicircle) is always 90°. This aligns with the fact that the angle between a tangent and a diameter at the point of contact is always 90°.

27. How does the Alternate Segment Theorem relate to the concept of cyclic quadrilaterals?

The Alternate Segment Theorem can be useful in problems involving cyclic quadrilaterals. For instance, if a tangent is drawn at one vertex of a cyclic quadrilateral, the theorem can help relate the tangent-chord angle to angles within the quadrilateral, aiding in angle calculations.

28. Can the Alternate Segment Theorem be used to construct tangents to a circle?

While the Alternate Segment Theorem itself doesn't provide a method for constructing tangents, understanding the theorem can aid in verifying whether a constructed line is indeed tangent to a circle, by checking if it satisfies the angle relationship described by the theorem.

29. Is there a way to remember the Alternate Segment Theorem easily?

A helpful way to remember the Alternate Segment Theorem is to think "tangent-chord angle equals alternate segment angle." Visualizing a tangent "bouncing" off the circle into the alternate segment can also aid memory.

30. How can the Alternate Segment Theorem be used in real-world applications?

The Alternate Segment Theorem has applications in fields like engineering and design where circular shapes are involved. For example, it can be used in designing road curves, circular structures, or in optics when dealing with reflection off curved surfaces.

31. What's the historical significance of the Alternate Segment Theorem?

The Alternate Segment Theorem has been known since ancient times and was included in Euclid's Elements. It represents an important relationship in circle geometry that has been utilized in mathematical proofs and problem-solving for centuries.

32. How does the Alternate Segment Theorem relate to the concept of circle inversion?

While the Alternate Segment Theorem and circle inversion are distinct concepts, both deal with properties of circles that remain invariant under certain transformations. Understanding the Alternate Segment Theorem can be helpful when working with more advanced topics like circle inversion.

33. How does the Alternate Segment Theorem help in understanding the behavior of light reflection?

The Alternate Segment Theorem is relevant to understanding light reflection off curved surfaces. The angle relationship it describes is analogous to the law of reflection, where the angle of incidence equals the angle of reflection. This makes it useful in fields like optics and the design of reflective surfaces.

34. What's the connection between the Alternate Segment Theorem and the concept of power of a point with respect to a circle?

While these are distinct concepts, both the Alternate Segment Theorem and the power of a point theorem provide relationships between lines (tangents or secants) and points relative to a circle. Understanding both can enhance problem-solving skills in circle geometry.

35. Is there a version of the Alternate Segment Theorem for three-dimensional geometry?

The Alternate Segment Theorem as typically stated applies to two-dimensional circle geometry. While similar principles may apply to spheres or other three-dimensional curved surfaces, they would be considered separate theorems with their own specific statements and proofs.

36. Can the Alternate Segment Theorem be used to prove other circle theorems?

Yes, the Alternate Segment Theorem can be used as a stepping stone to prove other circle theorems. For example, it can be used in proofs involving relationships between tangents and chords, or in demonstrating properties of cyclic quadrilaterals.

37. How does the Alternate Segment Theorem help in understanding the concept of angle bisectors in circles?

While not directly related to angle bisectors, the Alternate Segment Theorem can be used in conjunction with theorems about angle bisectors in circles. For instance, it can help in problems where a tangent-chord angle needs to be related to an angle bisector of a cyclic quadrilateral.

38. How can the Alternate Segment Theorem be used in constructing proofs about cyclic quadrilaterals?

The Alternate Segment Theorem can be valuable in proofs involving cyclic quadrilaterals, especially when tangents are involved. It provides a way to relate external angles (formed by tangents) to internal angles of the quadrilateral, which can be crucial in establishing or proving properties of these shapes.

39. What role does the Alternate Segment Theorem play in the study of circle theorems?

The Alternate Segment Theorem is a fundamental result in the study of circle theorems. It bridges the concepts of tangents and inscribed angles, providing a key relationship that is often used in conjunction with other circle theorems to solve complex geometric problems.

40. How can the Alternate Segment Theorem be applied in problems involving intersecting circles?

In problems with intersecting circles, the Alternate Segment Theorem can be applied to each circle individually. This can be particularly useful when dealing with common tangents to two circles, as it provides relationships between tangent-chord angles and inscribed angles in each circle.

41. How does the Alternate Segment Theorem relate to the concept of inscribed and circumscribed circles?

The Alternate Segment Theorem primarily deals with a single circle, but it can be useful in problems involving inscribed or circumscribed circles. For instance, when a triangle is inscribed in a circle, the theorem can help relate angles formed by the sides of the triangle (which are chords of the circle) to angles formed by tangents at the vertices.

42. What's the importance of the Alternate Segment Theorem in competitive mathematics?

In competitive mathematics, the Alternate Segment Theorem is a powerful tool for solving complex geometry problems efficiently. Its simple yet profound relationship often provides a key insight or shortcut in multi-step problems involving circles, tangents, and chords.

43. How can the Alternate Segment Theorem be used to solve problems involving the area of circular segments?

The Alternate Segment Theorem can be helpful in problems involving circular segments. By relating the tangent-chord angle to the angle in the alternate segment, it can provide a way to calculate angles needed for determining the area of a segment, especially when combined with trigonometric methods.

44. What's the connection between the Alternate Segment Theorem and the properties of cyclic quadrilaterals?

The Alternate Segment Theorem can be particularly useful when dealing with cyclic quadrilaterals that have a side tangent to the circumcircle. In such cases, the theorem provides a direct relationship between this external tangent-chord angle and an internal angle of the quadrilateral, aiding in angle calculations and proofs.

45. Can the Alternate Segment Theorem be generalized or extended to other geometric shapes?

The Alternate Segment Theorem is specific to circles due to their unique properties. While similar relationships might exist for other curves, they would need to be separately derived and would likely not have the same simple form. The theorem showcases the special nature of circles in geometry.