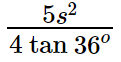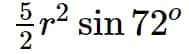Area of a Pentagon: Formula, Definition, and Examples
The region that is surrounded by a pentagon's five sides is known as the area of the pentagon. Various techniques can be used to compute it depending on the dimensions that are known. The type of pentagon is another factor. The area of a pentagon is represented in square units. A pentagon's area is calculated using its sides and apothem length.
This Story also Contains
- What Is A Pentagon?
- The Formula For Calculating The Area Of A Pentagon
- Types Of Pentagons
- Perimeter Of Pentagon
- Properties Of Pentagon
What Is A Pentagon?
A pentagon is a five-sided polygon and a two-dimensional geometrical shape. Its shape could be basic or self-intersecting. In the Pentagon, there are five equal angles. The Greek words "Penta" (which means "five") and "gon" (which means "angles") are the origin of its name.
Apothem - A pentagon's apothem is a line segment traced perpendicular to one of its sides from the pentagon's center.
The distance between a pentagon's center to one of its vertices is known as the radius.
Commonly Asked Questions
Q: What's the connection between the area of a pentagon and the concept of a characteristic function in measure theory?
A:
The characteristic function of a pentagon (which is 1 inside the pentagon and 0 outside) can be used to express its area as an integral over the entire plane. This approach connects area calculation to more abstract concepts in measure theory and functional analysis.
The Formula For Calculating The Area Of A Pentagon
The formula for finding the area of a regular pentagon that is frequently employed is,
Area of pentagon = ½ * p * a
Here, the pentagon's perimeter is represented by "p," and its apothem by "a."
By breaking up an irregular pentagon into smaller polygons, the area of the irregular pentagon can be computed. Following that, the areas of these polygons are calculated and summed to determine the pentagon's area.
If a pentagon's side length is all that is specified, then,
Area of pentagon = \frac{5s^{2}}{4\tan36^{o}}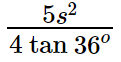 
If only the pentagon's radius is specified, then,
Area of pentagon = \frac{5}{2}r^{2}\sin72^{o}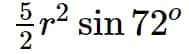 
Commonly Asked Questions
Q: What is a pentagon and why is its area important in calculus?
A:
A pentagon is a five-sided polygon. Its area is important in calculus because it demonstrates how integration can be applied to find areas of complex shapes that cannot be easily calculated using basic geometric formulas. This concept is crucial in understanding the practical applications of integral calculus.
Q: How does the formula for the area of a regular pentagon differ from that of an irregular pentagon?
A:
The formula for a regular pentagon's area is straightforward: A = (1/4)√(25+10√5)s², where s is the side length. For an irregular pentagon, there's no single formula. Instead, you'd typically divide it into triangles and use integration or the sum of triangular areas to calculate the total area. This difference highlights the versatility of calculus in handling complex shapes.
Q: What's the connection between the area of a pentagon and the concept of Riemann sums?
A:
Riemann sums are a precursor to integration, where we approximate the area under a curve by dividing it into rectangles. When finding the area of a pentagon using calculus, we're essentially taking this concept to its limit. As the number of rectangles (or trapezoids) approaches infinity, the Riemann sum becomes the definite integral, giving us the exact area of the pentagon.
Q: How does the method for finding a pentagon's area differ when using polar coordinates versus Cartesian coordinates?
A:
In Cartesian coordinates, we typically integrate the difference between two functions representing the top and bottom edges of the pentagon. In polar coordinates, we integrate r²/2 with respect to θ, where r is expressed as a function of θ. The polar method can be simpler for pentagons with rotational symmetry, while Cartesian coordinates might be easier for pentagons aligned with the x and y axes.
Q: Why might we need to use double integrals to find the area of a pentagon?
A:
Double integrals become necessary when the pentagon's boundaries are defined by complex functions that can't be easily separated into top and bottom curves. In such cases, we integrate over both x and y, effectively summing up infinitesimal rectangular areas across the entire pentagon. This method is more versatile but often more computationally intensive.
Types Of Pentagons
Pentagons can be convex or concave, regular or irregular.
Regular pentagon - The sides and angles of a regular pentagon are all equal. It has 72-degree exterior angles and 108-degree interior angles. A regular pentagon's internal angles add up to 540 degrees.
Irregular pentagon - There are no specified angles in an irregular pentagon since it lacks equal sides and/or angles.
Convex pentagon - A pentagon is said to be convex if its vertices, or points, where the sides meet, point outward. All interior angles within a convex pentagon are smaller than 180 degrees.
Concave pentagon - A pentagon is said to be concave if its vertices, or points, where the sides meet, point inward. One or more of the angles of a concave pentagon is more than 180 degrees, that is, a reflex angle.
Commonly Asked Questions
Q: Why can't we always use the simple formula A = (1/4)√(25+10√5)s² for pentagon areas in calculus problems?
A:
The simple formula only applies to regular pentagons. In calculus, we often encounter irregular pentagons or situations where we don't know the side length. Integration allows us to find areas of any pentagon shape by breaking it down into infinitesimal strips and summing them up, which is more versatile for complex problems.
Q: How does integration help in finding the area of an irregular pentagon?
A:
Integration helps by allowing us to break down the irregular pentagon into infinitesimally small vertical or horizontal strips. We can then express the area of each strip as a function of its position, integrate this function over the entire width or height of the pentagon, and sum up all these areas to get the total area of the irregular pentagon.
Q: How does the method of finding a pentagon's area change if the pentagon is defined implicitly rather than explicitly?
A:
For implicitly defined pentagons (where the boundary is given by an equation like f(x,y) = 0), we often need to use more advanced techniques. These might include implicit differentiation to find tangent lines, or using Lagrange multipliers to find extrema. This scenario demonstrates how area calculations can lead to the application of multivariable calculus techniques.
Q: How does the method for finding a pentagon's area change if the pentagon is defined on a parametric surface?
A:
For a pentagon on a parametric surface, we need to use surface integrals in parametric form. The area element becomes more complex, involving the cross product of partial derivatives of the surface parameterization. This scenario demonstrates how area calculations extend to curved spaces and connects to differential geometry.
Q: How does the method of finding a pentagon's area change if the pentagon is defined in hyperbolic or spherical geometry?
A:
In non-Euclidean geometries like hyperbolic or spherical geometry, the formulas and methods for calculating area change. We need to use the appropriate metric for the space and may need to employ techniques from differential geometry. This scenario demonstrates how the concept of area extends beyond flat Euclidean space and connects to more advanced mathematical theories.
Perimeter Of Pentagon
We are aware that the lengths of all the sides make up a pentagon's perimeter. If it is a regular pentagon, the lengths of its five sides are all equal. Consider a regular pentagon with a side length of 'a'. In this instance, the formula can be used to determine the perimeter.
Perimeter of pentagon = a+a+a+a+a = 5a
Commonly Asked Questions
Q: Why might we need to use variational calculus to find the area of a pentagon?
A:
Variational calculus might be useful if we're trying to find a pentagon with a certain area that optimizes some other property (like minimizing perimeter). The area would appear as a constraint in the variational problem. This approach demonstrates how area calculations can be part of more complex optimization problems in advanced calculus.
Q: Why might we need to use Fourier analysis techniques to find the area of a pentagon?
A:
Fourier analysis can be useful if the pentagon's boundary is defined by a periodic function. We could express the boundary as a Fourier series and then use properties of Fourier transforms to calculate the area. This approach demonstrates how techniques from signal processing and harmonic analysis can provide alternative methods for geometric calculations.
Q: What's the relationship between the area of a pentagon and the concept of a moment of inertia?
A:
While area and moment of inertia are different concepts, they're both calculated using similar integration techniques. The moment of inertia involves integrating the product of area elements and the square of their distance from an axis. Understanding this connection helps in seeing how calculus techniques for area calculation extend to other physical properties.
Q: What's the connection between the area of a pentagon and the concept of a winding number in complex analysis?
A:
The winding number in complex analysis can be related to the area of a pentagon through Green's theorem. If we treat the pentagon's boundary as a complex curve, the winding number integral around this curve is related to the area enclosed. This connection showcases how concepts from complex analysis can provide insights into real-valued problems like area calculation.
Properties Of Pentagon
The following are some of the pentagon's characteristics:
The interior angles of the pentagon add up to 540 degrees.
It is a regular pentagon if all the sides are equal and all the angles are of equal size. It is irregular if not.
Each interior angle in the regular pentagon is 108°, while each exterior angle is 72°.
Five equal sides make up an equilateral pentagon.
A rectangular pentagon's interior angles add up to 540°.
Commonly Asked Questions
Q: How does the concept of Green's Theorem relate to finding the area of a pentagon?
A:
Green's Theorem relates line integrals around a closed curve to double integrals over the enclosed region. For a pentagon, we can use Green's Theorem to convert the problem of finding area (a double integral) into a line integral around the pentagon's perimeter. This can sometimes simplify the calculation, especially for pentagons with complex boundaries.
Q: How does the concept of path independence apply to finding a pentagon's area using line integrals?
A:
Path independence is crucial when using line integrals to find a pentagon's area. It means that the result should be the same regardless of which path we choose around the pentagon's perimeter. This property is guaranteed for conservative vector fields, which is the case when we're finding area. Understanding this helps us choose the most convenient path for integration.
Q: How does the method for finding a pentagon's area change if the pentagon is rotated at an angle to the coordinate axes?
A:
If a pentagon is rotated, we have two main options: 1) Use a coordinate transformation to align the pentagon with the axes, then integrate as usual. This involves substituting x and y with expressions involving new variables. 2) Use polar coordinates, which can handle rotated shapes more naturally. The choice depends on the specific pentagon and which method leads to simpler integrals.
Q: Why might we need to use parametric equations to find the area of a pentagon?
A:
Parametric equations are useful when the pentagon's boundaries are more easily expressed as functions of a parameter rather than as direct functions of x or y. For example, if the pentagon is formed by the path of a particle, its x and y coordinates might be given as functions of time. In such cases, we can use parametric integration techniques to find the area.
Q: What's the significance of the divergence theorem in relation to finding a pentagon's area?
A:
The divergence theorem relates a surface integral over a closed surface to a volume integral over the region it encloses. While it's typically used for 3D problems, in 2D it reduces to Green's theorem, which we can use to find a pentagon's area. Understanding this connection helps in visualizing how area calculations relate to more advanced concepts in vector calculus.
Frequently Asked Questions (FAQs)
Q: How does the concept of a differential form relate to finding the area of a pentagon?
A:
Differential forms provide a coordinate-independent way to express the area element. For a pentagon, we would use a 2-form to represent the area element. This approach is particularly useful for pentagons on curved surfaces or in higher dimensions, and it provides a bridge between calculus and differential geometry.
Q: Why might we need to use techniques from algebraic geometry to find the area of a pentagon?
A:
Algebraic geometry techniques might be useful if the pentagon is defined by polynomial equations. We could use tools like Gröbner bases to simplify the equations before integration. This approach shows how area calculations can connect to more abstract algebraic structures and techniques.
Q: How does the concept of a tensor relate to finding the area of a pentagon?
A:
Tensors generalize the concept of area to higher dimensions and curved spaces. The area element of a pentagon can be thought of as a 2-tensor. In more complex scenarios, like pentagons on curved surfaces, understanding tensors becomes crucial for correctly formulating the area integral. This connection shows how area calculations link to advanced topics in differential geometry.
Q: How does the method of finding a pentagon's area change if the pentagon is defined on a Riemann surface?
A:
On a Riemann surface, which is a one-complex-dimensional manifold, area calculations become more complex. We need to use the appropriate metric on the surface and may need to employ techniques from complex analysis and differential geometry. This scenario shows how area calculations extend to more abstract mathematical structures.
Q: How does the concept of a conformal mapping relate to finding the area of a pentagon?
A:
Conformal mappings preserve angles but not necessarily areas. If we can conformally map a pentagon to a simpler shape (like a square), we can calculate the area of the simpler shape and then use the properties of the conformal map to find the original pentagon's area. This approach showcases the connections between complex analysis and geometry.
Q: How does the method for finding a pentagon's area change if the pentagon is defined in a non-Cartesian coordinate system?
A:
In non-Cartesian coordinate systems (like polar, cylindrical, or spherical coordinates), the form of the area element changes. For example, in polar coordinates, the area element is r dr dθ instead of dx dy. We need to adjust our integration accordingly, often leading to different but equivalent integrals. This scenario demonstrates the importance of understanding coordinate transformations in calculus.
Q: What role does the Fundamental Theorem of Calculus play in calculating a pentagon's area?
A:
The Fundamental Theorem of Calculus is crucial in evaluating the definite integrals we use to find a pentagon's area. It allows us to find the area by calculating the antiderivative of the integrand (which represents the width of the pentagon at each height) and evaluating it at the limits of integration. This theorem bridges the gap between the concept of area and the process of integration.
Q: What's the significance of the Stokes' theorem in relation to finding a pentagon's area?
A:
Stokes' theorem generalizes Green's theorem to three dimensions, relating a surface integral to a line integral around its boundary. While not directly applicable to 2D pentagons, understanding Stokes' theorem provides insight into how Green's theorem (which we use for pentagon areas) fits into a broader mathematical framework. It also helps in visualizing how area calculations extend to higher dimensions.
Q: What's the significance of the Jacobian determinant in calculating the area of a pentagon?
A:
The Jacobian determinant becomes important when we need to change variables in a double integral, which is often necessary for pentagons with complex boundaries. It represents the factor by which our integration transforms the area element. Understanding the Jacobian is crucial for correctly applying variable transformations in area calculations.
Q: Why might we need to use numerical integration methods to find the area of a pentagon?
A:
Numerical integration becomes necessary when the integrals involved in calculating the pentagon's area are too complex to solve analytically. Methods like Simpson's rule or the trapezoidal rule approximate the area by dividing the pentagon into many small shapes. This approach highlights the practical side of calculus, where exact solutions aren't always possible or efficient.
Articles
News and Notifications
Latest updates
Classroom Precautions During Covid-19
Aug 18, 2025
What is Mental Health For Students
Aug 18, 2025
How To Improve The Mental Health Of Students
Aug 14, 2025