Conjugates of Complex Numbers - Properties and Solved Examples
Conjugates of complex numbers are an important concept in mathematics, especially when solving problems related to division, simplification, and quadratic equations. A complex number is written in the form $a+bi$, and its conjugate is $a-bi$. Conjugates help in reducing expressions, finding modulus, and proving many properties of complex numbers. They are also useful in NCERT Class 11 and Class 12 Maths when dealing with complex algebra. In this article, we will learn the definition of conjugates of complex numbers, important properties, formulas, solved examples, and practice questions.
This Story also Contains
- Introduction to Complex Numbers
- Conjugate of a Complex Number
- Multiplication of Complex Conjugates
- Geometrical Representation of complex conjugate
- Properties of the Conjugate of Complex Numbers
- Rules and Formulas for Complex Conjugates
- List of topics related to the Conjugate of a Complex Number
- NCERT Resources
- Practice Questions based on the Conjugate of a Complex Number
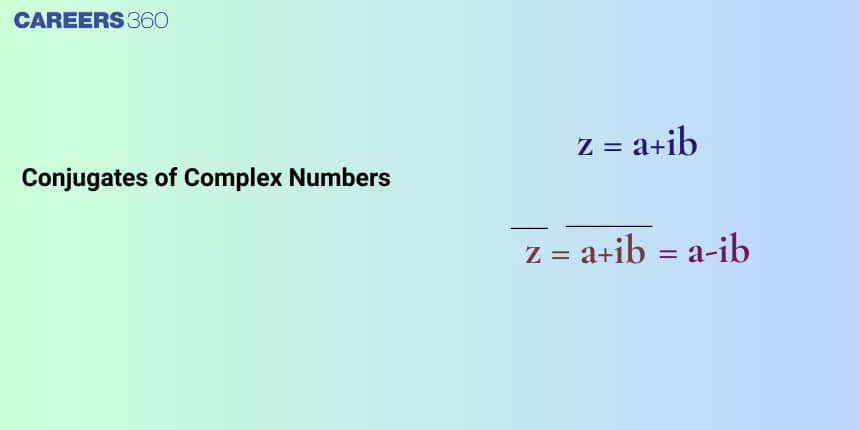
Introduction to Complex Numbers
A complex number is a number that cannot be represented on the real number line alone. The general form of a complex number is $a + ib$, where $i$ is iota or $i = \sqrt{-1}$.
A number of the form $a + ib$ is called a complex number, where $a$ and $b$ are real numbers. Complex numbers are usually denoted by $z, z_1, z_2$, etc.
Example: $z = 5 + 2i$
Real part: $\text{Re}(z) = 5$
Imaginary part: $\text{Im}(z) = 2$
Conjugate of a Complex Number
The conjugate of a complex number is formed by changing the sign of its imaginary part while keeping the real part unchanged. It is useful for simplifying expressions, performing division, and solving problems with complex numbers. Let us describe in detail the conjugate of a complex number:
Definition of Conjugate
The conjugate of a complex number is another complex number with the same real part and an imaginary part of equal magnitude but opposite sign. The conjugate of $z$ is represented by $\bar{z}$.
If $z = a + ib$, then its conjugate is: $\bar{z} = a - ib$
Together, $z$ and $\bar{z}$ form a complex-conjugate pair.
Obtaining the Conjugate
The conjugate is obtained by changing the sign of the imaginary part while keeping the real part unchanged.
Multiplication of Complex Conjugates
When a complex number is multiplied by its conjugate, the result is a real number equal to the square of the magnitude of the complex number:
$(a + ib)(a - ib) = a^2 - (ib)^2 = a^2 - i^2 b^2 = a^2 + b^2$
Example: Multiply $5 + i$ with its conjugate $5 - i$:
$(5+i)(5-i) = 5^2 - i^2 = 25 + 1 = 26$
The result is the square of the magnitude of $5 + i$.
Complex Conjugate of a Matrix
The complex conjugate of a matrix $A$ is another matrix whose entries are the conjugates of $A$’s entries.
Example: $A = [4-i, 8+2i, 9+7i]$
$\bar{A} = [4+i, 8-2i, 9-7i]$

Complex Conjugate Root Theorem
If $f(x)$ is a polynomial with real coefficients and $a + ib$ is a root, then its conjugate $a - ib$ is also a root.
Example: $f(x) = x^3 - 7x^2 + 41x - 87$
Roots: $3, 2 + 5i, 2 - 5i$
Here, $2 + 5i$ and $2 - 5i$ are conjugates of each other.
Geometrical Representation of complex conjugate
The conjugate $\bar{z}$ is the reflection of $z$ across the real axis in the complex (Argand) plane.
Example: $z = 2 + 2i \implies \bar{z} = 2 - 2i$

Properties of the Conjugate of Complex Numbers
Let $z, z_1, z_2, z_3$ be complex numbers:
$\overline{(\bar{z})} = z$
$z + \bar{z} = 2 \cdot \text{Re}(z)$
$z - \bar{z} = 2i \cdot \text{Im}(z)$
$z + \bar{z} = 0 \implies z$ is purely imaginary
$z - \bar{z} = 0 \implies z$ is purely real
$\overline{z_1 \pm z_2} = \bar{z}_1 \pm \bar{z}_2$
$\overline{z_1 \cdot z_2} = \bar{z}_1 \cdot \bar{z}_2$
$\overline{\frac{z_1}{z_2}} = \frac{\bar{z}_1}{\bar{z}_2}, \quad z_2 \neq 0$
$\overline{z^n} = (\bar{z})^n$
$z_1 \cdot \bar{z}_2 + \bar{z}_1 \cdot z_2 = 2 \text{Re}(z_1 \cdot \bar{z}_2)$
Notes:
$z + \bar{z} = 2a$ (real)
$z \cdot \bar{z} = a^2 + b^2$ (real)
Rules and Formulas for Complex Conjugates
Understanding the rules and formulas for complex conjugates is essential to simplify expressions, solve division problems, and work with polynomials in Class 11 Maths and competitive exams. Conjugates help in reducing complex numbers to real numbers and make algebraic operations easier.
General Formula for Conjugate
For any complex number $z = a + ib$, the conjugate is given by:
$\bar{z} = a - ib$
This simple formula changes the sign of the imaginary part while keeping the real part unchanged. It is the foundation for all operations involving complex conjugates.
Relation Between a Complex Number and Its Conjugate
A complex number and its conjugate have key relationships that simplify calculations:
Sum of a number and its conjugate:
$z + \bar{z} = (a + ib) + (a - ib) = 2a \quad \text{(real)}$Difference of a number and its conjugate:
$z - \bar{z} = (a + ib) - (a - ib) = 2ib \quad \text{(purely imaginary)}$Product of a number and its conjugate:
$z \cdot \bar{z} = (a + ib)(a - ib) = a^2 + b^2 \quad \text{(real)}$
These relationships are crucial for simplifying complex number division, finding modulus, and proving polynomial properties.
Using Conjugates in Simplification
Conjugates are widely used to simplify expressions involving complex numbers, especially in division and rationalization.
Example: Simplifying $\frac{1}{2 + 3i}$ using the conjugate of the denominator:
$\frac{1}{2 + 3i} \cdot \frac{2 - 3i}{2 - 3i} = \frac{2 - 3i}{2^2 + 3^2} = \frac{2 - 3i}{13}$
Here, multiplying by the conjugate converts a complex denominator into a real number, making the fraction easier to work with.
Solved Examples Based On Conjugates of Complex Numbers
Example 1: If $(a+i b)^5=p+i q$, where $i=\sqrt{-1}$ then, $(b+i a)^5=$
Solution:
Given: $(a + ib)^5 = p + iq$
Taking the conjugate of both sides, we get:
$(a - ib)^5 = p - iq$
This can be written as:
$(-i^2 a - ib)^5 = -i^2 p - iq$
Taking $-i$ common on both sides:
$(-i)^2 (ia + b)^3 = (-i)(ip + q)$
Now, $(-i)$ gets cancelled from both sides and we are left with:
$(b + ia)^5 = q + ip$
Hence, the answer is $q + ip$.
Example 2: If $(\bar{z})^3=5-7 i$ then $z^3$ equals
Solution:
We know the properties of the conjugate of a complex number:
$(\bar{z})^n = \overline{z^n}$
where $\bar{z}$ denotes the conjugate of $z$
$\bar{z}^3 = 5 - 7i$
$\overline{z^3} = 5 - 7i$
Taking the conjugate of both sides, we get:
$z^3 = 5 + 7i$
Example 3: z is a complex number such that $z+\bar{z}=5$ and $z-\bar{z}=7 i$ then z equals
Solution:
We know the properties of the conjugate of a complex number:
$\operatorname{Im}(z) = \frac{z - \bar{z}}{2i}$, where
$\operatorname{Im}(z)$ denotes the imaginary part of $z$
$\bar{z}$ denotes the conjugate of $z$
$z + \bar{z} = 5$
$z - \bar{z} = 7i$
Adding both: $2z = 5 + 7i \Rightarrow z = \frac{5}{2} + \frac{7}{2}i$
Or, using formulas: $\operatorname{Re}(z) = \frac{z + \bar{z}}{2} = \frac{5}{2}$ and $\operatorname{Im}(z) = \frac{z - \bar{z}}{2i} = \frac{7}{2}$
Hence, the answer is $z = \frac{5}{2} + \frac{7}{2}i$
Example 4: z is a complex number such that $z-\bar{z}=4 i$ , then $\operatorname{Im}(z)$ equals
Solution:
As we learned in properties of the conjugate of a complex number:
$\operatorname{Im}(z) = \frac{z - \bar{z}}{2i}$ where $\operatorname{Im}(z)$ denotes the imaginary part of $z$
$\bar{z}$ denotes the conjugate of $z$
$\operatorname{Im}(z) = \frac{z - \bar{z}}{2i} = \frac{4i}{2i} = 2$
Hence, the answer is $2$.
Solution:
As we learned in properties of the conjugate of a complex number:
$\bar{z}_1 - \bar{z}_2 = \overline{z_1 - z_2}$
where $\bar{z}$ denotes the conjugate of $z$
$\Rightarrow \overline{z_1 - z_2} = \sqrt{3} + i \Rightarrow z_1 - z_2 = \sqrt{3} - i$
Since $z_1 - z_2$ lies in the fourth quadrant, the argument is:
$\arg(z_1 - z_2) = -\tan^{-1}\left|\frac{-1}{\sqrt{3}}\right| = \frac{-\pi}{6}$
Hence, the answer is $\frac{-\pi}{6}$.
List of topics related to the Conjugate of a Complex Number
Below is a list of topics related to the conjugate of a complex number, including its definition, key properties, formulas, and solved examples. These topics will help students clearly understand how conjugates simplify complex number operations and their importance in mathematics.
NCERT Resources
Below are the NCERT resources for Class 11 Maths Chapter 5 – Complex Numbers and Quadratic Equations, which include NCERT solutions, exemplar questions, and detailed notes. These resources provide step-by-step explanations to help students practice conjugates of complex numbers, properties, and solved examples effectively.
NCERT Solutions for Class 11 Maths Chapter 5 -Complex Numbers and Quadratic Equations
NCERT Exemplar Class 11 Maths Solutions for Chapter 5 - Complex Numbers and Quadratic Equations
NCERT Class 11 Maths Notes for Chapter 5 - Complex Numbers and Quadratic Equations
Practice Questions based on the Conjugate of a Complex Number
Below are some practice questions based on the conjugate of a complex number, designed to strengthen understanding of its properties, formulas, and applications. Solving these problems will help students master conjugates of complex numbers and prepare effectively for exams.
Conjugates Of Complex Numbers - Practice Question MCQ
We have shared practice questions sets for related topics below:
Frequently Asked Questions (FAQs)
A complex number is a number of the form $a + ib$, where $a$ is the real part and $b$ is the imaginary part. Example: $5 + 2i$.
Key properties of complex conjugates include:
$z + \bar{z} = 2 \operatorname{Re}(z)$ (real)
$z - \bar{z} = 2i \operatorname{Im}(z)$ (purely imaginary)
$z \cdot \bar{z} = |z|^2 = a^2 + b^2$ (real)
$\overline{z_1 \pm z_2} = \bar{z}_1 \pm \bar{z}_2$
$\overline{z_1 \cdot z_2} = \bar{z}_1 \cdot \bar{z}_2$
$\overline{(z_1/z_2)} = \bar{z}_1 / \bar{z}_2$ (for $z_2 \neq 0$)
If z is purely real, then z̄ = z.