Permutation and Combinations - Topics, Formula, Books, FAQs
Permutations and Combinations help us determine the number of different ways to arrange or select objects from a set without listing all possibilities. For example, if you have a rack of books of different genres, permutations allow you to find all possible arrangements of the books, while combinations help you determine how many ways you can select certain genres. This concept forms an important part of class 11 mathematics and is frequently asked in questions in many competitive exams. In this article, we will explore permutation and combinations formula, tricks, key concepts, and practice questions to master this topic efficiently.
This Story also Contains
- What is factorial?
- What are the Fundamental Principles of Counting?
- What is Permutation?
- Types of Permutations
- What is the Combination?
- Relation between Permutation and Combination
- Difference between Permutation and Combination
- Questions based on Permutation and Combination
- List of topics related to Permutations and Combinations according to JEE MAIN/NCERT
- Best Books and resources for Permutations and Combinations
- Practice Questions based on Permutations and Combinations
What is factorial?
A factorial is the product of all positive integers up to a given number.
It is denoted by $n!$.
$n!=n ×(n-1)×(n-2)×(n-3)×………×2 ×1$
It is calculated as follows.
$6! = 6 × 5 × 4 × 3 × 2 × 1 = 720$
Note that:
$1! = 1$
$0! = 1$
What is the meaning of $n!$?
$n!$ is read as “$n$ factorial”. It represents the products all positive integers from $1$ to $n$.
$n! = n × (n -1) × (n - 2) × (n - 3) × . . . . . . . × 1$
It is used in various mathematical and real-world contexts like:
Permutations and combinations
In calculations involving probability distributions.
Algebra and calculus
Computer science algorithms involving combinatorial logic.
What are the Fundamental Principles of Counting?
Fundamental Principle of Counting rules used to count the number of ways certain arrangements can occur.
It has two types.
Principle of Addition
Principle of Multiplication
Principle of Addition(OR rule)
If work $W$ can be completed by doing task $A$ OR task$ B$, and $A$ can be done in $m$ ways and $B$ can be done in $n$ ways (and both cannot occur simultaneously: in this case, we call tasks $A$ and $B$ as mutually exclusive), hen work $W$ can be done in $(m+n)$ ways.
Principle of Multiplication(AND rule)
If a certain work $W$ can be completed by doing $2$ tasks, first doing task and then doing task $B$. A can be done in $m$ ways and following that $B$ can be done in $n$ ways, then the number of ways of doing the work $W$ is $(m \times n)$ ways.
What is Permutation?
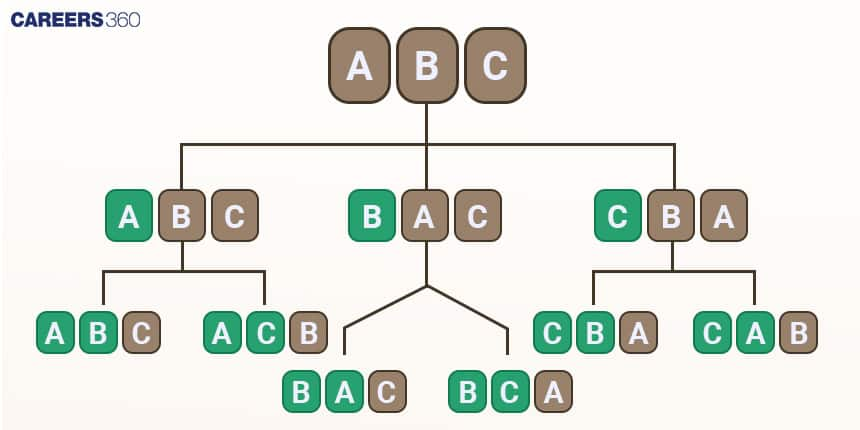
A permutation is an arrangement of all or part of a set of objects where order matters. Arranging $n$ objects in $r$ places means filling $r$ positions with $n$ distinct objects. For example, with letters $A, B, C$, the number of ways to arrange $2$ letters is $6$: $AB, AC, BA, BC, CA, CB$. Here, $n=3$ and $r=2$ show how permutations count ordered selections from $n$ objects taken $r$ at a time.
What is the formula for Permutation?
Arranging $n$ objects in $r$ places (Same as arranging $n$ objects taken $r$ at a time) is equivalent to filling $r$ places from $n$ things.

So the number of ways of arranging $n$ objects taken $r$ at a time $=n(n-1)$
$
\begin{aligned}
& (n-2) \ldots(n-r+1) \\
& \frac{n(n-1)(n-2) \ldots(n-r+1)(n-r)!}{(n-r)!}=\frac{n!}{(n-r)!}={ }^n P_r
\end{aligned}
$
Where $r \leq n$ and $r \in W$
So, the number of ways arranging n different objects taken all at a time $=$ ${ }^n P_n=n!$
Types of Permutations
There are different types of permutations.
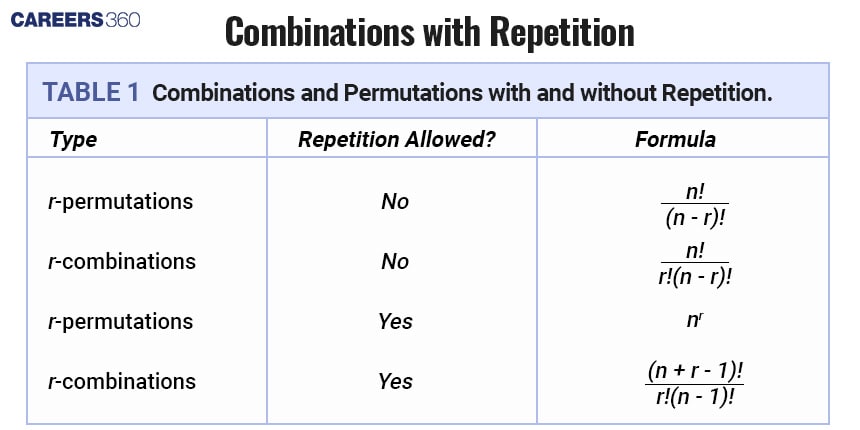
Permutation of $n$ different objects (when repetition is not allowed)
Repetition, where repetition is allowed
Permutation when the objects are not distinct (Permutation of multisets)
Permutation of $n$ different objects (when repetition is not allowed)
In this case, each object is used only once in the arrangement.
The formula to find the number of permutations of $n$ distinct objects is given by: $p(n) = n!$
Where $n!$ ($n$ factorial) is the product of all positive integers up to $n$
Permutation of $n$ different objects, where repetition is allowed
When repetition is allowed, each object can be used more than once in the arrangement. The formula to find the number of permutations when repetition is allowed is given by: $p(n,r) = nr$
Where $n$ is the total number of objects to choose from
And $r$ is the number of positions to be filled
Permutation when the objects are not distinct (Permutation of multisets)
When some objects are identical, the formula to find the number of distinct permutations is adjusted to account for the repetitions. The formula is given by:
$p(n: n_1, n_2, n_3,\ldots,......., n_k) = \frac{n!}{n_1! × n_2! × n_3! ×.........×n_k!}$
Where n is the number of total objects, $n_1, n_2, n_3,\ldots......., n_k$ are frequencies of different objects.
What is Circular Permutation?
When n objects are to be arranged circularly, then the formula to find the number of distinct permutations is given by (n-1)!.
What is the Combination?
A combination is a selection of items from a larger pool, where the order of the items does not matter. In other words, it is a way of selecting items where the arrangement or sequence of the selection is not considered.
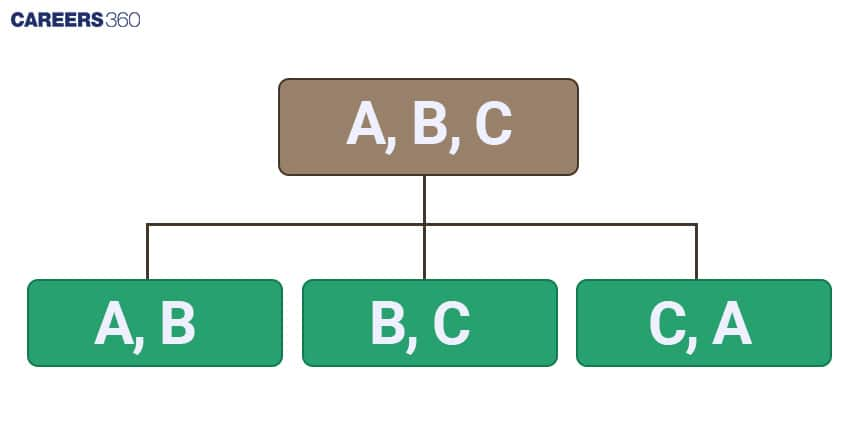
Suppose we want to select two objects from three distinct objects a, b and c. This can be stated as a number of combinations of four different objects taken two at a time.
Here we have three different combinations $ab, bc, ca, bc$. In other words, we can say that there are three ways in which we can select two objects from three distinct objects.
Combination Formula

We can generalize this concept for $r$ object to be selected from given $n$ objects as
$
\begin{aligned}
& { }^n C_r \times r!={ }^n P_r \\
& { }^n C_r=\frac{{ }^n P_r}{r!} \\
& { }^n C_r=\frac{n!}{(n-r)!r!}
\end{aligned}
$
Where $0 \leq r \leq n$, and $r$ is a whole number.
When is the Combination to be used?
Combinations are used when the order of selection does not matter. Here are some examples of when combinations are appropriate:
Lottery Selection Method: In the Lottery selection method, we use the combination method. Order does not matter in selecting lotteries to choose prize winners.
Forming Committees: When forming a committee from a group of people, the order in which members are chosen does not matter.
Choosing Subsets: When choosing a subset of items from a larger set, where the order in which items are chosen is irrelevant.
Hand of Cards: When selecting a hand of cards from a deck, the order of the cards in the hand does not matter.
Relation between Permutation and Combination
Theorem 1: $^np_r=^nc_r × r!$
Corresponding to each combination of $^nc_r$ we have $r!$ permutations because r objects in every combination can be rearranged in $r!$ ways.
Proof:
We have to prove that $^np_r=^nc_r × r!$
Taking the left side of the equation:
$^np_r=\frac{n!}{(n-r)!}$
Taking the right side of the equation
$^nc_r × r! = \frac{n!}{(n-r!) r!} × r! = \frac{n!}{(n-r)!}=^np_r$
Hence, $^np_r=^nc_r × r!$ proved.
Theorem 2: ${ }^n\mathrm{C}_r +{ }^n\mathrm{C}_{r-1} = { }^{n+1}\mathrm{C}_r$
Proof:
We have to prove that ${ }^n\mathrm{C}_r +{ }^n\mathrm{C}_{r-1} = { }^{n+1}\mathrm{C}_r$
Taking the left side of the equation, we get,
${ }^n\mathrm{C}_r +{ }^n\mathrm{C}_{r-1}$
= $\frac{n!}{r!(n-r)!}+\frac{n!}{(n-r+1)!(r-1)!}$
= $\frac{n!}{(n-r)!r(r-1)!}+\frac{n!}{(n-r+1)!(r-1)!}$
= $\frac{n!}{(r-1)!}[\frac{1}{(n-r)!r}+\frac{1}{(n-r+1)!}]$
= $\frac{n!}{(r-1)!}[\frac{1}{r(n-r)!}+\frac{1}{(n-r+1)(n-r)!}]$
= $\frac{n!}{(r-1)!(n-r)!}[\frac{1}{r}+\frac{1}{(n-r+1)}]$
= $\frac{n!}{(r-1)!(n-r)!}[\frac{n-r+1+r}{r(n-r+1)}]$
= $\frac{n!}{(r-1)!(n-r)!}[\frac{n+1}{r(n-r+1)}]$
= $\frac{(n+1)n!}{r(r-1)!(n-r+1)(n-r)!}$
= $\frac{(n+1)!}{r!(n-r+1)!}$
= ${ }^{n+1}\mathrm{C}_r$
Hence, proved.
Difference between Permutation and Combination
Permutation | Combination |
Permutation refers to the different possible arrangements of a given number of items taken some or all at a time. | A combination is a selection of items from a larger pool, where the order of the items does not matter. |
Order of arrangement is important. | Order of arrangement is not important. |
Permutations are for lists. | Combinations are for groups. |
The number of permutations of “$n$” objects taken “$r$” at a time is given by: $^n p_r =\frac{n!}{(n-r)!}$, Where $n$ = number of items $r$ = the number of items to be arranged | $^n c_r =\frac{n!}{r!(n-r)!}$, Where $n$ = number of items in a collection $r$ = the number of items from the collection to be chosen |
To remember:
Questions based on Permutation and Combination
1) 432
2) 108
3) 36
4) 18
Solution:
No. of 4 digits number formed $= 4!$
Now each digit comes equal no. of times at unit place $= 3!$
Each digit appears at the unit place
So sum $= 3! (3+4+5+6)$
$= 6 x 18 = 108$
Hence, the answer is the option 2.
1) 160
2) 120
3) 60
4) 48
Solution:
Odd numbers: $1, 1, 3$
Even numbers: $2, 2, 2, 4, 4$
Let us first find places for odd numbers.
$1, 1, 3$ can occupy any of the 4 even positions (2^\text{nd}, 4^\text{th}, 6^\text{th}, 8^\text{th}).
Choose 3 places for them: $\binom{4}{3} = 4$
Now, $1, 1, 3$ can be arranged in these 3 places in $\frac{3!}{2!} = 3$ ways.
Number of ways for placing odd numbers: $4 \times 3 = 12$
Now, $2, 2, 2, 4, 4$ can be arranged in the remaining 5 places.
Number of ways to arrange them: $\frac{5!}{3!2!} = 10$
So, total number of ways: $12 \times 10 = 120$
Hence, the answer is $120$.
1) 72
2) 60
3) 48
4) 36
Solution:
The sum of the given digits is $0 + 1 + 2 + 5 + 7 + 9 = 24$.
Let the 6-digit number be $abcdef$.
It is divisible by 11 if $|(a + c + e) - (b + d + f)|$ is a multiple of $11$.
Only one possible case: $a + c + e = b + d + f = 12$.
Case 1: $(a, c, e) = (7, 5, 0)$ and $(b, d, f) = (9, 2, 1)$
So, $2! \times 2! \times 3! = 2 \times 2 \times 6 = 24$ ways.
Case 2: $(a, c, e) = (9, 2, 1)$ and $(b, d, f) = (7, 5, 0)$
So, $3! \times 3! = 6 \times 6 = 36$ ways.
Total ways: $24 + 36 = 60$
Hence, the answer is $60$.
1) $10^5$
2) 9 × 8 × 7 × 6 × 5
3) 90,000
4) 95
Solution:
Method 1:
We have to fill $5$ slots.
The first digit can be any from $1$ to $9$ (not $0$), so $9$ options.
Each of the remaining $4$ slots can be filled by any digit from $0$ to $9$, so $10$ options for each.
Total numbers: $9 \times 10 \times 10 \times 10 \times 10 = 90000$
Method 2:
The total ways to choose any digit for $5$ places is $10^5$.
Out of these, $10^4$ numbers start with zero (if first digit is $0$, only $4$ slots left, each with $10$ choices).
So, the count of valid five-digit numbers is $10^5 - 10^4 = 90,!000$
Hence, the answer is $90000$.
1) 7
2) 15
3) 18
4) 22
Solution:
The number of ways of selecting South Indian food $15$.
The number of ways of selecting Japanese food is $7$.
Here a person may choose any one food item, either a South Indian or a Japanese food. So, we have to use "Addition" to find the total number of ways for selecting the food item.
The total number of selecting either a South Indian or Japanese food is $15+7=22$.
Hence, the answer is the option 4.
Crack JEE 2026 with JEE/NEET Online Preparation Program Start Now
List of topics related to Permutations and Combinations according to JEE MAIN/NCERT
Best Books and resources for Permutations and Combinations
Explore top recommended books designed to strengthen your understanding and problem-solving skills in permutations and combinations. These resources are ideal for exam preparation, offering clear explanations and practice questions to help you master this topic.
| Book Title | Author/Publisher | Description | Target Exam |
|---|---|---|---|
| Permutation and Combination: Book for Boards, NTSE, IIT JEE | Ramesh Chandra | Focused on serious exam preparation with in-depth coverage. | Boards, IIT JEE, NTSE |
| Combinatorial Theory | Marshall Hall Jr. | Advanced book covering deeper combinatorics and permutation theories. | Advanced undergraduates, graduates |
| NCERT Class 11 Mathematics Chapter 7 | NCERT | Official textbook covering fundamental theory and problems. | CBSE Students, Beginners |
| Permutations and Combinations Book | Arihant Publication | Helpful for practice and exam preparation. | Competitive Exam Aspirants |
NCERT Resources
NCERT resources offer simple and clear study materials for permutations and combinations. These resources help students understand key concepts easily and practice problems effectively for exams.
NCERT Maths Class 11 Notes for Chapter 7 - Permutations and Combinations
NCERT Maths Class 11 Solutions for Chapter 7 - Permutations and Combinations
NCERT Maths Class 11 Exemplar Solutions for Chapter 7 - Permutations and Combinations
NCERT Subjectwise Resources
NCERT subject-wise resources provide comprehensive and well-structured study materials across all major subjects. They offer easy access to textbooks, notes, solutions, making learning organized and effective for students at all academic levels.
| Resource Type | Mathematics | Physics | Chemistry | Biology |
|---|---|---|---|---|
| NCERT Notes | NCERT notes Class 11 Maths | NCERT notes Class 11 Physics | NCERT notes Class 11 Chemistry | NCERT notes Class 11 Biology |
| NCERT Solutions | NCERT solutions for Class 11 Mathematics | NCERT solutions for Class 11 Physics | NCERT solutions for Class 11 Chemistry | NCERT solutions for Class 11 Biology |
Practice Questions based on Permutations and Combinations
Practice questions on permutations and combinations are essential for mastering this topic. They help build problem-solving skills and improve speed and accuracy for exams.
Frequently Asked Questions (FAQs)
Permutation formula: $^nP_r = \frac{n!}{(n-r)!}$
Combination formula: $^nC_r = \frac{n!}{r!(n-r)!}$
Use permutation when order matters and combination when it doesn’t.
In permutation, $n$ represents the total number of items and $r$ represents the number of choosen items to be arranged.
Permutation is the arrangement of set of items in a specific order while combination is the selection of set of items.
A permutation is an arrangement in a definite order of a number of objects taken some or all at a time.
Combinations can be represented in terms of permutation. The formula for permutation is $P(n,r) = \frac{n!}{(n-r)!}$. The fomula for combinations is $C(n,r) = \frac{n!}{r!(n-r)!}$ which can be rewritten as $C(n,r) = \frac{P(n,r)}{r!}$
The formula for $nCr$ is $nCr = \frac{n!}{r!(n-r)!}$