Rolle’s Theorem: Definition, Formula, Examples, Questions

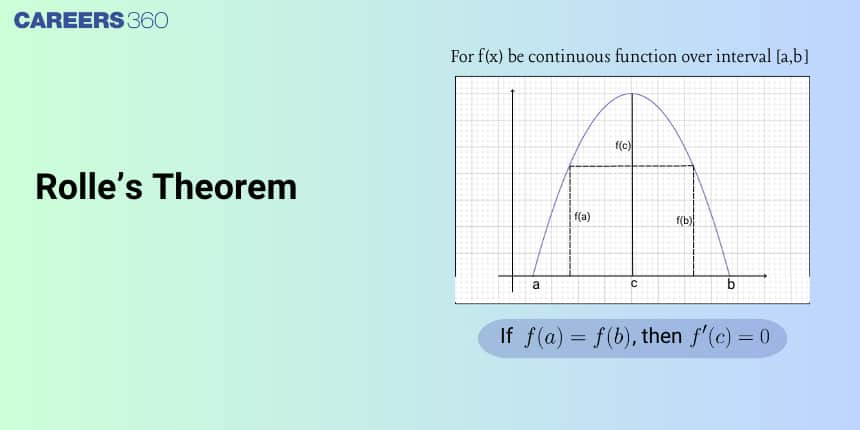
Definition of Rolle’s Theorem

Rolle’s Theorem is a fundamental concept in differential calculus that connects continuity, differentiability, and the existence of stationary points (points where the derivative equals zero). In simple words, it states that for a smooth curve starting and ending at the same height, there exists at least one point in between where the tangent to the curve is horizontal, i.e., its slope or derivative is zero.

This theorem forms the basis of the Mean Value Theorem (MVT) and is an essential tool in analyzing the behavior of differentiable functions within a given interval.

Mathematical Statement of Rolle’s Theorem

Let $f(x)$ be a real-valued function defined on the closed interval $[a, b]$. If the function satisfies the following conditions:

1. $f(x)$ is continuous on the closed interval $[a, b]$

2. $f(x)$ is differentiable on the open interval $(a, b)$

3. $f(a) = f(b)$

Then, there exists at least one point $c \in (a, b)$ such that

$ f'(c) = 0 $

This means that at $x = c$, the tangent to the curve $y = f(x)$ is parallel to the x-axis, indicating that the slope of the tangent line is zero.

Notations and Explanation of Each Term

• $f(x)$ → The given real-valued function defined on $[a, b]$

• $[a, b]$ → The closed interval over which the function is continuous

• $(a, b)$ → The open interval where the function is differentiable

• $f(a)$ and $f(b)$ → The function values at the endpoints of the interval, which are equal for Rolle’s Theorem to hold

• $f'(c)$ → The derivative (slope) of the function at the point $x = c$

• $c$ → The specific point in $(a, b)$ where $f'(c) = 0$

In essence, Rolle’s Theorem ensures that if a smooth function begins and ends at the same level, there must exist a point between them where the tangent is horizontal, i.e., the rate of change becomes zero. This point $c$ represents the location of a local extremum (maximum or minimum).

Geometrical interpretation of Rolle’s Theorem

Let $f(x)$ be a real-valued function defined on $[a,b]$ such that the curve $y=f(x)$ is continuous in $[a,b]$ and it is possible to draw a unique tangent at every point on the curve $y=f(x)$ between points $A$ and $B$. Also, the ordinates at the endpoints of the interval $[a,b]$ are equal. Then there exists at least one point $(c,f(c))$ lying between $A$ and $B$ on the curve $y=f(x)$ where the tangent is parallel to the x-axis. i.e. $f′(c)=0$.

If the function is continuous and differentiable and if $f(x)=0$ has two roots $\alpha$ and $\beta$, then from Rolle's theorem there exists at least one root of the equation $f′(x)=0$ in the interval $(\alpha,\beta)$. Similarly, for a twice differentiable function $y=f(x)$, between any two roots of the equation $f′(x)=0$, there exists at least one root of the equation $f′′(x)=0$ and so on.

Note:
The converse of Rolle’s theorem need not be true.

For example,
Let $f(x)=x^3−x^2−x+1$ in the interval $[−1,2]$
$f′(x)=3x^2−2x−1$
$f′(1)=3(1)^2−2(1)−1=0$ but $f(−1)≠f(2)$

Applications of Rolle’s Theorem

Rolle’s Theorem plays a crucial role in mathematical analysis and calculus, especially when it comes to understanding the behavior of differentiable functions and locating roots of equations. It provides a bridge between the existence of roots and the slope of the tangent to the curve, making it a powerful tool in both pure mathematics and engineering applications.

Importance of Rolle’s Theorem

Rolle’s Theorem is used to:

• Identify intervals where the derivative of a function equals zero.

• Prove the existence of stationary points in a function.

• Establish the mean value theorem as its generalization.

• Find the roots of equations and determine where they lie on a given interval.

• Analyze the increasing and decreasing behavior of continuous functions.

Using Rolle’s Theorem to Locate Roots

Let’s explore a simple example to understand how the theorem works in practice.

Consider the function
$f(x) = (x - 1)(x - 2)(x - 3)(x - 4)$

We are asked to find how many positive roots the equation $f'(x) = 0$ has.

Since $f(x)$ is a polynomial function, it is continuous and differentiable everywhere on $\mathbb{R}$.
Also,
$f(1) = f(2) = f(3) = f(4) = 0$

According to Rolle’s Theorem, for every pair of consecutive zeros of $f(x)$, there exists at least one value of $x$ in between where the derivative $f'(x) = 0$.

Thus, there must be at least one root of $f'(x) = 0$ in each of the intervals:
$(1, 2)$, $(2, 3)$, and $(3, 4)$

Since $f'(x)$ is a cubic polynomial, it can have at most three real roots.
Therefore, there is exactly one root of $f'(x) = 0$ in each of these intervals.

Hence, all three roots are positive.

The number of positive roots of $f'(x) = 0$ is 3.

Proof of Rolle's Theorem

consider the portion AB of the curve y=f(x), lying between x=a and x=b, such that

Conditions for Rolle’s Theorem (Graphical View)

For a function $f(x)$ defined on $[a, b]$, the following three conditions must hold true:

1. It goes continuously from point A to point B, i.e., $f(x)$ is continuous on $[a, b]$.

2. It has a tangent at every point between $A$ and $B$, implying that $f(x)$ is differentiable on $(a, b)$.

3. The ordinate of A equals the ordinate of B, i.e., $f(a) = f(b)$.

These ensure the function forms a smooth and closed curve between $A$ and $B$ without any breaks or corners.

Graphical Behavior of the Function

From the figure (conceptually), the curve $y = f(x)$:

• Increases in the interval $AC_1$, indicating that $f'(x) > 0$ in this region.

• Decreases in the interval $C_1B$, indicating that $f'(x) < 0$ in this region.

Since the function is continuous and differentiable between points $A$ and $B$, and each tangent has a unique slope (unique value of $f'(x)$), there must exist at least one point between $A$ and $B$ where the slope of the tangent line is zero.

Existence of Stationary Point

By the Mean Value Theorem of Derivatives, and due to the smooth transition from positive to negative slope, there exists at least one point $x = c$ such that

$f'(c) = 0$, where $a < c < b$.

At this point, the tangent to the curve is horizontal and parallel to the x-axis.

Hence, under the given conditions of continuity, differentiability, and equal ordinates at endpoints, the function $f(x)$ satisfies the condition of Rolle’s Theorem.

Thus, it is proven that there exists at least one point $c \in (a, b)$ such that $f'(c) = 0$ — meaning the tangent at $(c, f(c))$ is parallel to the x-axis.

Lagrange’s Mean Value Theorem (LMVT)

The Lagrange’s Mean Value Theorem (LMVT) is a key concept in Class 12 that builds upon Rolle’s Theorem. It connects the average rate of change of a function over an interval to its instantaneous rate of change at a specific point within that interval. Essentially, LMVT states that for a smooth and continuous curve, there exists at least one point where the tangent line is parallel to the secant line joining the interval’s endpoints.

Statement of Lagrange’s Mean Value Theorem

Let $f(x)$ be a real-valued function defined on the closed interval $[a, b]$ such that:

1. $f(x)$ is continuous on $[a, b]$

2. $f(x)$ is differentiable on $(a, b)$

Then there exists at least one real number $c \in (a, b)$ such that

$f'(c) = \frac{f(b) - f(a)}{b - a}$

This expression shows that there is some point $x = c$ within the interval where the derivative of the function (instantaneous rate of change) equals the average rate of change between $a$ and $b$.

Geometrical Interpretation of LMVT

Geometrically, the Lagrange’s Mean Value Theorem means that if $f(x)$ is continuous on $[a, b]$ and differentiable on $(a, b)$, then there exists a point $c \in (a, b)$ such that the tangent at $(c, f(c))$ is parallel to the secant line joining $(a, f(a))$ and $(b, f(b))$.

In simple terms:

• The slope of the secant line between the points $(a, f(a))$ and $(b, f(b))$ is given by $\frac{f(b) - f(a)}{b - a}$.

• The slope of the tangent line at $x = c$ is given by $f'(c)$.

• According to LMVT, these two slopes are equal, i.e., $f'(c) = \frac{f(b) - f(a)}{b - a}$.

Relation Between LMVT and Rolle’s Theorem

The Lagrange’s Mean Value Theorem generalizes Rolle’s Theorem.

• In Rolle’s Theorem, the function satisfies $f(a) = f(b)$, so the secant line is horizontal and $f'(c) = 0$ for some $c \in (a, b)$.

• In LMVT, this condition is removed — the secant line can have any slope. The theorem guarantees that there exists at least one point $c$ where the tangent is parallel to the secant, i.e., $f'(c) = \frac{f(b) - f(a)}{b - a}$.

Importance of Lagrange’s Mean Value Theorem

The LMVT is widely used in calculus and real analysis to:

• Determine the rate of change of a function between two points.

• Prove function inequalities and continuity-related results.

• Derive advanced results such as the Cauchy Mean Value Theorem and Taylor’s Theorem.

• Analyze the behavior of differentiable functions and understand how their derivatives influence shape and growth.

Solved Examples Based On Rolle's Theorem

Example 1:Let $f$ and $g$ be twice differentiable even functions on $(-2,2)$ such that $f\left(\frac{1}{4}\right)=0$, $f\left(\frac{1}{2}\right)=0$, $f(1)=1$ and $g\left(\frac{3}{4}\right)=0$, $g(1)=2$. Then, the minimum number of solutions of $f(x)g''(x) + f'(x)g'(x) = 0$ in $(-2,2)$ is equal to: [JEE Main 2022]

1. $4$

2. $3$

3. $1$

4. $6$

Solution:
Let $h(x) = f(x) \cdot g'(x)$.

So $h(x)$ is continuous and differentiable.

Now as $f\left(\frac{1}{4}\right) = f\left(\frac{1}{2}\right) = 0$ and $f(x)$ is an even function, so $f\left(-\frac{1}{4}\right) = f\left(-\frac{1}{2}\right) = 0$ which means

$h\left(-\frac{1}{2}\right) = h\left(-\frac{1}{4}\right) = h\left(\frac{1}{4}\right) = h\left(\frac{1}{2}\right) = 0$

So $-\frac{1}{2}, -\frac{1}{4}, \frac{1}{4}, \frac{1}{2}$ are 4 roots of $h(x)$

Also $g'(0) = 0$ ($g(x)$ is even differentiable function) $\Rightarrow h(0) = 0$

From minimum roots of $h(x)$, $g(x)$ may look something like this:

$\therefore \ h(x)$ has minimum $5$ roots: $-\frac{1}{2}, -\frac{1}{4}, 0, \frac{1}{4}, \frac{1}{2}$

So, $h'(x) = f' g' + f g''$ has at least $4$ roots

Hence, answer is $4$

Example 2: Let $f: \to \mathbb{R}$ be a twice differentiable function in $(0,1)$ such that $f(0) = 3$ and $f(1) = 5$. If the line $y = 2x + 3$ intersects the graph of $f$ at only two distinct points in $(0,1)$, then the least number of points $x \in (0,1)$ at which $f''(x) = 0$, is _________________ [JEE Main 2022]
1) 2
2) 1
3) 7
4) 4

Solution

f′(a)=f′(b)=f′(c)=2
⇒f′′(x) is zero
for at least x1∈(a,b)&x2∈(b,c)

Hence, two number of points.

Example 3: If $c$ is a point at which Rolle's theorem holds for the function $f(x)=\log_e(x^2+\alpha 7x)$ in the interval $$, where $\alpha\in\mathbb{R}$, then $f''(c)$ is equal to: [JEE Main 2020]

1. $-\frac{1}{24}$

2. $-\frac{1}{12}$

3. $3^7$

4. $\frac{1}{12}$

Solution:
$f(3)=f(4)\ \Rightarrow\ 9+\alpha 3=16+\alpha 4$
$\alpha=12$
$f'(x)=\frac{x^2-12x}{x^2+12}$
$f'(c)=0\ \Rightarrow\ c=12$
$f''(c)=\frac{1}{12}$
Hence, the answer is the option $(4)$.

Example 4: Let $f:(a,b)\to\mathbb{R}$ be a twice differentiable function such that $f(x)=\int_a^x g(t)dt$ for a differentiable function $g(x)$. If $f(x)=0$ has exactly five distinct roots in $(a,b)$, then $g(x)g'(x)=0$ has at least: [JEE Main 2021]

1. Twelve roots in $(a,b)$

2. Five roots in $(a,b)$

3. Seven roots in $(a,b)$

4. Three roots in $(a,b)$

Solution:
$f(x)=\int_a^x g(t)dt$
Differentiating:
$f'(x)=g(x) \cdot 1 - g(a) \cdot 0$
$f'(x)=g(x)\ \Rightarrow\ f''(x)=g'(x)$

Now $f(x)$ has $5$ roots in $(a,b)$

$\Rightarrow f'(x) \ (=g(x)) $ has at least $4$ roots in $(a,b)$ and $g'(x)$ has at least $3$ roots in $(a,b)$
So $g(x)\cdot g'(x)$ has at least $7$ roots in $(a,b)$.

Hence, the answer is the option $(3)$.

Example 5: Let $f$ be any continuous function on $$ and twice differentiable on $(0,2)$. If $f(0)=0$, $f(1)=1$ and $f(2)=2$, then: [JEE Main 2021]

1. $f''(x)>0$ for all $x\in(0,2)$

2. $f'(x)=0$ for some $x\in$

3. $f''(x)=0$ for some $x\in(0,2)$

4. $f''(x)=0$ for all $x\in(0,2)$

Solution:
Let $g(x)=f(x)-x$
$g(0)=0$, $g(1)=0$, $g(2)=0$
Apply Rolle's Theorem for $g(x)$ in There exist a $C_1\in(0,1)$ s.t. $g'(C_1)=0\ \Rightarrow\ f'(C_1)-1=0\ \Rightarrow\ f'(C_1)=1$ Rolle's theorem in for $g(x)$
There exist a $C_2\in(1,2)$ s.t.
$g'(C_2)=0\ \Rightarrow\ f'(C_2)-1=0\ \Rightarrow\ f'(C_2)=1$

Rolle's theorem in $[C_1, C_2]$ for $f'(x)$
$\Rightarrow$ There exist a $C \in (C_1, C_2) \subset (0,2)$, s.t.
$f''(C)=0$
Hence, the answer is the option $(3)$.

List of topics related to Rolle’s Theorem

This section gives a complete overview of all essential subtopics connected to Rolle’s Theorem, including differentiability, continuity of composite functions, and existence of derivatives. Understanding these topics helps build a strong foundation for applying Rolle’s Theorem and analyzing function behavior between given intervals.

Differentiability and Existence of Derivative

Examining differentiability Using Graph of Function

Continuity of Composite Function

Continuity And Differentiability

NCERT Resources

This section compiles the most reliable NCERT Class 12 Mathematics materials for Chapter 5 – Continuity and Differentiability. These resources include notes, solved examples, and exemplar solutions to help you understand and apply Rolle’s Theorem with clarity.

NCERT Class 12 Maths Notes for Chapter 5 - Continuity and Differentiability

NCERT Class 12 Maths Solutions for Chapter 5 - Continuity and Differentiability

NCERT Class 12 Maths Exemplar Solutions for Chapter 5 - Continuity and Differentiability

Practice Questions based on Rolle’s Theorem:

This section provides MCQs and practice problems designed to test your grasp of Rolle’s Theorem and its application in verifying the existence of stationary points. Practicing these questions will help you gain confidence in identifying where $f'(x) = 0$ within an interval.

Rolles Theorem- Practice Question MCQ

We have shared below the links to practice questions on the related topics to Rolle’s Theorem: