Maxima and Minima - Definition, Types, Graph, Examples

Maxima and Minima of a Function

A function is a special type of relation where every element of one set corresponds to exactly one element of another set.
Formally, if $A$ and $B$ are two non-empty sets, then a relation from $A$ to $B$ is called a function if each element $x \in A$ is assigned a unique element $f(x) \in B$.

It is denoted as:
$f: A \rightarrow B$,
and read as “$f$ is a mapping from $A$ to $B$.”

In calculus, the study of maxima and minima of a function helps determine where a function reaches its highest (maximum) or lowest (minimum) values within an interval.

Critical Points and Extrema

Let $f$ be a continuous function defined on an open interval $I$. A point $c \in I$ is called a critical point of $f$ if either $f'(c) = 0$ or $f'(c)$ does not exist.
At these points, the function may attain a local maximum or local minimum depending on the behavior of its derivative.

First Derivative Test for Maxima and Minima

Case (i): Local Maximum

If the derivative $f'(x)$ changes sign from positive to negative as $x$ increases through $c$, that is:

• $f'(x) > 0$ at every point sufficiently close to and to the left of $c$, and

• $f'(x) < 0$ at every point sufficiently close to and to the right of $c$,

then $x = c$ is a point of local maximum.
In this case, the function increases before $c$ and decreases after $c$, creating a peak on the graph.

Case (ii): Local Minimum

If the derivative $f'(x)$ changes sign from negative to positive as $x$ increases through $c$, that is:

• $f'(x) < 0$ at every point sufficiently close to and to the left of $c$, and

• $f'(x) > 0$ at every point sufficiently close to and to the right of $c$,

then $x = c$ is a point of local minimum.
Here, the function decreases before $c$ and increases after $c$, forming a trough on the graph.

Graphical Interpretation

In the graph of $y = f(x)$:

• A local maximum appears as the highest point of a curve within a neighborhood.

• A local minimum appears as the lowest point in a neighborhood.

The first derivative $f'(x)$ indicates the slope of the tangent at each point.
At maxima or minima, the tangent is horizontal, i.e., $f'(x) = 0$.

Point to be noted: The first derivative test is one of the most effective methods for determining the increasing and decreasing behavior of a function, helping to identify local extrema.

Definition of Maximum and Minimum Values of a Function

Let $y = f(x)$ be a real-valued function defined at $x = a$.

The function $f(x)$ is said to have a maximum value at $x = a$ if
$f(x) \leq f(a)$ for all $x \in \mathbb{R}$ in the neighborhood of $a$.

Similarly, the function $f(x)$ is said to have a minimum value at $x = a$ if
$f(x) \geq f(a)$ for all $x \in \mathbb{R}$ in the neighborhood of $a$.

Concept of Local Maxima and Local Minima

A function $f(x)$ is said to have a local maximum (or local maxima) at a point $x = a$ if the value of the function at $a$ is greater than the values of $f(x)$ for all $x$ in a small neighborhood around $a$.

In simpler terms, $f(x)$ has a maximum at $x = a$ if $f(a + h) \leq f(a)$ and $f(a - h) \leq f(a)$, where $h > 0$ is a very small positive quantity.

Similarly, $f(x)$ has a local minimum at $x = a$ if $f(a + h) \geq f(a)$ and $f(a - h) \geq f(a)$ for all small $h > 0$.

A function $f(x)$ is said to have a local minimum (or local minima) at a point $x = b$ if the value of the function at $b$ is less than the values of $f(x)$ for all $x$ in a small neighborhood around $b$.

In other words, $f(x)$ has a minimum at $x = b$ if
$f(b + h) \geq f(b)$ and $f(b - h) \geq f(b)$, where $h > 0$ is a very small positive quantity.

Methods to find points of Local maxima and Local minima

Condition for Local Maxima and Minima Using Derivatives

At the points of local maxima and minima, the slope of the tangent drawn to the curve becomes zero.

• For local maximum, $\dfrac{dy}{dx}$ changes from positive to negative.

• For local minimum, $\dfrac{dy}{dx}$ changes from negative to positive.

Mathematical Representation

Let $y = f(x)$, then
$\dfrac{dy}{dx} = f'(x)$

At points where the function attains extrema (maximum or minimum),
$f'(x) = 0$

Second Derivative Test

To determine the nature of stationary points using the second derivative test, follow these steps:

Step 1: Find the values of $x$ for which $\dfrac{dy}{dx} = 0$.

Step 2:
If $x = x_0$ is such that

• $f''(x_0) < 0$, then $x_0$ is a point of local maximum.

• $f''(x_0) > 0$, then $x_0$ is a point of local minimum.

Solved Examples Based on Maxima and Minima of a Function:

Example 1: Let the tangents drawn to the circle, $x^2+y^2=16$ from the point P(0, h) meet the x-axis at points A and B. If the area of $\Delta APB$ is minimum, then h is equal to : [JEE Main 2015]

1) $4\sqrt{3}$

2) $3\sqrt{3}$

3) $3\sqrt{2}$

4) $4\sqrt{2}$

Solution:

Maxima Minima -

A functions graph follows up and down along the x-axis then the upper part is known as maxima and lower part is known as minima.

-

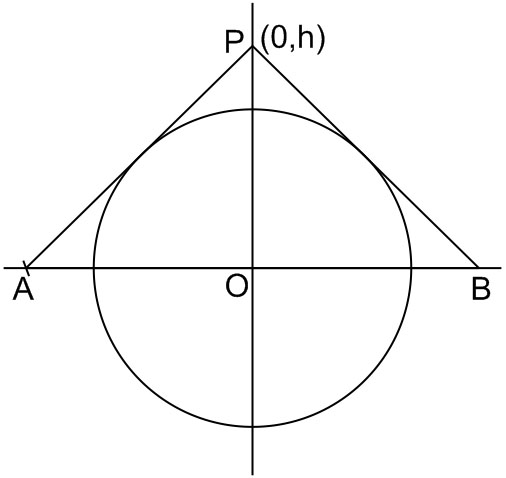
Let equation of tangent is

$(y-h)=M(x-0)$

$\therefore y=Mx-h$

$\therefore h=\pm\sqrt{1+M^{2}}$

$\therefore AB=\pm\frac{4\sqrt{1+M^{2}}}{M}$

$\therefore Area =\frac{1}{2}\times AB\times OP$

$=\frac{1}{2}\times \frac{8\sqrt{1+M^{2}}}{M}\times 4\sqrt{1+M^{2}}$

$\frac{dA}{dm}=0$ $\therefore m = 1$

$\therefore h=4\sqrt{1+1}$$=4\sqrt{2}$

Example 2: If $f(x)$ is non-zero polynomial of degree four,having local extreme points at $x=-1,0,1;$ then the set $S=\left \{ x\; \epsilon\; R:f(x)=f(0) \right \}$ contains exactly : [JEE Main 2019]

1) four irrational numbers.

2) four rational numbers.

3) two irrational and two rational numbers.

4) two irrational and one rational number.

Solution:

Given that

$f\left ( x \right )=f\left ( 0 \right )$

$a\left ( \frac{x^{4}}{4}-\frac{x^{2}}{2} \right )+c=c$

$\left ( \frac{x^{4}}{4}-\frac{x^{2}}{2} \right )=0$

$\Rightarrow x^{2}\left ( x^{2}-2 \right )=0$

$x=0,\pm \sqrt{2}$

$S=\left \{ 0,\sqrt{2},-\sqrt{2} \right \}$

Example 3: The maximum volume (in cu.m) of the right circular cone having a slant height 3 m is: [JEE Main 2019]

1) $6\pi$

2) $3\sqrt{3}\pi$

3) $\frac{4}{3}\pi$

4) $2\sqrt3\pi$

Solution:

Method for maxima or minima

By second derivative method:

Step 1. Find values of x for $\frac{dy}{dx} = 0$

Step 2. $x = x_{0}$ is a point of local maximum if $f''(x) < 0$ and local minimum if $f''(x) > 0$

Where $y = f(x)$

and $\frac{dy}{dx} = f'(x)$

$l = 3m$ (slant height)

$h = 3\cos(\theta)$

$r = 3\sin(\theta)$

Volume of right circular cone

$V = \frac{1}{3}\pi r^{2}h$

$= \frac{1}{3}\pi (3\sin(\theta))^{2}(3\cos(\theta))$

$V = \frac{\pi}{3} \times 9\sin^{2}\theta \times 3\cos(\theta) = 9\pi\sin^{2}\theta\cos(\theta)$

for maximum volume

$\frac{dv}{d\theta} = 0,;; \frac{dv}{d\theta} = -9\pi\sin(\theta)[\sin^{2}(\theta) - 2\cos^{2}(\theta)] = 0$

$\sin(\theta) = \sqrt{\frac{2}{3}}$

$\frac{d^{2}v}{d\theta^{2}} = -ve; at; \sin(\theta) = \sqrt{\frac{2}{3}}$

Volume is maximum when $\sin(\theta) = \sqrt{\frac{2}{3}}$

$\therefore V_{max} = 2\sqrt{3}\pi$ (cu.m)

Example 4: If p(x) is a polynomial of degree three that has a local maximum value 8 at x=1 and a local minimum value 4 at x=2; then p(0) is equal to: [JEE Main 2020]

1) 6

2) -12

3) -24

4) 12

Solution:

Since $p(x)$ has relative extreme at $x = 1$ and $x = 2$,

so $p'(x) = 0$ at $x = 1$ and $x = 2$

$\Rightarrow p'(x) = A(x - 1)(x - 2)$

$\Rightarrow p(x) = \int A(x^2 - 3x + 2),dx$

$p(x) = A\left(\frac{x^3}{3} - \frac{3x^2}{2} + 2x\right) + C \ldots(1)$

Now, $p(1) = 8$

From (1):

$8 = A\left(\frac{1}{3} - \frac{3}{2} + 2\right) + C$

$\Rightarrow 8 = \frac{5A}{6} + C$

$\Rightarrow 48 = 5A + 6C$

Also, $p(2) = 4$

$\Rightarrow 4 = A\left(\frac{8}{3} - 6 + 4\right) + C$

$\Rightarrow 4 = \frac{2A}{3} + C$

$\Rightarrow 12 = 2A + 3C$

From above, solving:

$48 = 5A + 6C$
$12 = 2A + 3C$

$\Rightarrow A = 24,; C = -12$

Therefore, $p(0) = C = -12$

Example 5: If a rectangle is inscribed in an equilateral triangle of side length $2 \sqrt{2}$ as shown in the figure, then the square of the largest area of such a rectangle is__________. [JEE Main 2021]

1) 3

2) 1

3) 4

4) 6

Solution:

Let height of rectangle $= x$

$\frac{x}{y} = \tan 60^{\circ} \Rightarrow y = \frac{x}{\sqrt{3}}$

$\therefore \text{Length of rectangle} = 2\sqrt{2} - 2y = 2\sqrt{2} - \frac{2x}{\sqrt{3}}$

$\text{Area of rectangle} = x \left( 2\sqrt{2} - \frac{2x}{\sqrt{3}} \right)$

$= 2\sqrt{2}x - \frac{2}{\sqrt{3}}x^{2}$

For maximum area, $\Rightarrow 2\sqrt{2} - \frac{4}{\sqrt{3}}x = 0 , , \left(f'(x) = 0\right)$

$\Rightarrow x = \sqrt{\frac{3}{2}}$

$\text{Area} = 2\sqrt{2} \cdot \sqrt{\frac{3}{2}} - \frac{2}{\sqrt{3}} \cdot \frac{3}{2} = 2\sqrt{3} - \sqrt{3} = \sqrt{3}$

$\text{Square of Area} = 3$

List of topics related to Maxima and Minima

This section lists the essential subtopics connected to Maxima and Minima, helping students understand key calculus concepts like continuity, differentiability, and critical points that determine local and global extrema.

Differentiability and Existence of Derivative

Examining differentiability Using Graph of Function

Continuity of Composite Function

Continuity And Differentiability

NCERT Resources

This section compiles important NCERT Class 12 Maths study materials for Chapter 5, guiding students through reliable notes, textbook exercises, and exemplar problems related to continuity, differentiability, and applications like Maxima and Minima.

NCERT Class 12 Maths Notes for Chapter 5 - Continuity and Differentiability

NCERT Class 12 Maths Solutions for Chapter 5 - Continuity and Differentiability

NCERT Class 12 Maths Exemplar Solutions for Chapter 5 - Continuity and Differentiability

Practice Questions based on Maxima and Minima

Practice conceptual and application-based MCQs on Maxima and Minima to test your understanding and improve accuracy for board exams and entrance-level assessments.

Maxima And Minima In Calculus- Practice Question MCQ

We have shared below the links to practice questions on the related topics to Maxima and Minima: