Set Theoretical Notations of Probability

Set theoretical notations provide a clear way to represent events and their relationship These operations on the events show us how the values are related to each other. Fundamental operations are union, intersection, and complement. These operations can help analysts to predict the likelihood of an event.

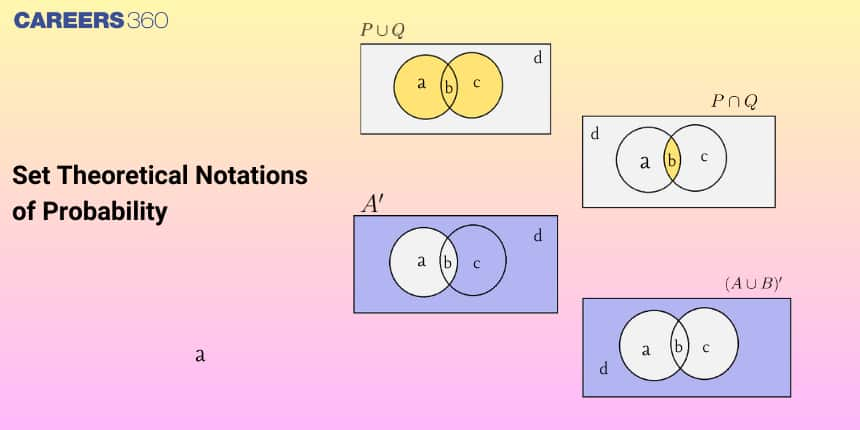
Set Theoretical Notations of Probability

A set is simply a collection of distinct objects, considered as a whole. These objects, called elements or members of the set, can be anything: numbers, people, letters, etc. Sets are particularly useful in defining and working with groups of objects that share common properties.

An experiment is called a random experiment.

1. A possible result of a random experiment is called its outcome and the set of all possible outcomes of a random experiment is called Sample Space. Generally, sample space is denoted by $S$.

2. The set of outcomes from an experiment is known as an Event.

3. Two or more than two events are said to be mutually exclusive if the occurrence of one of the events excludes the occurrence of the other.

4. If an event has only one sample point of a sample space, it is called a simple (or elementary) event.

Sets Operations:

1. Union: The union of $A$ and $B$ is the set that consists of all the elements of A and all the elements of B, the common elements being taken only once. The symbol $'∪’$ is used to denote the union. Symbolically, we write $A U B = \{x: x ∈ A or x ∈ B\}.$

2. Intersection: The intersection of sets A and B is the set of all elements that are common to both A and B. The symbol $'∩'$ is used to denote the intersection. Symbolically, we write $A ∩ B = \{x: x ∈ A and x ∈ B\}$

3. Difference: The difference of the sets $A$ and $B$ in this order is the set of elements that belong to $A$ but not to $B$. Symbolically, we write $A – B$ and read as “$A$ minus $B$”.

4. Complement: Let $U$ be the universal set and $A$ is a subset of $U$. Then the complement of $A4$ is the set of all elements of U which are not the elements of $A$. Symbolically, we use A' or A^c to denote the complement of $A$ with respect to $U$. $A' = \{x∶ x ∈ U$ and $x ∉ A \}$. Obviously, $A' = U – A$

5. Cartesian Product: The Cartesian product of two sets $A$ and $B$, denoted by $A×B$ is the set of all ordered pairs $(a,b)$ where $a$ is an element of $A$ and $b$ is an element of $B$.

The Addition Rule of Probability

(Probability of the event $'A$ or $B'$ )

If $A$ and $B$ are any two events defined on a sample space, then the probability of occurrence of at least one of the events $A$ and $B$ is $P(A ∪ B)$ and it equals $P(A) + P(B) - P(A ∩ B)$.

From the set theory, we know that

$
\mathrm{n}(\mathrm{A} \cup \mathrm{B})=\mathrm{n}(\mathrm{A})+\mathrm{n}(\mathrm{B})-\mathrm{n}(\mathrm{A} \cap \mathrm{B})
$

Divide by $n(S)$ both side

$
\begin{aligned}
& \frac{n(A \cup B)}{n(S)}=\frac{n(A)}{n(S)}+\frac{n(B)}{n(S)}-\frac{n(A \cap B)}{n(S)} \\
& P(A \cup B)=P(A)+P(B)-P(A \cap B)
\end{aligned}
$

Special case

If $A$ and $B$ are disjoint sets, i.e., they are mutually exclusive events, then $A ∩ B = φ.$ Therefore $P(A ∩ B) = P (φ) = 0$

Thus, for mutually exclusive events $A$ and $B$, we have $P(A ∪ B) = P(A) + P(B), $

If $A$ and $B$ are two events, then

$ (A - B) ∩ (A ∩ B) = φ$ and $ A = (A - B) ∪ (A ∩ B) $

So, $ P(A) = P(A - B) + P(A ∩ B) - 0$

$= P(A ∩ B’) + P(A ∩ B) $

or $P(A) - P(A ∩ B) = P(A ∩ B’) = P(A - B)$ $[∵ A - B = A ∩ B’ ]$

Similarly, $P(B) - P(A ∩ B) = P(B ∩ A’) = P(B - A) $

If $A, B$ and $C$ are any three events in a sample space $S$, then

$P(A ∪ B ∪ C) = P(A) + P(B) + P(C) - P(A ∩ B) - P(A ∩ C) - P(B ∩ C) + P(A ∩ B ∩ C)$

If $A, B$ and $C$ are any three mutually exclusive events in a sample space $S$, then

$P(A ∪ B ∪ C) = P(A) + P(B) + P(C)$

Probability of event ‘not A’ or Complementary Event

If $E$ is the any event and $E’$ be the complement of the event $E$. Since, $E$ and $E’$ are disjoint and exhaustive sets.

$\begin{array}{ll} & \mathrm{E} \cup \mathrm{E}^{\prime}=S \\ \therefore & \mathrm{n}\left(\mathrm{E} \cup \mathrm{E}^{\prime}\right)=\mathrm{n}(\mathrm{S}) \\ \Rightarrow & \mathrm{n}(\mathrm{E})+\mathrm{n}\left(\mathrm{E}^{\prime}\right)=\mathrm{n}(\mathrm{S}) \\ \Rightarrow \quad & \frac{\mathrm{n}(\mathrm{E})}{\mathrm{n}(\mathrm{S})}+\frac{\mathrm{n}\left(\mathrm{E}^{\prime}\right)}{\mathrm{n}(\mathrm{S})}=1 \\ \Rightarrow \quad & \mathrm{P}(\mathrm{E})+\mathrm{P}\left(\mathrm{E}^{\prime}\right)=1 \\ \text { or } & \mathrm{P}(\mathrm{E})=1-\mathrm{P}(\text { not } \mathrm{E})=1-\mathrm{P}\left(\mathrm{E}^{\prime}\right)\end{array}$

Recommended Video Based on Set Theoretical Notations

Solved Examples Based on Set Theoretical Notations:

Example 1: Two dice are thrown. What is the probability that the sum of the numbers on the two dice is eight?

1) $\frac{5}{36}$
2) $\frac{5}{18}$
3) $\frac{1}{4}$
4) $\frac{1}{3}$

Solution

Favourable Cases

$
\begin{aligned}
& =\{(6,2),(2,6),(5,3),(3,5),(4,4) \\
& =5
\end{aligned}
$
Total Cases
$
\begin{aligned}
=36=\{ & (1,1),(1,2),(1,3) \\
& (2,1),(2,2), \ldots(6,6)\}
\end{aligned}
$
So, required probability

$
=\frac{5}{36}
$

Hence, the answer is the option(1).

Example 2: In a class of $200$ students, $125$ students have taken a programming language course, $85$ students have taken a data structures course, $65$ students have taken a computer organization course, $50$ students have taken both programming languages and data: structures, $35$ students have taken both programming languages and computing organization, $30$ students have taken both data structures and computer organization, $15$ students have taken all the three courses. How many students have not taken any of the three courses?

1) $15$

2) $20$

3) $25$

4) $35$

Solution

Method I :

Using Venn diagram we can easily see that Number of students have not taken any of the three subjects $=25$

Method II :

Let $\mathrm{p}=$ programming language, $\mathrm{D}=$ Data structure, $\& \mathrm{C}=$ computer organization

Given

$
\begin{aligned}
& \mathrm{p}(\mathrm{P})=\frac{125}{200}, \mathrm{p}(\mathrm{D})=\frac{85}{200}, \mathrm{p}(\mathrm{C})=\frac{65}{200} \\
& \mathrm{p}(\mathrm{P} \cap \mathrm{D})=\frac{50}{200}, \mathrm{p}(\mathrm{P} \cap \mathrm{C})=\frac{35}{200} \\
& \mathrm{p}(\mathrm{D} \cap \mathrm{C})=\frac{30}{200}, \mathrm{p}(\mathrm{P} \cap \mathrm{D} \cap \mathrm{C})=\frac{15}{200}
\end{aligned}
$

Using Addition theorem,

$
\begin{aligned}
\mathrm{p}(\mathrm{P} \cup \mathrm{D} \cup \mathrm{C}) & =p(\mathrm{P})+\mathrm{p}(\mathrm{D})+\mathrm{p}(\mathrm{C})-\mathrm{p}(\mathrm{P} \cap \mathrm{D}) \\
- & \mathrm{p}(\mathrm{D} \cap \mathrm{C})-\mathrm{p}(\mathrm{P} \cap \mathrm{C})+\mathrm{p}(\mathrm{P} \cap \mathrm{D} \cap \mathrm{C}) \\
& =\frac{7}{8} \\
\Rightarrow \mathrm{P}(\overline{\mathrm{P}} \cap \overline{\mathrm{D}} \cap \overline{\mathrm{C}})= & 1-\mathrm{P}(\mathrm{P} \cup \mathrm{D} \cup \mathrm{C})
\end{aligned}
$

$
=1-\frac{7}{8}=\frac{1}{8}
$

Hence, Number of students who had not taken any of the three courses

$
=\frac{1}{8} \times 200=25
$

Example 3: Two coins are simultaneously tossed. The probability of two heads simultaneously appearing
1) $\frac{1}{8}$
2) $\frac{1}{6}$
3) $\frac{1}{4}$
4) $\frac{1}{2}$

Solution

Set of possible outcomes

$
\begin{aligned}
& \qquad=\{(\mathrm{HH}),(\mathrm{HT}),(\mathrm{TH}),(\mathrm{TT})\} \\
& \text { Set of favorable outcomes }=\{(\mathrm{HH})\} \\
& \therefore \text { The required probability }=\frac{1}{4}
\end{aligned}
$

Hence, the answer is the option (3).
Example 4:
A fair coin is tossed independently four times. the probability of the event "the number of times heads show up is more than the number of times tails show up is
1) $\frac{1}{16}$
2) $\frac{1}{8}$
3) $\frac{1}{4}$
4) $\frac{5}{16}$

Solution
$
\mathrm{n}(\mathrm{s})=16
$

Favorable cases $=\{ HHHT, HHTH, HTHH, THHH, HHHH \}$
No of favorable cases $=5$
Required Probability $=\frac{5}{16}$
Hence, the answer is the option (4).

Example 5: The probability that a given positive integer lying between 1 and 100 (both inclusive) is NOT divisible by $2$, $3$ , or $5$ is
1) $0.26$
2) $0.36$
3) $0.21$
4) $0.23$

Solution

Number of integers in the set which are divisible by

$
\begin{aligned}
& 2 \text { or } 3 \text { or } 5= \\
& \begin{aligned}
\mathrm{n}(2 \cup 3 \cup 5)= & \mathrm{n}(2)+\mathrm{n}(3)+\mathrm{n}(5)-\mathrm{n}(2 \cap 3) \\
& -\mathrm{n}(3 \cap 5)-\mathrm{n}(5 \cap 2)+\mathrm{n}(2 \cap 3 \cap 5) \\
& =50+33+20-16-10-6+3 \\
& =74
\end{aligned}
\end{aligned}
$

$\therefore$ The number of integers between 1 and 100 which are not divisible by 2 or 3 or $5=n(\overline{2} \cap \overline{3} \cap \overline{5})$

$
\begin{aligned}
& \text { The number of integers between } 1 \text { and } 100 \text { which are not divisible by } 2 \text { or } 3 \text { or } 5=\mathrm{n}(\overline{2} \cap \overline{3} \cap \overline{5}) \\
& \qquad=100-74 \\
& =26
\end{aligned}
$

$\therefore$ Req. probability

$
=\frac{26}{100}=0.26
$