Centre Of Mass Of Semicircular Disc

The concept of the centre of mass is pivotal in understanding the balance and stability of objects in various fields of science and engineering. When examining a semicircular disc, which is essentially half of a full circular disc, the centre of mass plays a crucial role in determining its equilibrium and behaviour under different forces. In real life, this concept is not just an abstract idea but has practical implications. For example, in designing rotating machinery or even in the architecture of curved bridges, knowing the precise centre of mass helps to ensure stability and efficiency. The semicircular disc provides a fascinating study in balancing and dynamics, shedding light on how partial shapes distribute their mass and interact with external forces, thus bridging theoretical physics with tangible real-world applications

This Story also Contains

1. Definition of Centre of Mass
2. Centre of Mass of a Continuous Distribution
3. Solved Examples Based on the Centre of Mass of the Semicircular Disc
4. Summary

Definition of Centre of Mass

The Centre of mass of a body is defined as a single point at which the whole mass of the body or system is imagined to be concentrated and all external forces are applied there. It is the point where if a force is applied it moves in the direction of the force without rotating.

Centre of Mass of a Continuous Distribution

The centre of mass of a continuous distribution is a key concept in physics that extends beyond simple, discrete systems to more complex, continuous ones. Unlike objects with distinct masses located at specific points, continuous distributions involve mass spread over a region, such as a rod, a plate, or even a fluid. To find the centre of mass in such cases, we consider each infinitesimally small mass element and calculate its contribution to the overall position.

$x_{c m}=\frac{\int x d m}{\int d m}, y_{c m}=\frac{\int y d m}{\int d m}, z_{c m}=\frac{\int z d m}{\int d m}$

Where dm is the mass of the small element. x, y, z are the coordinates of the dm part.

The Centre of Mass of the Semicircular Disc

Have a look at the figure of the semicircular disc

Since it is symmetrical about the y-axis on both sides of the origin

So, we can say that its $x_{c m}=0$
And it's $z_{c m}=0$ as the z-coordinate is zero for all particles of the semicircular ring.
Now we will calculate its $Y_{\mathrm{cm}}$ which is given by

$
y_{c m}=\frac{\int y \cdot d m}{\int d m}
$

So, Take a small elemental ring of mass dm of radius x on the disc.

$
d m=\frac{2 M}{\pi R^2} \pi x(d x)
$
As we know semicircular ring $y_{c m}=\frac{2 R}{\pi}$
So, for the elemental ring $y$-the coordinate is $y_{\mathrm{cm}}=\frac{2 x}{\pi}$
So, $y_{c m}=\frac{1}{M} \int_0^R\left(\frac{2 x}{\pi} d m\right)$

$
\begin{aligned}
& y_{c m}=\frac{1}{M} \int_0^R\left(\frac{4 M}{\pi R^2} x^2 d x\right) \\
& y_{c m}=\frac{4 R}{3 \pi}
\end{aligned}
$

Recommended Topic Video

Solved Examples Based on the Centre of Mass of the Semicircular Disc

Example 1: A rigid ball of mass m strikes a rigid, wall at $60^{\circ}$ and gets reflected without loss of speed as shown in the figure below. The value of impulse imparted by the wall on the ball will be

1) mV
2) 2 mV
3) $\frac{m V}{2}$
4) $\frac{m V}{3}$

Solution

Law of Conservation of Momentum

$\begin{aligned} & \vec{F}=\frac{\overrightarrow{d p}}{d t} \\ & \vec{F}=0 \quad \text { then } \vec{p}=\text { constant } \\ & \vec{p}=\vec{p}_1+\vec{p}_2+\cdots=\text { const }\end{aligned}$

wherein

Independent of frame of reference

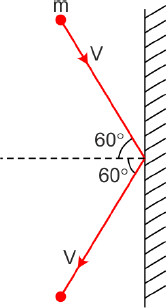
After doing components,

$\begin{aligned} & V_1=V \frac{1}{2} \hat{i}-V \frac{\sqrt{3}}{2} \hat{j} \\ & V_2=-V \frac{1}{2} \hat{i}-V \frac{\sqrt{3}}{2} \hat{j} \\ & \text { Impulse }=m V_1-m V_2=m V\end{aligned}$

Hence, the answer is the option (1).

Example 2: A long solenoid of diameter 0.1 m has 2 x 10⁴ turns per meter. At the centre of the solenoid, a coil of 100 turns and a radius of 0.01 m is placed with its axis coinciding with the solenoid axis. The current in the solenoid reduces at a constant rate to 0 A from 4 A in 0.05 s. If the resistance of the coil is $10 \pi^2 \Omega$, the total charge flowing through the coil during this time is:

1) $32 \pi \mu \mathrm{C}$
2) $16 \mu \mathrm{C}$
3) $32 \mu \mathrm{C}$
4) $16 \pi \mu \mathrm{C}$

Solution:

The field at the centre of the solenoid $B=\mu_0 N_l i$
where NI -number of turns per unit length
Flux through the inner loop $=100 \times \pi 0.01^2 B=100 \times \pi 0.01^2 \times \mu_0 N_l i$
emf induced $=$ rate of change of flux $=\frac{\Delta \phi}{\Delta t}=100 \times \pi 0.01^2 \times \mu_0 N_l \frac{\Delta i}{\Delta t}$

Current through loop $=$

$
i=\frac{e m f}{R}=\frac{\Delta \phi}{\Delta t}=100 \times \pi 0.01^2 \times \mu_0 N_l \frac{\Delta i}{\Delta t} \frac{1}{R}
$
Total charge through the coil during this time

$
i \Delta t=\frac{\Delta \phi}{\Delta t}=100 \times \pi 0.01^2 \times \mu_0 N_l \Delta i \frac{1}{R}=3.2 \times 10^{-5} C
$

Hence, the answer is the option (3).

Summary

The centre of mass is a fundamental concept in physics, crucial for understanding the balance and stability of objects like a semicircular disc. For a semicircular disc, the centre of mass is located along the axis of symmetry and can be determined using calculus. For continuous distributions, the centre of mass is calculated by integrating the mass elements' positions. Practical examples, such as the impact of forces on objects and induced currents in coils, illustrate the application of these principles in real-world scenarios, highlighting their importance in engineering and physics.