• Engineering and Architecture
  • Management and Business Administration
  • Medicine and Allied Sciences
  • Law
  • Animation and Design
  • Media, Mass Communication and Journalism
  • Finance & Accounts
  • Computer Application and IT
  • Pharmacy
  • Hospitality and Tourism
  • Competition
  • School
  • Study Abroad
  • Arts, Commerce & Sciences
  • Learn
  • Online Courses and Certifications
Distance Time Graph

Distance Time Graph

Vishal kumarUpdated on 02 Jul 2025, 05:03 PM IST

A distance-time graph represents how distance changes with time, an easy way to visualize motion. Imagine keeping track of your daily commute: as you pass by time, you are at various distances from home. A distance-time graph can describe whether you are going at a constant speed, slowing down, or stopping at signals. It is a powerful tool in physics, which deals with the issues of motion analysis and interpretation, and thus helpful to understand how speed, distance, and time are interrelated for all sorts of common life situations from driving to cycling to walking. In this article, we are going to learn about distance-time graphs, distance-time graphs for uniform motion, non-uniform motion and body at rest and many more.

Distance Time Graph
Distance Time Graph

What is a Distance-Time Graph?

A distance-time graph is a graph that shows the way in which the distance covered by an object varies with time. Time is represented along the x-axis while distance is along the y-axis. The shape and steepness of the line on a distance-time graph permits a determinate of the speed of an object when at constant speed, acceleration or if it is at rest. For instance, a straight positive sloping line indicates constant speed and a horizontal flat line would mean that the object is static. Graphs of distance over time are able to better image and understand motion patterns in physical settings and many other real-life situations.

Importance of Distance-Time Graph

When examining the motion of bodies, we use the distance-time graph. A distance-time graph relating to the motion of a body can be obtained by recording distance and time for the motion of a body and plotting the same data on a rectangle graph.

Also read :

NEET Highest Scoring Chapters & Topics
This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.
Download E-book

Types of Distance-Time Graph

There are two types of motion uniform and non-uniform motion

Uniform Motion:

The motion of an item in which the object moves along a straight line and its velocity remains constant along that line while it covers equal distances in equal intervals of time, regardless of the length of time, is referred to as this sort of motion.

The above diagram represents the distance-time graph for uniform motion

Example of Uniform Motion:

  • When an automobile travels at a speed of 10 m/s, it travels 10 metres in one second.
  • Every second, the speed remains constant.
  • The blades of a ceiling fan move back and forth.

Non Uniform Motion:

The motion of an object in which the object travels at a variable speed and does not cover the same distance in equal time intervals, regardless of the time interval duration, is referred to as this sort of motion.

The above diagram shows the Distance vs time graph for non-uniform motion

Example of Non-Uniform Motion:

  • If a car travels 10 metres in the first two seconds and 15 metres in the next two seconds, the total distance travelled is 15 metres.
  • Body at rest:

When a body or object is at rest, then the distance-time graph can be represented as follows:

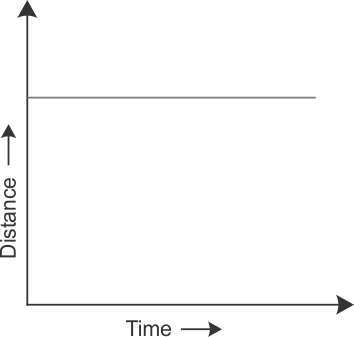
Distance time graph for body at rest

The above diagram shows a distance-time graph for a body at rest

Related Topics

What are the Uses of the Distance-Time Graph


1. The character of motion is seen at a glance.

2. Relative motion at different intervals is possible.

3. Without performing any calculations, the zone of acceleration or retardation can be calculated.

4. The distance of a moving body can be computed at any time unit.

Frequently Asked Questions (FAQs)

Q: What does a distance-time graph look like for an object experiencing a sudden impact?
A:
A sudden impact would appear as an abrupt change in the graph's direction or slope. There might be a sharp corner where the impact occurs, followed by a different slope representing the post-impact motion. The exact shape would depend on the nature of the impact and the object's subsequent motion.
Q: How do you represent the motion of a pendulum on a distance-time graph?
A:
A pendulum's motion would be represented by a sinusoidal curve on a distance-time graph. The distance would oscillate smoothly between maximum positive and negative values, with the amplitude possibly decreasing over time due to air resistance.
Q: How do you represent the motion of an elevator on a distance-time graph?
A:
An elevator's motion could be represented by alternating sloped and horizontal lines. Upward slopes show ascent, downward slopes show descent, and horizontal lines represent stops at different floors.
Q: What does the distance-time graph of a car's journey look like if it encounters traffic?
A:
A car encountering traffic might have a distance-time graph with alternating steep and shallow slopes, or even horizontal segments. Steep slopes represent periods of normal driving, shallow slopes indicate slow traffic, and horizontal lines show complete stops.
Q: How can you use a distance-time graph to determine if an object ever comes to a complete stop?
A:
An object comes to a complete stop when its distance remains constant for a period of time. This would appear as a horizontal line segment on the distance-time graph.
Q: What does a distance-time graph look like for an object moving with simple harmonic motion?
A:
Simple harmonic motion, like that of an ideal spring, would be represented by a sinusoidal curve on a distance-time graph. The distance oscillates smoothly between maximum positive and negative values.
Q: How do you represent the motion of an object on a frictionless surface on a distance-time graph?
A:
An object on a frictionless surface with an initial push would be represented by a straight line on a distance-time graph. The object would continue at constant velocity (assuming no other forces), resulting in a constant slope.
Q: How do you represent the motion of a bouncing ball on a distance-time graph?
A:
A bouncing ball would be represented by a series of parabolic curves. Each bounce would show as an upward curve (ball rising) followed by a downward curve (ball falling). The peaks of these curves would decrease over time due to energy loss.
Q: What does a distance-time graph look like for an object moving in a circle at constant speed?
A:
For an object moving in a circle at constant speed, the distance-time graph would be a straight line with positive slope. Although the object is changing direction, its distance from the starting point is continuously increasing at a constant rate.
Q: How can you use a distance-time graph to determine when two moving objects meet?
A:
If the distance-time graphs for two objects are plotted on the same axes, the point where these graphs intersect represents the time and position where the objects meet.
Articles