Relative Speed in Opposite Direction.

The object or body relative speed in a distinct direction is shown: Let us say a man is traveling from Ajmer to Delhi, and the second man is traveling from Delhi to Ajmer in opposite directions. Then we can find out the relative speed as (a+b) or the sum of two velocities.

A train of length 200m traveling at a speed of 30m/s over takes second one having 300 m train length that is traveling at a pace of 20ms −1in the similar direction. The time taken by the 1st train to pass the second train is:

If we see in question, then both two trains are moving in same direction, Therefore the relative speed = 30-20 = 10m/s Total distance = 200 + 300 = 500m Therefore, the time taken = 500 / 10 =50s

2nd sitting in train means?

2nd refers to second seating or second seater in train seats. The seats are present within the sort of benches. This coach doesn't have the power for the passengers to sleep since there are not any berths and it's a sitting arrangement.

What is the opposite of fast and opposite of moving?

Opposite of fast-Slow Opposite of moving- Stationary

How does relative speed differ from absolute speed?

Relative speed considers the motion of two objects in relation to each other, while absolute speed refers to an object's speed relative to a fixed point or frame of reference. In reality, all motion is relative, and absolute speed is a theoretical concept.

Why is understanding relative speed important in physics?

Understanding relative speed is crucial because it helps explain how motion appears different from various perspectives. It's fundamental to many physics concepts, including Einstein's theory of relativity, and has practical applications in navigation, sports, and transportation.

Can relative speed be negative?

Yes, relative speed can be negative. This occurs when two objects are moving towards each other. The sign (positive or negative) indicates the direction of motion relative to the chosen frame of reference.

How do you calculate relative speed when two objects are moving in the same direction?

When two objects are moving in the same direction, their relative speed is the difference between their individual speeds. If object A is moving at 50 km/h and object B at 30 km/h in the same direction, their relative speed is 50 - 30 = 20 km/h.

What happens to relative speed when objects move in opposite directions?

When objects move in opposite directions, their relative speed is the sum of their individual speeds. For example, if two cars approach each other at 60 km/h and 40 km/h respectively, their relative speed is 60 + 40 = 100 km/h.

How does the concept of relative speed apply to everyday situations?

Relative speed is experienced in many everyday situations, such as passing cars on a highway, walking on a moving walkway in an airport, or a passenger moving inside a moving train. In each case, the speed experienced depends on the chosen frame of reference.

What is the formula for relative speed?

The general formula for relative speed is: v_relative = v_1 - v_2, where v_1 is the velocity of the first object and v_2 is the velocity of the second object. The sign of the result indicates the direction of relative motion.

How does relative speed relate to the concept of frame of reference?

Relative speed is intrinsically linked to the frame of reference. The same motion can appear different depending on the chosen reference point. For instance, a passenger walking in a moving train has different speeds relative to the train and to the ground outside.

Can two objects have zero relative speed?

Yes, two objects can have zero relative speed if they are moving at the same velocity (speed and direction) relative to a given frame of reference. For example, two cars traveling side by side at the same speed on a highway have zero relative speed to each other.

How does relative speed affect the Doppler effect?

Relative speed is crucial in the Doppler effect. As a source of waves (like sound or light) and an observer move relative to each other, the perceived frequency of the waves changes. This is why a passing siren sounds different as it approaches and moves away.

What role does relative speed play in collision physics?

In collision physics, relative speed is essential for determining the outcome of collisions. The relative speed between colliding objects affects the energy transfer and the resulting velocities after the collision, regardless of their individual speeds before impact.

How is relative speed used in navigation?

In navigation, relative speed is used to calculate the time and fuel needed for journeys, especially when dealing with moving air or water currents. For instance, a plane's ground speed (relative to Earth) differs from its airspeed (relative to the air) due to wind.

Can relative speed exceed the speed of light?

No, relative speed cannot exceed the speed of light according to Einstein's theory of special relativity. The speed of light is the universal speed limit, and no information or matter can travel faster relative to any frame of reference.

How does relative speed affect time dilation in special relativity?

In special relativity, high relative speeds between objects lead to time dilation. As the relative speed between two frames of reference approaches the speed of light, time appears to slow down for the fast-moving object from the perspective of the slower frame.

What is the difference between relative speed and relative velocity?

Relative speed is a scalar quantity that only considers the magnitude of relative motion, while relative velocity is a vector quantity that includes both magnitude and direction. Relative velocity provides more complete information about the relative motion.

How do you solve relative speed problems involving rivers or currents?

In problems involving rivers or currents, you need to consider the speed of the object relative to the water and the speed of the water relative to the ground. The actual speed and direction of the object relative to the ground is the vector sum of these two velocities.

What is the significance of relative speed in sports?

In sports, relative speed is crucial for strategy and performance. For example, in tennis, the relative speed between the ball and the racket affects the power and direction of the shot. In team sports, players must constantly adjust their movements based on the relative speeds of teammates and opponents.

How does relative speed affect energy calculations in physics?

Relative speed is important in energy calculations because kinetic energy depends on speed squared. In collisions or interactions between objects, it's the relative speed that determines the energy transfer, not their individual speeds in an arbitrary frame of reference.

Can relative speed help explain the twin paradox in relativity?

Yes, relative speed is key to understanding the twin paradox. The twin who travels at high speed relative to Earth experiences time dilation, aging less than the Earth-bound twin. This apparent paradox is resolved by considering the acceleration and deceleration of the traveling twin, which breaks the symmetry between the two reference frames.

How does air resistance affect relative speed calculations?

Air resistance can significantly affect relative speed calculations, especially at high speeds. It introduces a velocity-dependent force that opposes motion, causing objects to have different relative speeds in air compared to a vacuum. This is particularly important in aerodynamics and ballistics.

What is the relationship between relative speed and closing speed?

Closing speed is a specific application of relative speed. It refers to the rate at which two objects approach each other. For objects moving directly towards each other, the closing speed is the sum of their individual speeds. It's crucial in collision avoidance systems and space navigation.

How does relative speed apply to orbital mechanics?

In orbital mechanics, relative speed is essential for calculating orbital transfers, rendezvous maneuvers, and gravitational assists. The relative speed between a spacecraft and a celestial body determines the shape of the orbit and the energy required for various maneuvers.

Can relative speed be used to explain the aberration of light?

Yes, the aberration of light is a phenomenon directly related to relative speed. It occurs due to the relative motion between the Earth and distant light sources, causing stars to appear in slightly different positions than they actually are. This effect was crucial in proving Earth's motion around the Sun.

How does relative speed affect the perception of time in everyday life?

While not noticeable in everyday life due to the low speeds involved, relative speed does theoretically affect the perception of time. This becomes significant only at very high speeds, as described by special relativity, where time dilation becomes measurable.

What is the importance of relative speed in GPS technology?

Relative speed is crucial in GPS technology. The system must account for the relative motion between satellites and receivers, as well as relativistic effects due to the satellites' high orbital speeds and Earth's gravity, to provide accurate positioning information.

How does relative speed relate to the concept of simultaneity in physics?

Relative speed challenges the concept of absolute simultaneity in physics. According to special relativity, events that appear simultaneous in one frame of reference may not be simultaneous in another frame moving at a high relative speed. This leads to the relativity of simultaneity.

Can relative speed explain why we don't feel Earth's rotation?

Yes, relative speed explains why we don't feel Earth's rotation. Our everyday experiences are based on motion relative to Earth's surface. Since we rotate with the Earth, our relative speed to the ground is zero, making the rotation imperceptible in our daily lives.

How is relative speed used in designing transportation systems?

Relative speed is a key consideration in designing transportation systems. It's used to calculate safe distances between vehicles, determine optimal speeds for fuel efficiency, and design systems for collision avoidance. It's particularly important in air traffic control and autonomous vehicle technology.

What role does relative speed play in understanding the expansion of the universe?

Relative speed is fundamental to understanding the expansion of the universe. The observed redshift of distant galaxies is interpreted as a relative speed of recession, leading to the conclusion that the universe is expanding. This forms the basis of the Hubble-Lemaître law in cosmology.

What is the significance of relative speed in understanding the behavior of subatomic particles?

In particle physics, relative speed is crucial for understanding particle interactions and decay processes. The lifetimes of unstable particles can appear to change due to time dilation at high relative speeds, affecting their observed behavior in particle accelerators and cosmic rays.

How does relative speed relate to the concept of proper time in relativity?

Proper time is the time measured by a clock traveling with an object. As relative speed increases, the proper time experienced by the moving object slows down compared to a stationary observer's time. This relationship is key to understanding time dilation in special relativity.

Can relative speed explain the phenomenon of length contraction?

Yes, relative speed is directly related to length contraction. According to special relativity, objects moving at high relative speeds appear shortened in the direction of motion when observed from a stationary frame. This effect becomes significant as speeds approach that of light.

How does relative speed affect the calculation of momentum in collisions?

In collision physics, it's the relative speed between objects that determines the exchange of momentum. The total momentum of a closed system is conserved, but how it's distributed after a collision depends on the relative speeds of the colliding objects before and after the impact.

What is the relationship between relative speed and the concept of spacetime in physics?

Relative speed is intrinsically linked to the concept of spacetime. In special relativity, high relative speeds cause distortions in both space and time, leading to effects like time dilation and length contraction. These effects can be visualized and calculated using spacetime diagrams.

How does relative speed influence the design of particle accelerators?

Relative speed is a crucial factor in particle accelerator design. Accelerators aim to achieve very high relative speeds between particles to study high-energy collisions. The design must account for relativistic effects and the energy required to accelerate particles to near-light speeds.

What role does relative speed play in understanding the behavior of light in different media?

Relative speed is crucial in understanding light's behavior in different media. The speed of light in a medium is always relative to that medium. This leads to phenomena like refraction, where light changes direction when entering a new medium due to the change in its relative speed.

How does relative speed relate to the concept of relativistic velocity addition?

Relativistic velocity addition deals with combining velocities in situations where relative speeds are very high. Unlike in classical physics, velocities don't simply add linearly at relativistic speeds. The formula for relativistic velocity addition ensures that the combined speed never exceeds the speed of light.

Can relative speed explain why muons from cosmic rays reach Earth's surface?

Yes, relative speed explains this phenomenon. Muons produced in the upper atmosphere should decay before reaching Earth's surface. However, due to their high relative speed to Earth, they experience significant time dilation. This slows their decay in Earth's frame of reference, allowing them to reach the surface.

Relative Speed - Definition, Formula, FAQs

Q: What is relative speed?

Relative speed is the velocity at which one object appears to move in relation to another object. It takes into account the motion of both objects and depends on the frame of reference chosen for observation.

Vishal kumarUpdated on 02 Jul 2025, 05:03 PM IST

In this article, we will discuss, what is meant by relative? What is the meaning of speed? What is relative speed? What is relative speed formula?/ How to calculate relative speed? What is example of relative speed? How can we check the train speed? So let’s see.
Note: stationary meaning in tamil is நிலையான, relatives meaning in telugu is బంధువులు

Relative Speed

What is meant by relative?

“Relative” means “in comparison to”. The relative meaning in Tamil is உறவினர் (Uravinar), the Relative meaning in Telugu is చుట్టపువాడు. The stationary meaning in telugu is నిశ్చలమైన (Niscalamaina). Thus, the conceptualization of relative speed is used when two or more bodies in motion with some pace (speed) are contemplated. To make things easier, one body are often made stationary (i.e. Speed = 0) and take the pace of the other body with respect to the stationary body, which is the sum of the speeds if the bodies are moving in the converse i.e., opposite direction and the distinction if relative speed moving in the same direction. This speed of the moving body with reference to the stationary body is known as the relative Speed.

Relative speed of 2 bodies = Sum of their individual pace (speeds) if they are moving in the opposite direction = Distinction of their individual pace if they are moving in the same direction.

Also read -

What is the meaning of speed?

Speed is the ratio of distance travelled by unit time. It is a scalar quantity as it has only magnitude.

Expression for speed of a body travelling in a straight line is given by:

r= d / t

Here r is the speed, d is the distance covered, t is the time.

How to calculate relative speed?

Formula for relative speed: Assume two bodies are moving at a different pace (speed) in the same direction.

Consider the speed of first body occur x km/hr

And the speed of the second body occurs y km/hr .

Therefore, its relative speed is = (x-y)km/hr [x>y]

Next,

The time after which both the bodies meet = distance travelled / relative speed

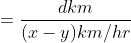
$=\frac{dkm}{(x-y)km/hr}$

Therefore, we already know that relative speed is the speed of one object with reference to another.

So, time after which each of two bodies meet,

Assume, time = t hrs.

So, the distance covered in ‘t’ hours = relative speed × time

= (x – y) km/hr × t hrs.

Related Topics Link,

What is train?

A train may be a kind of rail transport consisting of a series of connected vehicles that generally line a railroad (or railway) track to move passengers or cargo (also referred to as "freight" or "goods").

What is move/define move.

Definition of move: In physics, move/motion is the occurrence in which a body or object changes its position over time. Motion is mathematically found in terms of displacement, distance, velocity, acceleration, speed, and time. As there is no absolute frame of reference, absolute motion cannot be found.

What is train speed formula?

The train speed check can be done using the train Speed Formula.

Here are a few problems on trains for easy and prompt solutions of train-based questions:

Remember some pivotal formulas of train problems for quick solutions.

xkm/hr=x×5 / 18(m/s)
x m/s=x×18 / 5(km/hr)
Time taken by the object (train) of length L to travel a pole or a single post or a standing man is equal to the time taken by the train to cover L distance.
Time taken by the train of length l meters (m) to move an unmoving object of length b meters is the time taken by train to cover (l + b) meters.
Assume that bodies or two trains are travel (moving) in the same direction at

μm/s & v m/s

Where u>v then the relative speed in the same direction is

= (u - v) m/s.

Assume that two objects/bodies or two trains are moving in the opposite direction at u m/s andv m/s, then their relative's speed is = (u + v) m/s.
Let us consider that the two trains of length A,B are moving in opposite direction at u m/s & v m/s, then interval taken by the trains to intersect or cross each other is = (A+B)/(u+v)
Let us consider two trains of length A meters (m) and B meters (m) getting in a same direction at u m /s & v m/ s,

Then the time taken by the faster train to intersect the slower train

= (A+B)/(u-v)

Consider two bodies trains starting at same time from points A and B in the direction (way) of each other and after crossing they take a and b sec in reaching B and A respectively, then

(A’s speed): (B's speed) =(b:a).

Also Read:

What is an example of relative speed?

1. Two trains running in opposite directions cross a man standing on the station in 27 s (Seconds) and 17 s respectively and they intersect (cross) each other in 23 seconds. The ratio of their speed is ____?

Solution:

Let the speeds of the two trains be x m/sec and y m/sec .

So, length of the 1st train = 27x m (metres)

And length of the 2nd train = 17y m (metres).

∴ 27x+17y / x+y=23

Therefore: 27x+17y=23x+23y

4x=6y

So, x / y=3 / 2

Therefore, the ratio of their speeds is 3:2

A body is moving with velocity 30 m/s towards east/a body is moving with velocity 30m s towards east. After 10 s its velocity becomes 40 m/s towards north. The average acceleration of the body is

Solution: We have to formula used

$\vec{a}=\frac{\vec v-\vec u}{t}$

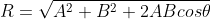
$R=\sqrt{A^2+B^2+2AB cos\theta}$

Acceleration is the change in velocity in one unit of your time. It tells us the speed at which the speed of a given body is increasing or decreasing with reference to time. In other words, what proportion of the speed is increasing or decreasing in one unit time.

Average acceleration is defined because of the difference within the final and initial velocities of the body upon the time taken by the body to succeed in the ultimate velocity from its initial velocity.

i.e. a=v-u / t……..(1)

Where a = acceleration of the body,

v = initial velocity and u = final velocity respectively and

t = time taken by the body.

Since, velocity and acceleration are vector quantities. Therefore we can write the Eq.(i) is,

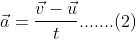
$\vec a=\frac{\vec v-\vec u}{t}.......(2)$

To determine the average acceleration (a) of the given body, first determine the value of v, u and t.

Initial velocity is

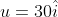
$u=30\hat{i}$

Final velocity is

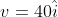
$v=40\hat{i}$

Change in the velocity

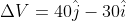
$\Delta V=40\hat{j}-30\hat{i}$

Magnitude is

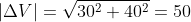
$\left |\Delta V \right |=\sqrt{30^2+40^2}=50$

Average acceleration is

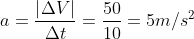
$a=\frac{\left | \Delta V \right |}{\Delta t}=\frac{50}{10}=5m/s^2$

Also check-

NCERT Physics Notes:

Frequently Asked Questions (FAQs)

Q: Can relative speed explain the phenomenon of gravitational time dilation?

While gravitational time dilation is primarily a consequence of general relativity, it can be related to relative speed. In the equivalence principle, the effects of gravity can be equated to acceleration. This leads to time dilation effects similar to those caused by high relative speeds in special relativity.

Q: How does relative speed affect the concept of mass-energy equivalence (E=mc²)?

While E=mc² holds in all reference frames, relative speed affects how energy and mass are perceived. At high relative speeds, kinetic energy contributes significantly to an object's total energy, leading to an apparent increase in mass from the perspective of a stationary observer.

Q: What role does relative speed play in understanding the behavior of neutrinos?

Relative speed is crucial in studying neutrinos. These particles travel at speeds very close to light speed, exhibiting extreme relativistic effects. Their high relative speed to Earth allows scientists to study phenomena like neutrino oscillations and test the limits of special relativity.

Q: How does relative speed relate to the concept of proper length in relativity?

Proper length is the length of an object measured in its rest frame. As relative speed increases between an object and an observer, the object appears shorter to the observer due to length contraction. The proper length remains constant, but the observed length depends on the relative speed.

Q: Can relative speed help explain the concept of relativistic Doppler effect?

Yes, relative speed is fundamental to the relativistic Doppler effect. Unlike the classical Doppler effect, the relativistic version accounts for time dilation at high speeds. This leads to different frequency shifts for light sources moving at high relative speeds, crucial in astrophysics and cosmology.

Q: How does relative speed influence the design of space missions?

Relative speed is a critical factor in space mission design. It affects trajectory calculations, fuel requirements, and mission duration. Engineers must consider the relative speeds of spacecraft, planets, and other celestial bodies to plan efficient routes and maneuvers, including gravity assists.

Q: What is the significance of relative speed in understanding the twin paradox?

Relative speed is key to resolving the twin paradox. While both twins see the other moving away at high speed, only the traveling twin experiences acceleration and deceleration, breaking the symmetry. This leads to real time dilation for the traveling twin, who ages less than the Earth-bound twin.

Q: How does relative speed affect the concept of causality in physics?

Relative speed is crucial to maintaining causality in physics. The universal speed limit (speed of light) ensures that cause always precedes effect in all reference frames, preserving the order of events. This prevents paradoxes that could arise if information could travel faster than light.

Q: How does relative speed affect the calculation of kinetic energy in different reference frames?

The calculation of kinetic energy depends on the chosen reference frame and thus on relative speed. While the total energy of a system is conserved, the distribution between kinetic and potential energy can vary depending on the relative motion of the observer. This is particularly important in relativistic energy calculations.

Q: How does relative speed affect the concept of simultaneity in different reference frames?

Relative speed directly impacts simultaneity in different reference frames. Events that appear simultaneous to one observer may not be simultaneous to another moving at a different speed. This counterintuitive result of special relativity challenges our everyday notions of time and space.

Articles

DU LLB Fee Structure 2026 - Check Complete Details

Sep 11, 2025

Top 5 Career Options after B.Arch - Eligibility, Salary Trends

Sep 11, 2025

Top 6 Career Options after BAF - Eligibility, Salary

Sep 06, 2025

Gujarat Paramedical Merit List 2025 Revised (Out): Download PDF Rank List

Sep 04, 2025