Drift Velocity - Meaning, Formula, FAQs

Edited By Team Careers360 | Updated on Jul 02, 2025 04:28 PM IST

The free electrons in a conductor are always in a continuous random motion due to the thermal energy of the conductor and the average speed at which free electrons 'drift' in the presence of an electric field is called drift velocity. In this article, we will discuss what is drift velocity, the drift velocity formula, the relation between current density and drift velocity, the relation between drift velocity and electric current, and factors affecting drift velocity. Over the last ten years of the JEE Main exam (from 2013 to 2023), nine questions have been asked on this concept.

This Story also Contains

What is Drift Velocity Class 12?
Drift Velocity Formula Class 12
Relation Between Current Density and Drift Velocity
Relation Between Drift Velocity and Electric Current
Factors Affecting Drift Velocity
Important Terms Related to Drift Velocity
Solved Examples Based on Drift Velocity

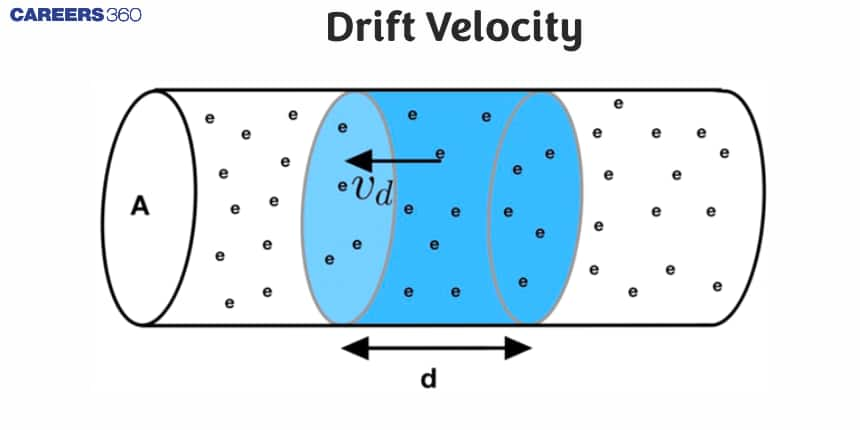
Drift Velocity - Meaning, Formula, FAQs

What is Drift Velocity Class 12?

Drift velocity definition: Drift velocity is the average velocity that a particle such as an electron attains in a material due to an electric field.

Drift velocity definition in terms of an electron: The drift velocity of an electron in a conductor is the average velocity an electron acquires in the presence of an electric field.

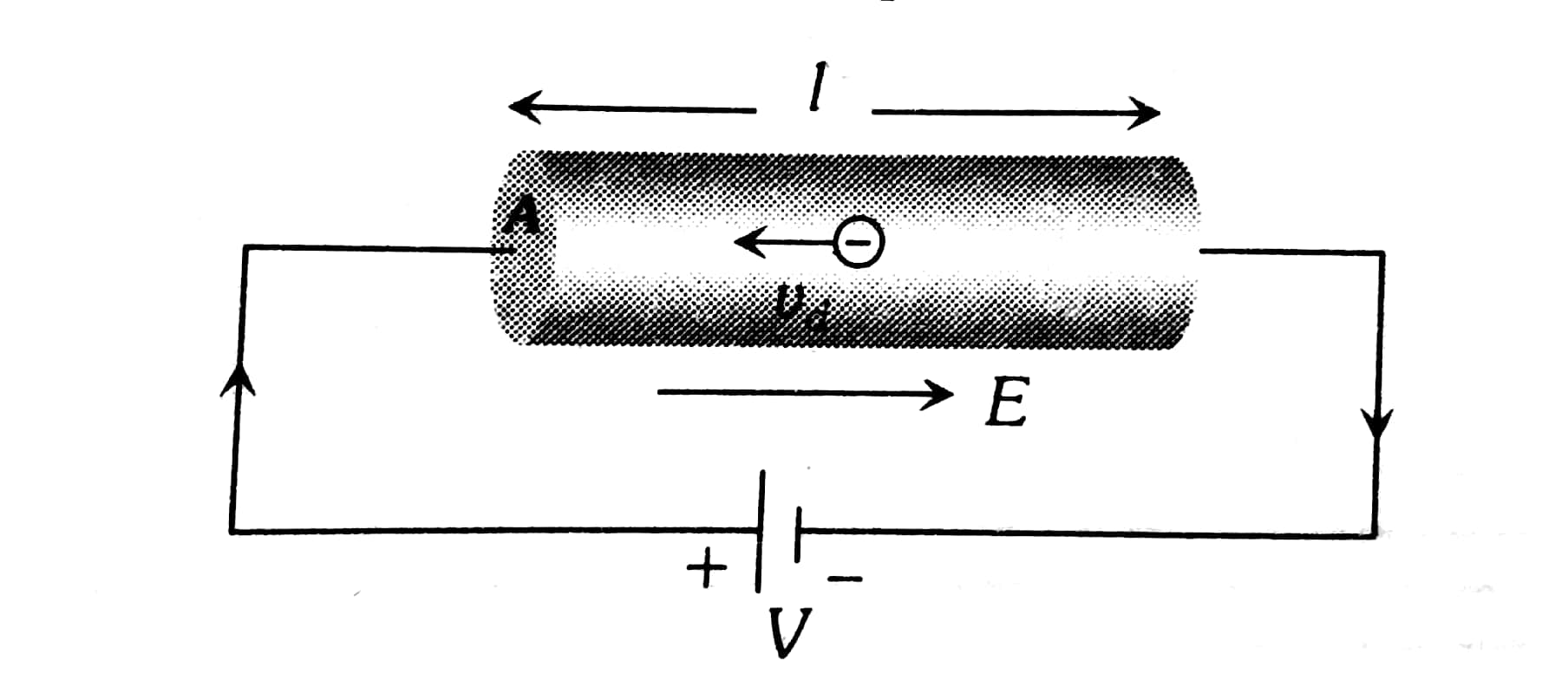
Drift Velocity Formula Class 12

$$V_d=\frac{I}{n A e}$$

where,

$V_d$ is the drift velocity of the electrons
$I$ is the electric current flowing through the conductor
$n$ is the number density of free electrons
$A$ is the cross-sectional area of the conductor
$e$ is the charge of an electron

Drift velocity in terms of electric field ($E$) and mobility of electrons ($\mu$)

$$
V_d=\mu E
$$

$V_d$ is directly proportional to $E$:

$V_d \propto E$ when the temperature is constant, the greater the electric field, the larger the drift velocity.

Drift velocity varies inversely with the area of the cross-section

Drift velocity

Also, read

SI Unit of Drift Velocity

The SI unit of drift velocity is meters per second ( $\mathrm{m} / \mathrm{s}$ ).

$V_d=\frac{I}{n A e}$

substituting unit of each term

$V_d=\frac{\mathrm{A}}{\left(\mathrm{m}^{-3}\right)\left(\mathrm{m}^2\right) \mathrm{C}}$

$V_d=\frac{\mathrm{A}}{\mathrm{m}^{-1} \cdot \mathrm{C}}$

$V_d=\frac{\mathrm{C} / \mathrm{s}}{\mathrm{m}^{-1} \cdot \mathrm{C}}$

Thus simplifying we get

$$V_d=\frac{\mathrm{m}}{\mathrm{s}}$$

Relation Between Current Density and Drift Velocity

The drift velocity is directly proportional to the current density.

$$
J=n e V_d
$$

where,

$J$ is the Current Density
$n$ is the number density of electrons in a conductor
$e:$ is the charge of an electron
$V_d$ is the drift velocity

Relation Between Drift Velocity and Electric Current

The drift velocity is directly proportional to the electric current.

$$
I=n A e v_d
$$

hence,

$$
I \propto v_d
$$

Factors Affecting Drift Velocity

Electric field
Charge of the electron
The number density of electrons
Temperature
Mobility of electron

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

Important Terms Related to Drift Velocity

Relaxation Time (τ):

The time interval between two successive collisions of electrons with the Positive ions.

Mean Free Path:

The path between two consecutive collisions is called the free path. The average length of these free paths is called the “Mean Free Path”.

Mobility Of An Electron:

It is the drift velocity of an electron per unit electric field. It indicates how easily an electron can pass through the material (conductor or semiconductor) in the presence of an electric field.

$$\mu=\frac{v_d}{E}$$

Solved Examples Based on Drift Velocity

Example 1: Drift speed of electrons, when 1.5 A of current flows in a copper wire of cross-section is v . If the electron density in copper is $9 \times 1028 / \mathrm{m} 3$ the value of $v$ in $\mathrm{mm} / \mathrm{s}$ is close to (Take charge of an electron to be $=1.6 \times 10-19 \mathrm{C}$ )

1) 0.02

2) 3

3) 2

4) 0.2

Solution:

$\begin{gathered}I=n e A V_d \\ V_d=\frac{I}{n e A}=\frac{9 \times 10^{28} \times 1.6 \times 10^{-19} \times 5 \times 10^{-6}}{1}=0.02 \times 10^{-3} \mathrm{~m} / \mathrm{s}=0.02 \mathrm{~mm} / \mathrm{sec}\end{gathered}$

Hence, the answer is the option (1).

Example 2: A current of 10 A exists in a wire of a cross-sectional area of 5 mm 2 with a drift velocity of $2 \times 10-3 \mathrm{~ms}-1$. The number of free electrons in each cubic meter of the wire is:

1) 1×1023
2) 625×1025
3) 2×1025
4) 2×106

Solution:

\begin{aligned}
&i=10 \mathrm{~A}, A=5 \mathrm{~mm}^2=5 \times 10^{-6} \mathrm{~m}^2 \text { and } v_d=2 \times 10^{-3} \mathrm{~m} / \mathrm{s}\\
&\text { We know, }\\
&\begin{gathered}
i=n e A v_d \\
10=n \times 1.6 \times 10^{-19} \times 5 \times 10^{-6} \times 2 \times 10^{-3} \Rightarrow n=0.625 \times 10^{28}=625 \times 10^{25}
\end{gathered}
\end{aligned}

Hence, the answer is the Option(2).

Example 3: When a 5 V potential difference is applied across a wire of length 0.1 m, the drift speed of electrons is $2.5 \times 10^{-4} \mathrm{~ms}^{-1}$. If the electron density in the wire is $8 \times 10^{28} \mathrm{~m}^{-3}$, the resistivity of the material is close to:

1) $1.6 \times 10-8 \Omega \mathrm{~m}$
2) $1.6 \times 10-7 \Omega \mathrm{~m}$
3) $1.6 \times 10-6 \Omega \mathrm{~m}$
4) $1.6 \times 10-5 \Omega \mathrm{~m}$

Solution:

\begin{aligned}
& I=A n e v_{-} d \\
& \Rightarrow V=R A n e v_{-} d \\
& \Rightarrow V(\rho I / A)=A n e v_{-} d \\
& \Rightarrow V A / \rho I=A n e v_{-} d \\
& \Rightarrow \rho=V / I^*\left(1 / n v_{-} d\right) \\
& \Rightarrow \rho=V I /\left(n e v_{-} d\right) \\
& =50.1 \times\left(8 \times 10^{\wedge} 28\right) \times\left(1.6 \times 10^{\wedge}(-19)\right) \times\left(2.5 \times 10^{\wedge}(-4)\right) \\
& \Rightarrow \rho=1.5625 \times 10^{\wedge}(-5) \Omega \mathrm{m} \approx 1.6 \times 10^{\wedge}(-5) \Omega \mathrm{m}
\end{aligned}

Hence, the answer is the option (4).

Example 4: An electron moving in a zigzag path travels a displaces by 0.2 mm in 10 seconds. Its drift speed is (in $\mathrm{m} / \mathrm{sec}$ )
1) $2 \times 10^{-5}$
2) $10^{-5}$
3) $2 \times 10^{-4}$
4) $10^{-4}$

Solution:

Drift velocity

Drift velocity is the average velocity that a particle such as an electron attains in a material due to an electric field.

wherein

drift velocity

Drift Velocity = Displacement/time

Displacement $=.2 \mathrm{~mm}=2 \times 10^{-4} \mathrm{~m}$

Time = 10 sec

Drift Velocity $V_d=2 \times 10^{-5} \mathrm{~m} / \mathrm{sec}$

Hence, the answer is option (1).

Example 5: Which of the following is correct regarding relaxation time?

1) Relaxation time increases with increase in temperature

2) Relaxation time decreases with increase in temperature

3) A decrease in relaxation time causes a decrease in resistivity

4) Conductivity is independent of Relaxation time

Solution:

Relaxation time ($\tau$)⟶ The time interval between two successive collisions of electrons with the ions/ atoms.

As with an increase in temperature drift velocity increases which will lead to an increase in the rate of collision and hence relaxation time decreases.

Hence, the answer is the option (2).

Frequently Asked Questions (FAQs)

1. What is the definition of mobility in physics?

The ease with which a specific type of charged particle moves through a material under the influence of an electric field is referred to as mobility in physics. Electric fields attract these particles, which interact with solid molecules on a regular basis. The average speed at which the particles travel as a result of the electric field and collision is known as drift speed. In most metals, the charge carrier is a negatively charged electron.

Electron mobility is used to determine how rapidly an electron moves through a metal or semiconductor under the influence of an electric field.

Electron mobility is expressed mathematically as: μ=VdE .

Where vd is the electron's drift velocity and E is the external electric field.

The Si unit of mobility is the m²v^-1s^-1.

2. Is Drift velocity Affected by Diameter?

Any conductor's drift velocity is independent of its cross-sectional area or diameter..

3. What causes such a low drift velocity?

The average velocity that an electron achieves as a result of an electric field is known as the electron drift velocity. The average velocity, or electron drift velocity, is very low due to collisions between electrons.

4. What is Drift current and how does it work?

The electric current produced by particles being dragged by an electric field is known as drift current. Although the phrase is most usually associated with electrons and holes in semiconductors, the concept can also be applied to metals, electrolytes, and other materials.

5. What's the relationship between drift velocity and electric field strength?

Drift velocity is directly proportional to electric field strength. A stronger electric field exerts more force on the charge carriers, accelerating them more between collisions and resulting in a higher average velocity in the field direction.

6. What's the relationship between drift velocity and electron mean free path?

The mean free path, which is the average distance an electron travels between collisions, is directly related to drift velocity. A longer mean free path generally results in higher drift velocity as electrons can accelerate more between collisions.

7. Why doesn't drift velocity depend on the length of the conductor?

Drift velocity is independent of conductor length because it's determined by local conditions like electric field strength and material properties. Changing the length affects the total voltage needed to maintain the same electric field, but not the drift velocity itself.

8. How does drift velocity affect power transmission in electrical grids?

Understanding drift velocity is important in power transmission as it relates to current density and power losses. Lower drift velocities for a given current can be achieved with larger conductor cross-sections, reducing resistive losses in long-distance transmission.

9. How does the relaxation time of electrons affect drift velocity?

The relaxation time, which is the average time between electron collisions, directly affects drift velocity. A longer relaxation time allows electrons to accelerate more between collisions, resulting in a higher drift velocity.

10. Why is drift velocity typically much slower than the actual speed of electrons?

Drift velocity is slow because electrons frequently collide with atoms in the conductor, changing direction randomly. The net movement in one direction is small compared to their total path length, resulting in a low average velocity in the direction of current flow.

11. Can drift velocity be zero when electrons are moving?

Yes, drift velocity can be zero even when electrons are moving. This occurs when there's no net electric field applied, causing electrons to move randomly with no preferred direction, resulting in zero average velocity.

12. How does temperature affect drift velocity?

Increasing temperature generally decreases drift velocity. Higher temperatures cause more frequent collisions between electrons and atoms, increasing resistance and reducing the net movement of charge carriers in the direction of the electric field.

13. Why doesn't increasing voltage indefinitely increase drift velocity?

Increasing voltage does increase drift velocity initially, but it doesn't continue indefinitely. At very high voltages, other factors like electron-electron interactions and relativistic effects come into play, limiting further increases in drift velocity.

14. What's the relationship between drift velocity and conductor cross-sectional area?

Drift velocity is inversely proportional to the cross-sectional area of the conductor. For a given current, a larger cross-sectional area means more electrons can flow, resulting in a lower drift velocity for each electron.

15. What's the difference between drift velocity and electron velocity?

Drift velocity is the average velocity of electrons in a specific direction due to an applied electric field, while electron velocity refers to the actual speed of individual electrons, which is much higher and includes random thermal motion.

16. Can drift velocity be negative?

Yes, drift velocity can be negative. The sign of drift velocity indicates the direction of net charge carrier movement. A negative drift velocity means the charge carriers are moving in the direction opposite to the conventional current flow.

17. What's the significance of drift velocity in understanding electrical resistance?

Drift velocity helps explain electrical resistance. As electrons drift through a conductor, they collide with atoms, transferring energy and creating resistance. The slower the drift velocity, the more time for collisions, resulting in higher resistance.

18. How does the concept of drift velocity apply to semiconductors?

In semiconductors, drift velocity applies to both electrons and holes. The overall current is a result of the drift of both types of charge carriers, each with its own drift velocity, which can be different due to their different effective masses.

19. Why is drift velocity important in the design of electronic devices?

Understanding drift velocity is crucial in electronic device design as it affects current density, power dissipation, and signal propagation speed. It helps engineers optimize device performance and predict behavior under different operating conditions.

20. What's the connection between drift velocity and current density?

Current density is directly related to drift velocity. It's calculated as the product of charge carrier density, charge per carrier, and drift velocity. Higher drift velocity leads to higher current density for a given charge carrier concentration.

21. How does the mass of charge carriers affect drift velocity?

Heavier charge carriers will have a lower drift velocity compared to lighter ones under the same electric field. This is because more massive particles accelerate more slowly in response to the applied force.

22. How does drift velocity relate to the concept of mobility in solid-state physics?

Mobility is defined as the ratio of drift velocity to electric field strength. It represents how easily charge carriers move through a material in response to an applied electric field, with higher mobility indicating higher drift velocity for a given field.

23. How does drift velocity change in a superconductor?

In a superconductor, the concept of drift velocity changes dramatically. Electrons form Cooper pairs that can move through the material without resistance, leading to potentially much higher effective drift velocities compared to normal conductors.

24. How does the concept of drift velocity apply to alternating current (AC)?

In AC, the drift velocity of electrons oscillates back and forth with the changing electric field. The average drift velocity over a complete cycle is zero, but the instantaneous drift velocity varies sinusoidally with the AC frequency.

25. How does drift velocity relate to current intensity?

Drift velocity is directly proportional to current intensity. As the current increases, the drift velocity of electrons also increases, indicating a faster net movement of charge carriers through the conductor.

26. How does the concept of drift velocity relate to Ohm's law?

Drift velocity helps explain Ohm's law at a microscopic level. The linear relationship between current and voltage in Ohm's law arises from the proportional relationship between drift velocity and electric field strength in many materials.

27. Can drift velocity be measured directly?

Direct measurement of drift velocity is challenging. It's typically calculated indirectly from measurable quantities like current, charge carrier density, and conductor properties. Some advanced techniques, like Hall effect measurements, can provide estimates.

28. How does the free electron density in a conductor affect drift velocity?

Higher free electron density generally leads to lower drift velocity for a given current. With more electrons available to carry current, each individual electron needs to move less quickly to maintain the same overall current flow.

29. What role does drift velocity play in the Hall effect?

Drift velocity is crucial in understanding the Hall effect. When a magnetic field is applied perpendicular to the current flow, it exerts a force on the drifting charge carriers, causing a voltage difference perpendicular to both the current and magnetic field.

30. What is drift velocity in the context of electric current?

Drift velocity is the average velocity at which electrons move through a conductor when an electric field is applied. It represents the net movement of charge carriers in a specific direction, contributing to electric current flow.

31. What's the significance of drift velocity in semiconductor device physics?

In semiconductor devices, understanding drift velocity is crucial for designing and optimizing components like transistors. It affects carrier transport, device speed, and performance characteristics, especially in high-frequency applications.

32. How does the concept of drift velocity apply to plasma physics?

In plasmas, both ions and electrons contribute to current flow, each with its own drift velocity. The much lighter electrons typically have much higher drift velocities than the heavier ions, leading to complex charge dynamics in plasma systems.

33. How does drift velocity compare in metals and electrolytes?

Drift velocity in metals is typically higher than in electrolytes. In metals, electrons are the charge carriers, while in electrolytes, larger ions carry the charge. The smaller mass and size of electrons allow for higher drift velocities in metals.

34. Can drift velocity be different for different types of charge carriers in the same material?

Yes, different charge carriers (e.g., electrons and holes in semiconductors) can have different drift velocities in the same material due to differences in their effective masses and mobilities.

35. Can drift velocity exceed the speed of light?

No, drift velocity cannot exceed the speed of light. Even in superconductors or under extremely high electric fields, the drift velocity remains well below the speed of light due to fundamental physical limitations.

36. Why isn't drift velocity uniform throughout a conductor?

Drift velocity can vary within a conductor due to factors like non-uniform electric fields, variations in conductor geometry, or local differences in temperature or impurity concentration, which affect electron mobility.

37. How does the concept of drift velocity help explain the skin effect in conductors?

Drift velocity helps explain the skin effect, where high-frequency currents tend to flow near the surface of a conductor. This occurs because the changing magnetic field induces eddy currents that affect the drift velocity distribution across the conductor's cross-section.

38. How does drift velocity relate to the concept of electrical conductivity?

Electrical conductivity is directly related to drift velocity. Materials with higher conductivity allow charge carriers to achieve higher drift velocities for a given electric field, resulting in greater current flow.

39. What's the relationship between drift velocity and the Drude model of electrical conduction?

The Drude model uses the concept of drift velocity to explain electrical conduction in metals. It assumes that electrons move freely between collisions with ions, with their average velocity (drift velocity) determined by the applied electric field and collision frequency.

40. How does drift velocity affect the operation of solar cells?

In solar cells, understanding drift velocity is important for optimizing charge carrier collection. The drift velocity of electrons and holes, influenced by the built-in electric field, affects how efficiently photogenerated carriers can be collected before recombination.

41. What role does drift velocity play in thermoelectric effects?

Drift velocity is relevant to thermoelectric effects like the Seebeck effect. Temperature gradients can cause differences in drift velocities of charge carriers, leading to a buildup of charge and the generation of a voltage difference across the material.

42. How does the concept of drift velocity apply to two-dimensional materials like graphene?

In 2D materials like graphene, the concept of drift velocity applies but can behave differently due to unique band structures. Graphene, for instance, can exhibit very high drift velocities due to its high electron mobility and linear dispersion relation.

43. What's the connection between drift velocity and the mean collision time of electrons?

The mean collision time is inversely related to drift velocity. A longer mean collision time allows electrons to accelerate more under the electric field before colliding, resulting in a higher average drift velocity.

44. How does drift velocity affect the frequency response of electronic components?

Drift velocity influences the frequency response of electronic components by affecting the time it takes for charge carriers to traverse the device. Higher drift velocities generally allow for better high-frequency performance in devices like transistors.

45. Can drift velocity be used to explain the difference between conductors and insulators?

Yes, the concept of drift velocity helps explain the difference between conductors and insulators. In conductors, electrons can achieve significant drift velocities under an applied electric field. In insulators, the drift velocity is negligible due to the lack of free charge carriers.

46. How does drift velocity relate to the concept of electron ballistic transport?

Drift velocity and ballistic transport represent different regimes of electron movement. Drift velocity applies when electrons undergo frequent collisions, while ballistic transport occurs when electrons can travel through a material without collisions, typically in very small or highly pure devices.

47. What's the significance of drift velocity in understanding current saturation in semiconductors?

Drift velocity is key to understanding current saturation in semiconductors. As the electric field increases, drift velocity initially increases linearly but eventually saturates due to increased scattering at high fields, leading to a limit on the maximum current density.

48. How does the concept of drift velocity apply to nanoscale electronic devices?

In nanoscale devices, the traditional concept of drift velocity may break down as the device dimensions become comparable to or smaller than the mean free path of electrons. Quantum effects and ballistic transport can become more significant in these cases.

49. What's the relationship between drift velocity and the relaxation time approximation in solid-state physics?

The relaxation time approximation assumes that electrons return to equilibrium after a characteristic time following a collision. This approximation is used to derive the expression for drift velocity in terms of the electric field and the average time between collisions.

50. How does drift velocity contribute to Joule heating in electrical conductors?

Drift velocity is directly related to Joule heating. As electrons drift through a conductor, they collide with atoms, transferring kinetic energy. This energy transfer manifests as heat, with the power dissipated proportional to the square of the drift velocity.

51. Can the concept of drift velocity be applied to superconducting quantum interference devices (SQUIDs)?

While traditional drift velocity doesn't apply in superconductors, the concept is relevant in understanding SQUID operation. The movement of Cooper pairs in response to applied fields and the quantum interference effects are analogous to drift velocity in normal conductors.

52. How does drift velocity affect the performance of field-effect transistors (FETs)?

In FETs, drift velocity is crucial for device performance. It affects the transit time of carriers through the channel, influencing the maximum operating frequency and switching speed of the transistor. Velocity saturation at high fields is a key factor in FET design.

53. What's the significance of drift velocity in understanding electrical noise in conductors?

Drift velocity contributes to our understanding of electrical noise. Fluctuations in drift velocity due to random thermal motion and collisions give rise to thermal noise (Johnson-Nyquist noise) in conductors, which sets fundamental limits on signal detection in electronic systems.

54. How does the concept of drift velocity help in explaining the operation of magnetohydrodynamic generators?

In magnetohydrodynamic generators, the concept of drift velocity is applied to the movement of charged particles in a conductive fluid or plasma. The interaction between the drifting charges and a magnetic field is used to generate electricity, with the drift velocity determining the current density and power output.