Calculation Of Resistance By Symmetry

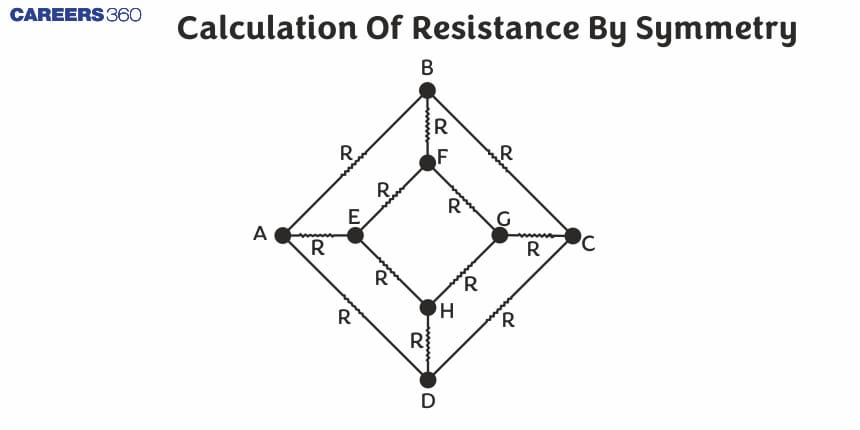
Calculation of Resistance by Symmetry

In the study of electrical circuits, the calculation of equivalent resistance in complex networks can often be daunting. However, symmetry provides a clever and efficient method to simplify these calculations. When a circuit exhibits symmetry, certain components or sections can be grouped or considered identical in their contribution to the overall resistance. This approach reduces the complexity of the problem and leads to quicker, more intuitive solutions.

Vertical Plane of Symmetry

1. Points on a vertical plane of symmetry have the same potential

2. Branches which are mirror images of the vertical plane of symmetry have the same current

The Horizontal Plane of Symmetry

Points which are mirror images of the horizontal plane of symmetry have the same potential.

Recommended Topic Video

Solved Examples Based on Calculation of Resistance By Symmetry

Example 1:

Four resistances $40 \Omega, 60 \Omega, 90 \Omega$ and $110 \Omega$ make the arms of a quadrilateral ABCD. Across AC is a battery of EMF 40V and internal resistance negligible. The potential difference across BD in V is_____________.

1) 2

2) 4

3) 6

4) 8

Solution:

$\begin{aligned} & i_1=\frac{40}{40+60}=0.4 \\ & i_2=\frac{40}{90+110}=\frac{1}{5} \\ & v_B+i_1(40)-i_2(90)=v_D \\ & v_B-v_D=\frac{1}{5}(90)-\frac{4}{10} \times 40 \\ & v_B-v_D=18-16=2\end{aligned}$

Hence, the answer is the option (1).

Example 2: The power dissipated in the branch CD is?

1) $\frac{V^2}{R}$
2) $\frac{V^2}{2 R}$
3) Zero
4) $\frac{3 V^2}{2 R}$

Solution:

Calculation of Resistance by Symmetry

Vertical Plane of symmetry:

1. Points on the vertical plane of symmetry have the same potential

2. Branches which are mirror images of the vertical plane of symmetry have the same current

Since the circuit is symmetrical about CD there is no current through CD. So power equals zero.

Hence, the answer is the option (3).

Example 3: Find the equivalent resistance between A and B

1) $\frac{8 R}{3}$
2) $\frac{2 R}{3}$
3) $\frac{R}{3}$
4) $\frac{5 R}{3}$

Solution:

Calculation of Resistance by Symmetry

Calculation of Resistance by Symmetry

Resistance by Symmetry:

Vertical Plane of symmetry:

1. Points on the vertical plane of symmetry have the same potential

2. Branches which are mirror images of the vertical plane of symmetry have the same current

The horizontal plane of symmetry: Points which are mirror images of the horizontal plane of symmetry have the same potential.

Due to symmetry along the plane, CA and potential at O and A are the same. Therefore the potential difference between O and A is zero. So we can eliminate the resistance between O and A. Now simplifying the circuit the net resistance between A and B equals 2R/3

Hence, the answer is the option (2).

Example 4: In the given figure switches $S_1$ and $S_2$ are in open condition. The resistance across ab when the switches $S_1$ and $S_2$ are closed is ______________$\Omega.$

1) 10

2) 12

3) 14

4) 16

Solution:

When $S_1 \& S_2$ are closed

$\begin{aligned} & R_1=\frac{12 \times 6}{12+6}=4 \\ & R_2=\frac{4 \times 4}{4+4}=2 \\ & R_3=\frac{6 \times 12}{6+12}=4 \\ & R_{a b}=10 \Omega\end{aligned}$

Hence, the answer is the option (1).

Example 5: In the given figure, the emf of the cell is 2.2 V and if internal resistance is $0 \cdot 6 \Omega$ calculate the power dissipated in the whole circuit:

1) 1.32 W
2) $4 \cdot 4 \mathrm{~W}$
3) $0 \cdot 65 \mathrm{~W}$
4) $2 \cdot 2 \mathrm{~W}$

Solution:

Let the potential of pf a & B be X & Y respectively

$\begin{aligned} & \frac{1}{R_{A B}}=\frac{1}{6}+\frac{1}{12}+\frac{1}{4}+\frac{1}{8} \\ & =\frac{8+4+12+6}{48} \\ & \frac{1}{R_{A B}}=\frac{30}{48} \\ & R_{A B}=\frac{8}{5}=1 \cdot 6 \Omega \\ & I=\frac{2 \cdot 2 V}{R_{A B}+r}=\frac{2 \cdot 2}{1 \cdot 6+0 \cdot 6}=1 \mathrm{~A} \\ & \text { Total Power Dissipated }=I^2\left(R_{A B}+r\right) \\ & =1(2 \cdot 2) \\ & =2 \cdot 2 \mathrm{~W} \\ & \end{aligned}$
Hence, the answer is the option (4).

Summary

Calculating resistance by symmetry simplifies complex electrical circuits by identifying symmetrical patterns, allowing for quicker and more intuitive solutions. By recognizing vertical and horizontal planes of symmetry, we can determine potential differences, currents, and equivalent resistances in a circuit. This method is particularly useful for analyzing intricate networks and ensuring efficient circuit design in real-world applications