Kirchhoff’s Law - Equation, Example, FAQs

Overview Of Gustav Robert Kirchoff and His Circuital Laws

Kirchhoff's circuit rules are two equalities that deal with the electric current and potential difference in the lumped element model of electrical circuits (often known as voltage).In 1845, a German scientist named Gustav Robert Kirchhoff was the first to describe them. This broadened Georg Ohm's work and came before James Clerk Maxwell's. Kirchhoff's rules, often known as Kirchhoff’s laws, are widely utilized in electrical engineering. These rules apply in both time and frequency domains and serve as the foundation for network analysis.
Kirchhoff’s current law (KCL LAW) and Kirchhoff’s voltage law (KVL LAW) were defined in 1845 after he pursued the notions of Ohm's law and Maxwell's law.
Kirchhoff’s current law, or KCL LAW, is based on the principle of electric charge conservation. The input current to a node must be equal to the node's output current, according to this rule.

What Are Kirchhoff’s Laws?

In 1845, German physicist Gustav Kirchhoff introduced two important laws that explain how current and energy are conserved in electrical circuits. These are known as Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL). They are very useful for analyzing complex electrical networks and finding unknown currents and voltages.

• Kirchhoff’s Current Law (KCL): Also called the Junction Rule or First Law, it states that the total current entering a junction equals the total current leaving the junction. This follows the law of conservation of charge.
  
• Kirchhoff’s Voltage Law (KVL): Also called the Loop Rule or Second Law, it states that the sum of all voltages around a closed loop is zero. This follows the law of conservation of energy.

Kirchhoff’s First Law or Kirchhoff’s Current Law (KCL LAW)

Kirchhoff’s current law definition: - The current coming into a node (or a junction) must match the current flowing out of it, according to Kirchhoff's first law. This is due to charge conservation.

The conventional technique to explain Kirchhoff’s current law is to write Kirchhoff’s equation in which the sum of all currents entering the junction equals the sum of currents exiting the junction.

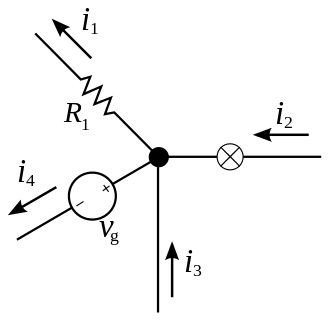
From the figure, the circuit consists of a junction with four branches. Currents $i_1, i_2, i_3$, and $i_4$ flow through these branches, involving a resistor $R_1$, a voltage source $V_g$, and other components. Kirchhoff's Current Law can be applied at the junction to relate the incoming and outgoing currents.

The current that enters a junction equals the current that leaves that junction.

$i_1+i_4=i_2+i_3$

This can be generalized to n wires joined together at a node, so Kirchhoff's current law formula is given as,

$
\sum_{k=1}^n i_k=0
$

Kirchhoff’s Second Law or Kirchhoff’s Voltage Law (KVL LAW)

Kirchhoff’s voltage law definition: - The sum of all voltages across components that supply electrical energy (such as cells or generators) in any entire loop inside a circuit must match the sum of all voltages across all other components in the same loop, according to Kirchhoff’s voltage law (2nd Law). This law is the result of both charge and energy conservation.

When there are multiple junctions in a circuit, we must be careful to apply this law to only one loop at a time. In practice, this means selecting only one option at each crossroads. In the diagram given below, the circuit is a closed loop consisting of resistors $R_1, R_2, R_3$, and $R_5$ connected between nodes $a, b, c, d$, along with a voltage source $V_4$ between nodes $a$ and $d$. The currents flow through the resistors and are governed by the voltage drops $v_1, v_2, v_3$, and $v_5$ across each resistor, as determined by Kirchhoff's Voltage Law.

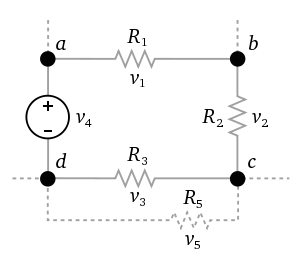
The total of all voltages around a loop equals zero.

$v_1+v_2+v_3+v_4=0$

Kirchhoff’s voltage law formula can be generalized.

$\sum_{k=1}^n V_k=0$

Applications of Kirchhoff’s Laws

Kirchhoff’s laws are widely used in electrical and electronic circuit analysis. Some important applications are:

• Complex Circuit Analysis: Used to calculate current and voltage in circuits with multiple loops and junctions.
• Bridge Circuits: Applied in Wheatstone bridges to determine unknown resistances.
• Electrical Networks: Helps in analyzing series-parallel networks and finding equivalent resistances.
• AC and DC Circuits: Used in both alternating current (AC) and direct current (DC) circuits for calculating currents, voltages, and impedances.
• Electronics Design: Useful in designing amplifiers, filters, and electronic devices by analyzing current flow and voltage drops.

Limitations of Kirchhoff’s laws

Both Kirchhoff’s laws contain a constraint in that they work under the premise that the closed loop has no fluctuating magnetic field. In the presence of a fluctuating magnetic field, electric fields, and emf can be induced, causing Kirchhoff’s loop rule to fail.

Other limitations are:

• Applicable to lumped circuits only
• High-frequency limitations
• Difficult for complex circuits

Recommended Topic Video

Solved Example Based on Kirchhoff's Laws

1. Consider a circuit with a 12 V battery and two resistors, $R_1=4 \Omega$ and $R_2=6 \Omega$, connected in parallel. Find the current through each resistor using Kirchhoff's Current Law (KCL) and Kirchhoff's Voltage Law (KVL).

Solution:
Using KVL
In parallel circuits, the voltage across each resistor is equal to the battery voltage:

$
V_1=V_2=12 \mathrm{~V}
$

Using Ohm's Law (from KVL)

$
\begin{aligned}
& I_1=\frac{V}{R_1}=\frac{12}{4}=3 \mathrm{~A} \\
& I_2=\frac{V}{R_2}=\frac{12}{6}=2 \mathrm{~A}
\end{aligned}
$

Using KCL at the junction
The total current supplied by the battery is the sum of branch currents:

$
I_{\text {total }}=I_1+I_2=3+2=5 \mathrm{~A}
$

Related Topics,

• Difference Between Resistance and Resistivity
• Electrical Energy and Power
• Electrical Resistance
• Electromotive Force
• Ohm's Law