Current Electricity - Topics, Formulas, Notes, Books, FAQs
Look around you and you will realize that you are surrounded with many electronic gadgets like mobile phone, TV or laptop etc. All of these devices will stop working if they won’t have an energy source or a battery. This energy comes in the form of electric current. Not only that nature also has many types of currents like the lightning in the clouds is a result of the uncontrolled flow of charges to earth.
Current Electricity Class 12th Topics(NCERT Syllabus)
Current Electricity Class 12 explain the flow of electric charges in conductors. In this chapter you will learn the concepts like electric current, drift velocity, Ohm’s law, resistance, resistivity and electrical energy. This Chapter also covers series and parallel combinations of resistors, Kirchhoff’s laws and applications in circuits. These topics build the foundation for understanding electrical devices and solving both numerical and theoretical problems in physics.
1. Introduction
When we switch on a bulb, charge flows through the wire and the bulb starts glowing. Similarly, mobile phones, fans, and computers all work because of the continuous flow of charges. This flow of charges is called current electricity. It deals with the study of electric current, resistance, potential difference, and the laws governing current in circuits.
2. Electric Current
Electric current is the rate of flow of electric charge through a conductor. If a charge $q$ flows across any cross-section of a conductor in time $t$, then the current is given by
$$
I=\frac{q}{t}
$$
Its SI unit is ampere $(\mathrm{A})$, where $1 \mathrm{~A}=1 \mathrm{Coulomb} /$ second. Electric current is a scalar quantity, and it always flows from higher potential to lower potential in a conductor.
3. Electric Currents in Conductors
In conductors like metals, free electrons move randomly in all directions when no potential difference is applied. These random motions cause no net current. When a potential difference is applied across the conductor, the free electrons experience a force and drift slowly in a particular direction, giving rise to an electric current.
4. Ohm's Law
Ohm's law states that the current flowing through a conductor is directly proportional to the potential difference applied across its ends, provided temperature and other physical conditions remain constant.
$$
V \propto I \quad \text { or } \quad V=I R
$$
5. Drift of Electrons and the Origin of Resistivity
In a conductor, free electrons move randomly, so there is no net current. When an electric field $E$ is applied, electrons acquire a small drift velocity ( $v_d$ ) opposite to the field. This drift motion produces a steady current.
The drift velocity is given by:
$$
v_d=\frac{e E \tau}{m}
$$
6. Limitations of Ohm's Law
Ohm's law is not universally applicable. Its limitations are:
1. It is valid only when temperature, pressure, and other physical conditions remain constant.
2. It does not apply to non-ohmic devices such as diodes, transistors, and vacuum tubes, where $V-I$ relation is not linear.
3. It fails for electrolytes, gases, and semiconductors, since their current does not vary linearly with applied voltage.
4. At very high voltages or in strong electric fields, the proportionality between $V$ and $I$ breaks down.
7. Resistivity of Various Materials
Resistivity $(\rho)$ is a property of a material that opposes the flow of electric current. It varies for different substances:
1. Conductors (e.g., copper, silver, aluminum): Very low resistivity $\left(10^{-8} \Omega m\right) \rightarrow$ allow current to flow easily.
2. Semiconductors (e.g., silicon, germanium): Moderate resistivity $\rightarrow$ can act as conductor or insulator depending on conditions.
3. Insulators (e.g., rubber, wood, glass): Very high resistivity ( $10^8 \Omega \mathrm{~m}$ or more) $\rightarrow$ do not allow current to pass.
8. Temperature Dependence of Resistivity
The resistivity of a material changes with temperature:
1. Metals: Resistivity increases with rise in temperature because atoms vibrate more, causing more collisions of electrons.
$$
\rho_T=\rho_0\left[1+\alpha\left(T-T_0\right)\right]
$$
where $\alpha=$ temperature coefficient of resistivity.
2. Semiconductors & Insulators: Resistivity decreases with increase in temperature, since more charge carriers are released.
9. Electrical Energy and Power
in an actual conductor, an amount of energy dissipated as heat in the conductor during the time interval $\Delta t$ is,
$$
\Delta W=I V \Delta t
$$
The energy dissipated per unit time is the power dissipated $P=\Delta W / \Delta t$ and we have,
$$
P=I V
$$
10. Cells, EMF, Internal Resistance
A cell is a device that converts chemical energy into electrical energy.
- EMF (Electromotive Force): The total potential difference between the terminals of a cell when no current is drawn. It represents the maximum energy supplied per unit charge. Its SI unit is volt (V).
- Internal Resistance (r): The resistance offered by the electrolyte and electrodes inside the cell.
When a cell of EMF $E$ and internal resistance $r$ supplies current $I$ through an external resistance $R$ :
$$
\begin{gathered}
E=I(R+r) \\
V=I R=E-I r
\end{gathered}
$$
11. Cells in Series and in Parallel
- Cells in Series:
When cells are connected end-to-end (positive to negative), the effective EMF is the sum of individual EMFs, while internal resistances add up.
$$E_{\mathrm{eq}}=E_1+E_2+\ldots, \quad r_{\mathrm{eq}}=r_1+r_2+\ldots$$
- Cells in Parallel:
When cells are connected positive to positive and negative to negative, the effective EMF remains the same as that of a single cell, but internal resistance decreases.
$$E_{\mathrm{eq}}=E, \quad \frac{1}{r_{\mathrm{eq}}}=\frac{1}{r_1}+\frac{1}{r_2}+\ldots$$ - Grouping of cells
12. Kirchhoff's Rules
Kirchhoff's rules are used to solve complex electrical circuits:
1. Kirchhoff's Current Rule (KCL):
The total current entering a junction is equal to the total current leaving the junction.
$$
\sum I_{\mathrm{in}}=\sum I_{\mathrm{out}}
$$
This is based on conservation of charge.
2. Kirchhoff's Voltage Rule (KVL):
The algebraic sum of potential differences around any closed loop of a circuit is zero.
$$
\sum V=0
$$
This is based on conservation of energy.
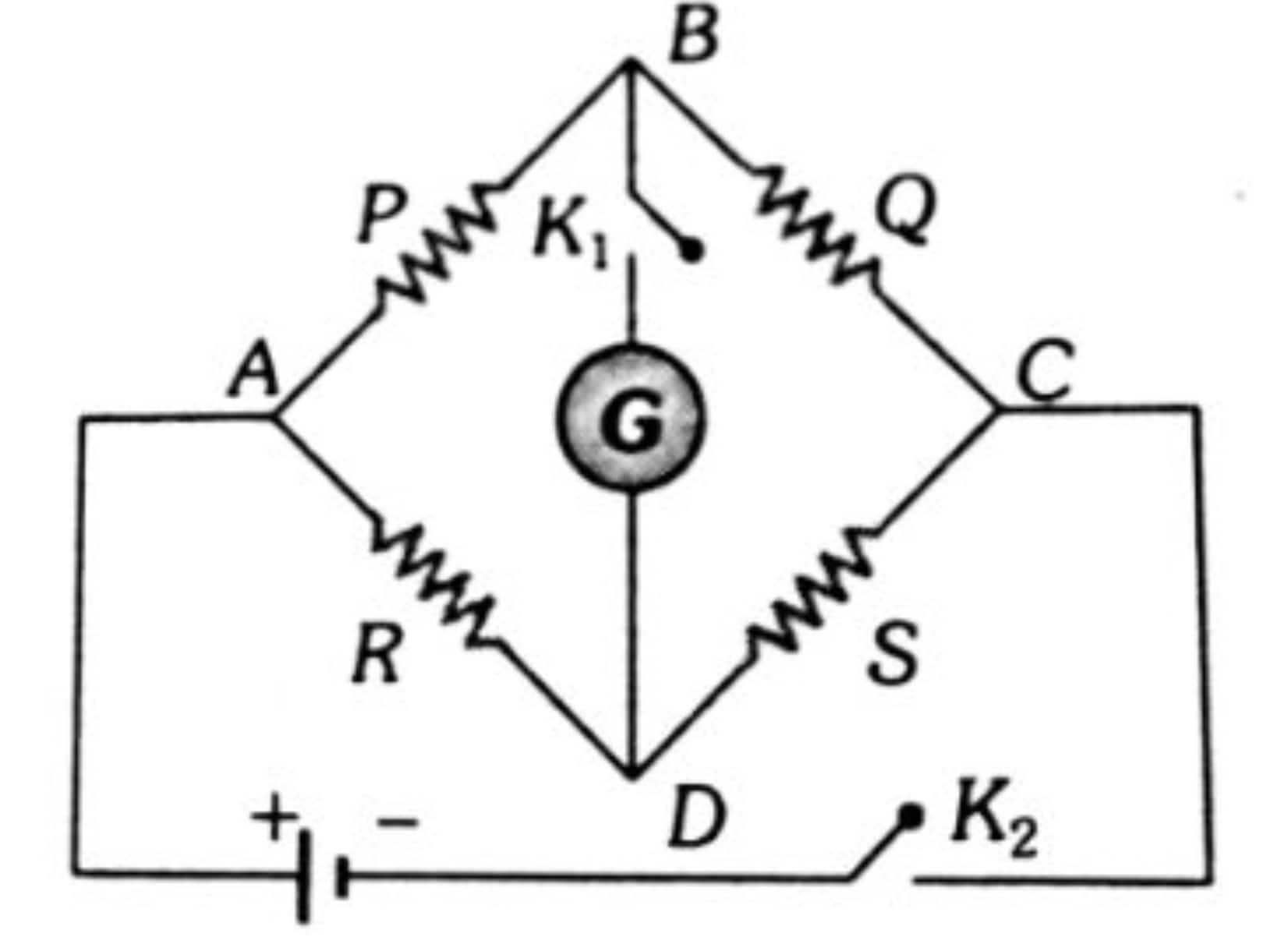
13. Wheatstone Bridge
The Wheatstone bridge is an arrangement of four resistors in the form of a quadrilateral, used to measure an unknown resistance accurately. A galvanometer is connected between the two opposite corners.
If resistors are $P, Q, R, S$, then the bridge is balanced (no current through galvanometer) when:
$$
\frac{P}{Q}=\frac{R}{S}
$$
| Also read, |
Formulas for Current & Electricity
-
Drift Velocity, $v_d=\frac{e E \tau}{m}$ where $\tau$ is relaxation time & E is Electric Field
-
Current in terms of drift velocity, $i=n e A v_d$ where n is free e- density.
- Current density, $j=\frac{i}{A}$
- Ohm's law, $\frac{V}{I}=R$
- Resistance, $R=\rho \frac{l}{A}$ where $\rho$ is resistivity
-
Equivalent Resistance
-
$\begin{aligned} & \text { Parallel arrangement, } \\ & \frac{1}{R_{e q}}=\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3} \ldots \ldots\end{aligned}$
-
$\begin{aligned} & \text { Series } \quad \text { arrangement, } \\ & R_{e q}=R_1+R_2+R_3 \ldots \ldots \ldots\end{aligned}$
-
- Power, $P=V I$
- Kirchhoff's junction rule, $\sum_{\text {junction }} i=0$
- Kirchhoff's loop rule,$
\sum_{\text {closed loop }} \Delta V=0
$
NCERT Notes Subject Wise Link:
Exam-wise Weightage of Current Electricity
| Exam | Approximate Weightage | Remarks |
|---|---|---|
| NEET | 1-2 Questions | Direct formula-based questions (Ohm’s law, power, resistance). Circuit analysis is usually simple. |
| Board | 6 marks | Derivations (Ohm’s law, resistivity, Wheatstone bridge) and short numericals are frequently asked. |
| JEE | 1-2 Question | Important for circuit problems; includes advanced applications of Kirchhoff’s rules, Wheatstone bridge, and combination of resistors/cells. |
How to prepare Current Electricity
Before solving questions of this chapter you should be well versed with the concepts of electrostatics, you should be able to find the equivalent capacitance and calculate the potential difference. This chapter is easy if you know the concepts of electrostatics. You will find many questions of this chapter which involve your practical knowledge, like questions on potentiometer, ammeter or voltmeter etc, so do your practicals very carefully and understand each and everything about it. If you are not able to do practicals then watch animated videos of working of all these electronic measuring devices. Many times you will be given complex circuits of resistors and you either have to solve for equivalent resistance, current or potential difference. So keep practicing questions on circuits.
Books for Current Electricity
For this chapter, I would recommend you to first go through NCERT book and your Lab manual and solve questions from those chapters. Then you should solve questions from NCERT Exemplar book for a good hold on this chapter. If you want to test yourself for competitive exams, then you should read Understanding Physics by D.C. Pandey.
NCERT Solutions Subject wise link:
- NCERT solutions for class 11 Physics.
- NCERT solutions for class 11 Chemistry.
- NCERT solutions for class 11 Mathematics.
- NCERT solutions for class 11 Biology.
NCERT Exemplar Solutions Subject wise link:
Frequently Asked Questions (FAQs)
Current Rule (KCL): Total current entering a junction equals total current leaving it.
Voltage Rule (KVL): Sum of voltages around a closed loop is zero.
Resistivity is a material property that measures how strongly a material opposes the flow of electric current. Metals have low resistivity, while insulators have high resistivity.
Yes, it is taught in Class 10th
Class 12 Current Electricity notes are available on the Career360 page, covering theory, formulas, and solved examples.
Current electricity is the flow of electric charges through a conductor, creating an electric current.