Electric Flux Through Cone Or Disc
Imagine you're standing in the rain, holding an umbrella. The amount of water that passes through the surface of the umbrella depends on how it's oriented and how much rain is falling. In the world of electric fields, a similar concept is known as electric flux, which measures how much of the electric field passes through a given surface.
This Story also Contains
- The electric flux through a cone or disc
- Solved Examples Based on Electric flux through Cone or Disc
- Example 1: A cylinder of radius R and length L is placed in a uniform electric field E parallel to the cylinder axis. The total flux for the surface of the cylinder is given by 1) 2πR2E 2) πR2/E 3) (πR2−πR)/E 4) zero
- Summary
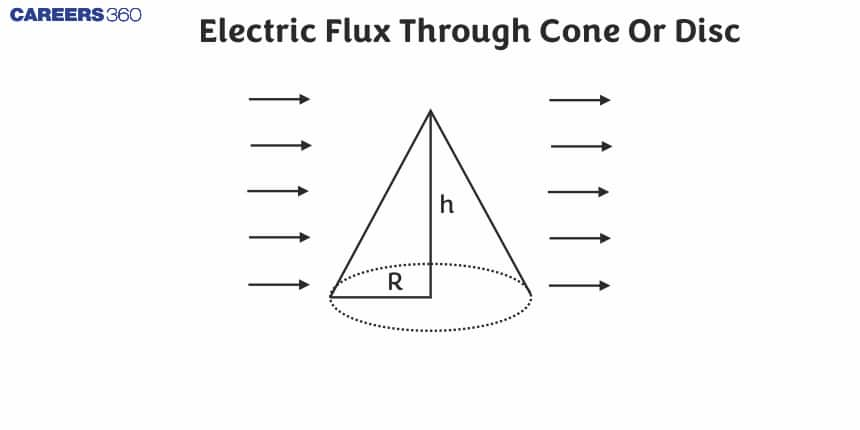
When considering surfaces like a cone or a disc, the electric flux through them depends on the shape of the surface and its orientation relative to the electric field. For a cone, the flux might vary depending on the angle of the cone relative to the field, while for a disc, it depends on whether the disc is perpendicular or at an angle to the field lines. Understanding this concept is essential in many areas of physics, particularly in applying Gauss’s Law, which helps simplify complex electric field calculations. In this article, we'll delve into how electric flux is calculated through a cone or disc and explore some practical examples to help illustrate the concept.
The electric flux through a cone or disc
There are several cases for electric flux calculation. In this concept, we will discuss one very important and complex case which is ''Electric flux through cone or disc''. For this let us consider a point charge at a distance 'a' from a disc of radius R as shown in the given figure.

Let us consider an elemental ring of radius "
Electric field due to
If
To obtain total flux, we should integrate this expression over the whole area of the ring, So the total flux can be given as
On integration we get,
Recommended Topic Video
Solved Examples Based on Electric flux through Cone or Disc
Example 1: A cylinder of radius
1)
2)
3)
4) zero
Solution:
Electric field E through any area A
wherein
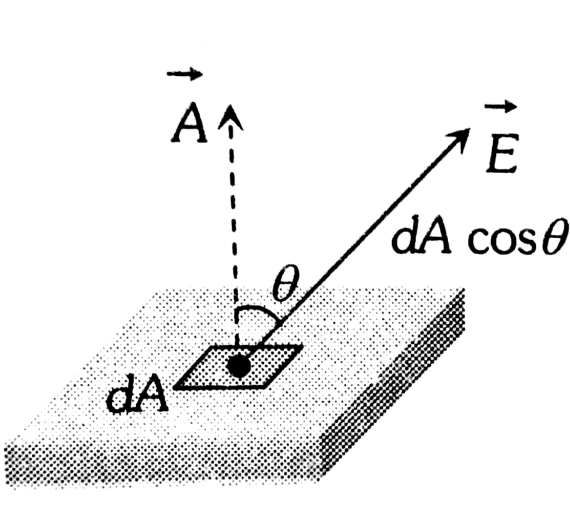
Flux through surface
Flux through curved surface
Total flux through cylinder
Hence, the answer is option (4).
Example 2: The Electric field at a point varies as
1) An electric dipole
2) A point charge
3) A plane infinite sheet of charge
4) A line charge of infinite length
Solution:
Electric field E through any area A
wherein

Hence, the answer is option (3).
Example 3: Shown in the figure are two point charges

Solution:
if the Electric field is variable
Inside the cavity, the net charge is zero
There is no effect of point charge and induced charge on the inner surface and the outer surface
Example 4: If the electric flux entering and leaving an enclosed surface respectively is
1)
2)
3)
4)
Solution:
if the Electric field is variable
Hence, the answer is the option (2).
Example 5: The inward and outward electric flux for a closed surface in units of
1)
2)
3)
4)
Solution:
if the Electric field is variable
By Gauss's law
Hence, the answer is the option (4).
Summary
The electric flux through a surface is a measure of the electric field passing through that surface. For a cone or disc, this may be represented by pondering on the number of electric field lines that pierce such shapes. When a uniform electric field is at right angles to the base of a cone or disk, the product of the electric field intensity and the area of the base gives the value of flux.
Frequently Asked Questions (FAQs)
