Electrostatic Potential and Capacitance
Electrostatic potential and capacitance are important concepts in physics that deal with electric charges and their behavior. Electrostatic potential explains the work done in bringing a unit charge from infinity to a point in an electric field, while capacitance tells us how much charge a conductor can store per unit potential. These concepts are widely applied in real life, from capacitors in electronic devices to the working of touchscreens. In class 12 studying electrostatic potential and capacitance builds a foundation for understanding electric fields, energy storage, and many applications in electronics and technology.

Electrostatic Potential and Capacitance Class 12 Topics (NCERT Syllabus)
Electrostatics, Potential and Capacitance in Class 12 is a core part of Physics and forms the basis for understanding electric charges and fields. It is one of the most important chapters for board exams as well as competitive exams like JEE and NEET. This chapter builds the foundation for topics in electricity, electronics, and modern physics, making it essential for mastering advanced concepts.
1. Introduction
Energy is a conserved quantity and helps solve problems in mechanics without always using Newton’s laws. The same idea applies to electricity, where energy provides an easier way to study electrical phenomena. Electric energy can be stored in a capacitor, a common device in almost all circuits. Capacitors act like energy storage units, for example, in camera flashes where stored energy is released quickly to produce a bright flash.
2. Electrostatic Potential
Electrostatic potential at a point is the work done per unit charge in bringing a small positive test charge from infinity to that point, without acceleration.
$
V=\frac{W}{q}
$
3. Potential Due to a Point Charge
Consider a point charge $q$ placed at point $O$. Consider any point $P$ in the field of the above charge. Let us calculate the potential at point $P$ due to the charge $q$ kept a point $O$.
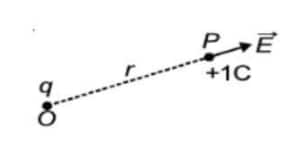
Let the distance $O P=r$.
Let $\overrightarrow{O P}=\vec{r}$.
The field at $P$, due to $q$ will be directed along $\overrightarrow{O P}$, given by
$
E=\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2} \text { or } \vec{E}=\frac{1}{4 \pi \varepsilon_0} \frac{q}{r^2} \hat{r}
$
4. Potential Due to An Electric Dipole
An electric dipole consists of two equal and opposite charges ( $+q$ and $-q$ ) separated by a small distance $2 a$.
The electrostatic potential at a point $P$ (at distance $r$ from the center of dipole, making angle $\theta$ with dipole axis) is:
$
V=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{p \cos \theta}{r^2}
$
5. Potential Due to a System of Charges
The electrostatic potential at a point due to a group of charges is the algebraic sum of potentials due to each charge.
For charges $q_1, q_2, q_3, \ldots q_n$ located at distances $r_1, r_2, r_3, \ldots r_n$ from a point $P$,
$
V=\frac{1}{4 \pi \varepsilon_0}\left(\frac{q_1}{r_1}+\frac{q_2}{r_2}+\frac{q_3}{r_3}+\cdots+\frac{q_n}{r_n}\right)
$
6.Equipotential Surfaces
An equipotential surface is a surface with a constant value of potential at all points on the surface. For a single charge $q$, the potential is given by :
$
V=\frac{1}{4 \pi \varepsilon_o} \frac{q}{r}
$
This shows that $V$ is a constant if $r$ is constant. Thus, equipotential surfaces of a single point charge are concentric spherical surfaces centred at the charge.
7. Potential Energy Of A System Of Charges
The potential energy of a system of charges is the work done in assembling the charges from infinity to their given positions in space.
For two point charges $q_1$ and $q_2$ separated by distance $r$ :
$
U=\frac{1}{4 \pi \varepsilon_0} \cdot \frac{q_1 q_2}{r}
$
8. Potential Energy in an External Field
When a charge is placed in an external electric field, it possesses potential energy due to its position.
For a single charge $q$ at potential $V$ :
$
U=q V
$
For a system of charges $q_1, q_2, \ldots q_n$ in an external potential $V$ :
$
U=q_1 V_1+q_2 V_2+\cdots+q_n V_n
$
9. Electrostatics of Conductors
- Inside a conductor, electrostatic field is zero
- At the surface of a charged conductor, electrostatic field must be normal to the surface at every point
- The interior of a conductor can have no excess charge in the static situation
- Electrostatic potential is constant throughout the volume of the conductor and has the same value (as inside) on its surface
-
Electric field at the surface of a charged conductor
$
\mathbf{E}=\frac{\sigma}{\varepsilon_0} \hat{\mathbf{n}}
$
10. Dielectrics and Polarisation
- Dielectrics are non-conducting materials (like glass, plastic, mica, ceramic) that do not allow free flow of charges.
- Instead, they can be polarised when placed in an electric field.
Polarisation of Dielectrics
When an external electric field is applied, positive and negative charges inside a dielectric shift slightly in opposite directions.This creates tiny dipoles inside the material the process is called polarisation.
11. Capacitors and Capacitance
- A capacitor is a device that stores electric charge and energy.
- It consists of two parallel conducting plates separated by a gap (air or dielectric).
Capacitance (C):
The ability of a capacitor to store charge. $C=\frac{Q}{V}$
12. The Parallel Plate Capacitor
A parallel plate capacitor consists of two large conducting plates placed parallel to each other and separated by a small distance.
$C=\frac{\varepsilon_0 A}{d}$
13. Effect of Dielectric on Capacitance
Without dielectric:
For a parallel plate capacitor,
$
C=\frac{\varepsilon_0 A}{d}
$
With dielectric:
When a dielectric material of dielectric constant $\mathbf{K}$ is inserted between the plates, the capacitance increases:
$
C=\frac{K \varepsilon_0 A}{d}
$
14. Combination of Capacitors
Series Combination
In series, the reciprocal of total capacitance is the sum of reciprocals:
$
\frac{1}{C_{\mathrm{eq}}}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}+\ldots
$
Parallel Combination
In parallel, total capacitance is the sum of all capacitances:
$
C_{\mathrm{eq}}=C_1+C_2+C_3+\ldots
$
15. Energy Stored in a Capacitor
When a capacitor is charged, it stores energy in the form of an electric field between its plates.
The energy stored is:
$
U=\frac{1}{2} C V^2
$
Related Topics,
Electrostatic Potential and Capacitance Real Life Examples
Electrostatic Potential Examples
- Lightning: A natural example where charges build up in clouds, creating a huge potential difference with the ground.
- Van de Graaff Generator: Creates high potential to study electrostatics in labs.
- Xerox Machines & Laser Printers: Use electrostatic potential to attract toner particles onto paper.
Capacitance Examples
- Camera Flash: Capacitors store energy and release it quickly to produce a bright flash.
- Defibrillators: Use capacitors to store charge and deliver a sudden shock to restart the heart.
- Touchscreens: Capacitive touchscreens sense the change in capacitance when you touch them.
- Fans & Motors: Capacitors are used to start and run electric motors in household appliances.
Exam-wise Weightage of Electrostatic Potential and Capacitance
| Exam | Approximate Weightage | Remarks |
|---|---|---|
| NEET | 2 - 4% | Important for basics of electrostatics; simple numericals asked. |
| Board | 5% | Frequently comes as derivations, definitions, and short numericals. |
| JEE | 2 - 4% | Conceptual + numerical questions; applications of capacitor formulas are common. |
Importance of Electrostatic potential and capacitor class 12:
Class 12 chapter 2 electrostatic potential and capacitance gives a thorough understanding of the subject, as well as possible responses to the most often asked questions Furthermore, the full explanations for each subject and subsection are provided in plain language, allowing students to ace their tests with a well-rounded understanding. Class 12 chapter 2 electrostatic potential and capacitance is a major topic of board exam and along with this it is a crucial part of joint entrance exam (jee) and national entrance and National Eligibility cum Entrance Test (neet ).To do well in the category 12 board test, students must be comprehensive with their studies. Students must plan well and practise with NCERT Class 12 Chapter two Electrostatic potential and capacitor Physics Marks Wise Question in order to achieve excellent grades in class 12.
Approach to Solve Electrostatic Potential and Capacitance Questions
When solving electrostatic potential and capacitance problems, first check if the question is about potential capacitance or energy. Draw the diagram and write the known values. Use the correct formula - for example, $V=\frac{W}{q}, C=\frac{Q}{V}$, or $U=\frac{1}{2} C V^2$. In case of multiple charges add their potentials (since potentials are scalars). For capacitor combinations, apply series or parallel formulas carefully. Always check the final unit ( $\mathrm{V}, \mathrm{F}$, or J ) before writing the answer.
- NCERT solutions for class 12 Electrostatic potential and capacitor.
- NCERT exemplar solutions for class 12 physics chapter 2 Electrostatic potential and capacitor
- NCERT notes for class 12 physics chapter 2 Electrostatic potential and capacitor
NCERT Solutions Subject wise link:
- NCERT solutions for class 12 Physics.
- NCERT solutions for class 12 Chemistry.
- NCERT solutions for class 12 Mathematics.
- NCERT solutions for class 12 Biology.
NCERT Exemplar Solutions Subject wise link:
- NCERT exemplar solutions for class 12 Physics.
- NCERT exemplar solutions for class 12 Chemistry.
- NCERT exemplar solutions for class 12 Mathematics.
- NCERT exemplar solutions for class 12 Biology.
NCERT Notes Subject wise link:
Frequently Asked Questions (FAQs)
Around eight to ten marks, questions are asked there is variance because of the different patterns so around 10 to 15 percentage questions are asked about Electrostatic potential and capacitor.
In the NEET exam, an average of one question, with a weightage of roughly two percentage, is asked. Electrostatic potential and capacitor
As Mentioned in the Class 12 Physics Chapter 2 Electrostatic potential and capacitor there are three types of charging,
i) by friction
ii) by electrostatic induction
iii) charging by conduction
There are three types of capacitors based on their shape
i) Parallel Plate Capacitors
ii) Spherical Capacitors,
iii) Cylindrical capacitors
Class 12 Physics, Chapter 2 - Electrostatic Potential and Capacitance, has a number of real-world applications. Many technologies and equipment would be obsolete if Electrostatistics was not studied. Electrostatics are used in the Van de Graaff Generator and Xerography (Photocopy Machines). Electrostatic ideas are also used in Laser Printers and Inkjet Printers. Electrostatic Painting, Smoke Precipitators, and Electrostatic Air Cleaning are some more examples. Electrostatics and related principles control our daily lives and aid in the simplification of our duties.