Gravitational Potential

Definition of Gravitational Potential

The gravitational point at any point is defined as the negative of work done by the gravitational force in moving a unit test mass from infinity (where the potential is assumed to be zero) to that point Thus, the potential at P is $V_p=\frac{-W_{\infty \rightarrow P}}{m}$ (by gravitational force). it is a Scalar Quantity.

Unit $\rightarrow$ Joule $/ \mathrm{kg}$ or $\mathrm{m}^2 / \mathrm{sec}^2$
Dimension : $\left[M^0 L^2 T^{-2}\right]$

Gravitational Potential Due to Uniform Circular Ring

A uniform circular ring is a symmetrical distribution of mass, where each element of the ring exerts a gravitational pull on a point in space. The gravitational potential at a point along the axis of the ring depends on the distance from the centre of the ring and the ring’s radius.

For Uniform circular ring

$r=$ distance from ring
$a \rightarrow$ radius of Ring
$V \rightarrow$ Potential

At a point on its Axis

$
V=-\frac{G M}{\sqrt{a^2+r^2}}
$
At the centre

$
V=-\frac{G M}{a}
$

Solved Examples Based on Gravitational Potential

Example 1: The dimensional Formula of Gravitational Potential is

1) $\left[M L^2 T^{-1}\right]$
2) $\left[M^0 L^2 T^{-3}\right]$
3) $\left[M L^2 T^{-2}\right]$
4) $\left[M^0 L^2 T^{-2}\right]$

Solution:

Gravitational Potential

Scalar Quantity is defined as work done per unit of mass

Unit $\rightarrow$ Joule $/ \mathrm{kg}$ or $\mathrm{m}^2 / \mathrm{sec}^2$
Dimension : $\left[M^0 L^2 T^{-2}\right]$
wherein

$
\begin{aligned}
V & =-\frac{W}{m}=-\int \frac{\vec{F} \cdot \overrightarrow{d r}}{m} \\
V & =-\int \vec{I} \cdot \overrightarrow{d r}
\end{aligned}
$

$V \rightarrow$ Gravitational potential
$I \rightarrow$ Field Intensity
$d r \rightarrow$ small distance
As

$
\begin{aligned}
& V=\frac{-G M}{r} \\
& {[V]=\frac{[G][M]}{[r]}=\frac{\left[M^{-1} L^3 T^{-2}\right] \cdot[M]}{[L]}=\left[M^0 L^2 T^{-2}\right]}
\end{aligned}
$

Hence, the answer is the option (4).

Example 2: In a certain region of space, the gravitational field is given by $I=-\left(\frac{K}{R}\right)$ Taking the reference point to be at $r=r_0$ and potential at the reference point as $V=V_0$. Then find the potential at a general point.

1) $K \log \left(\frac{r}{r_0}\right)+V_0$
2) $K \log \left(\frac{r_0}{r}\right)+V_0$
3) $K \log \left(\frac{r}{r_0}\right)-V_0$
4) $K \log \left(\frac{r_0}{r}\right)-V_0$

Solution:

$\begin{aligned} & I=\frac{-d v}{d r} \text { or } d v=-I d r \\ & \int_{v_0}^v d v=-\int_{r_0}^r\left(\frac{-k}{r}\right) d r \\ & {[V]_{v o}^v=K[\log r]_{r o}^r=K\left[\log r-\log r_o\right]} \\ & V-V_0=K \log \frac{r}{r_o} \Rightarrow V=K \log \frac{r}{r_0}+V_o\end{aligned}$

Hence, the answer is the option (1).

Example 3: In the following figure potential difference $V_B-V_A$ is equal to

1) $-G M\left[\frac{1}{r_1}-\frac{1}{r_2}\right]$
2) $-G M\left[\frac{1}{r_2}-\frac{1}{r_1}\right]$
3) $G M\left[\frac{1}{r_2}+\frac{1}{r_1}\right]$
4) $-G M\left[\frac{1}{r_1}+\frac{1}{r_2}\right]$

Solution:

Gravitational Potential difference

$
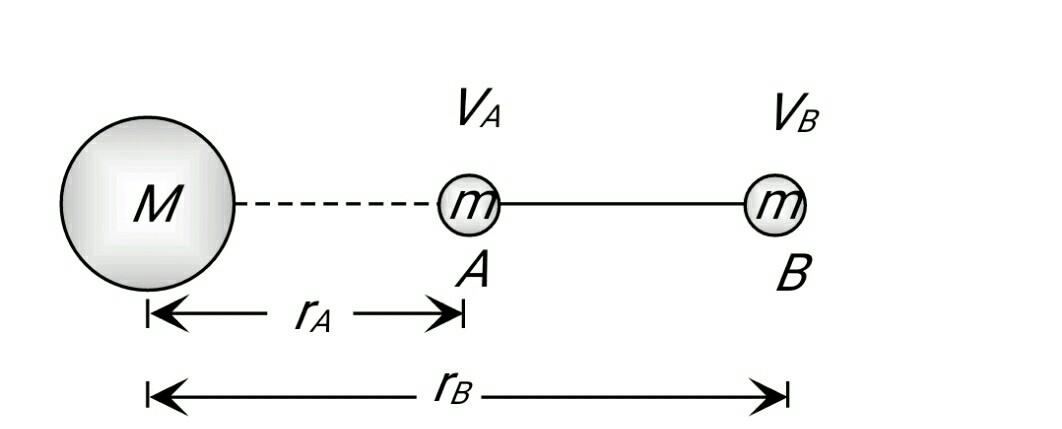
\begin{aligned}
& \Delta V=V_B-V_A=\frac{W_{A \rightarrow B}}{m} \\
& \Delta V=-G M\left[\frac{1}{r_B}-\frac{1}{r_A}\right]
\end{aligned}
$

wherein
$r_B \rightarrow$ the distance of mass at $B$
$r_A \rightarrow$ distance of mass at $A$

$
\begin{aligned}
& \Delta V=V_B-V_A=\frac{-G M}{r_2}-\left(\frac{-G M}{r_1}\right) \\
& =\frac{-G M}{r_2}-\frac{-G M}{r_1} \\
& V_B-V_A=-G M\left[\frac{1}{r_2}-\frac{1}{r_1}\right]
\end{aligned}
$

Hence, the answer is the option (2).

Example 4: Infinity number of the masses, each 1 kg, are placed along the X-axis at $x= \pm 1 m, \pm 2 m, \pm 4 m, \pm 8 m, \pm 16 m,-\cdots--\infty$. The magnitude of the resultant gravitational potential in terms of gravitational constant G at the origin is $n \times G$. Then 'n' will be :

1) 4

2) 2

3) 8

4) 0.5

Solution:

As we know $V=\frac{-G m}{r}$

$
|V|=\left|\frac{-G m}{r}\right|=\frac{G m}{r}
$
Total Potential ( v ) $=\frac{2 G m}{r}$ [because particle along both sides]

$
\begin{aligned}
& V=2 G m\left[1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\cdots-\cdots-\cdots \infty\right. \\
& =2 G m\left[\frac{1}{1-\frac{1}{2}}\right]\left[A s S_{\infty}=\frac{a}{1-r}\right] \\
& V=\frac{2 G m}{\frac{1}{2}}=4 G m
\end{aligned}
$
As, $m=1 \mathrm{~kg}$
So, $V=4 G$
Hence $n=4$

Hence, the answer is the option (1).

Summary

Gravitational potential is the potential energy per unit mass in a gravitational field, essential for understanding how objects interact within this field. The gravitational potential due to a uniform circular ring depends on the distance from the ring’s axis and its radius, with specific formulas for points on the axis and at the centre. Solved examples illustrate the dimensional formula, potential difference, and potential at specific points, demonstrating the application of gravitational potential in various scenarios.