Heat Transfer

Heat Transfer

Heat transfer is the movement of thermal energy from one object or substance to another due to a temperature difference. This process is essential in both natural and engineered systems, affecting everything from the weather patterns we experience to the design of heating and cooling systems in buildings. Heat transfer occurs through three primary mechanisms:

Conduction

This is the direct transfer of heat through a material, like when you touch a hot stove and feel the heat transfer to your hand. Metals are good conductors because heat moves easily through them.

Convection

This happens in fluids (liquids and gases) when warmer areas of a fluid rise and cooler areas sink, creating a cycle of heat movement. It’s how heat spreads in boiling water or why warm air rises in a room.

Radiation

This is heat transfer through electromagnetic waves, such as the warmth you feel from the sun on a clear day. No physical medium is required for radiation, making it different from conduction and convection.

Recommended Topic Video

Solved Examples Based on Heat Transfer

Example 1: The layer of the atmosphere is heated through

1) Convection

2) Conduction

3) Radiation

4) 2 & 3 both

Solution:

Natural Convection

This arises due to the difference of densities at two places.

wherein

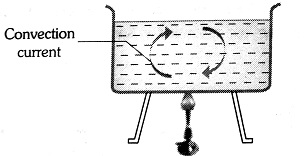
The heating of the atmosphere is mainly because of natural convection.

Hence, the answer is option (1).

Example 2: Heating of a room using a blower is an example of

1) Conduction

2) Natural convection

3) Forced convection

4) Radiation

Solution:

Forced Convection

If a fluid is forced to move to take up heat from a hot body.

wherein

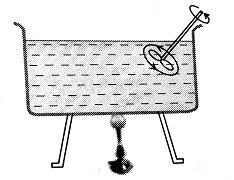
So, heat transfer with the help of a blower is an example of heat transfer through forced convection.

Hence, the answer is option (3).

Example 3: The height of Victoria Falls is $63 \mathrm{~m}$. What is the difference in temperature of water at the top and at the bottom of the fall?
$
\left[\text { Given } 1 \mathrm{cal}=4.2 \mathrm{~J} \text { and specific heat of water }=1 \mathrm{calg}^{-1 \circ} \mathrm{C}-1\right]
$

1) $1.476^{\circ} \mathrm{C}$
2) $14.76^{\circ} \mathrm{C}$
3) $0.147^{\circ} \mathrm{C}$
4) $0.014^{\circ} \mathrm{C}$

Solution:

As the water falls, all of it PE will continue into heat as it hits the bottom

$\begin{aligned} & m g h=m c \Delta T \\ & 10 \times 63=\frac{4.2 J}{10^{-3} \mathrm{~kg}{ }^0 \mathrm{C}} \times \Delta T \\ & \Delta T=\frac{630}{4.2}=\frac{6300}{42}=900 \times 10^{-3} \\ & \Delta T=150 \times 10^{-3} \\ & \Delta T \cong 0.15\end{aligned}$

Hence, the answer is option (3).

Example 4: If 5mg of a liquid at temperature T and specific heat 2s is mixed with 5mg of another liquid with temperature 2T and specific heat 3s then the final temperature of the mixture is

1) $\frac{2 T}{3}$
2) $\frac{8 T}{3}$
3) $\frac{8 T}{5}$
4) $\frac{3 C}{2}$

Solution:

If $m_1=m_2$

$
\theta_{m i x}=\frac{\theta_1 c_1+\theta_2 c_2}{c_1+c_2}
$

wherein
If bodies are of the same mass.

$
\begin{aligned}
& T^{m i x}=\frac{s_1 \theta_1+s_2 \theta_2}{s_1+s_2} \\
= & \frac{2 s T+3 s \cdot 2 T}{5 s} \\
= & \frac{8 T}{5}
\end{aligned}
$

Hence, the answer is option (3).

Example 5: The rate of radiation of the black body is E J/sec. The rate of radiation (in E) of this black body at 273^oC will be :

1)16

2)8

3)4

4)1

Solution:

$
\begin{gathered}
E \propto \theta^4 \\
\Rightarrow E=\sigma \theta^4 \\
\frac{E_2}{E_1}=\left(\frac{T_2}{T_1}\right)^4
\end{gathered}
$
Where T is the Temperature in kelvin

$
\Rightarrow\left(\frac{273+273}{273+0}\right)^4=16
$

Hence, the answer is option (1).

Summary

Heat transfer is the process of how heat transfers from the hot object to the cold one. There are three ways of this happening: conduction, convection, and radiation. Conduction is when heat transfers through direct touch, convection is where heat is transferred through liquids or gases, and radiation is where heat is transferred in waves through space. Learning these routes helps us control heat in things like heaters, coolers, and so many other tools and gadgets.