Hooke’s Law Equation Experiment - Definition, FAQs

What is Hooke's Law

Hooke's law definition: This law states that the strain is proportional to stress applied to the material within the elastic limit. Hooke's Law is regarded as one of the finest physics principles.

In the 17th century, British physicist Robert Hooke developed. He established a link between the numerous forces applied to a spring and its elasticity.

Related Topics,

• Stress-Strain Relationship
• Relation Between Volumetric Strain, Lateral Strain, And Poisson’s Ratio
• Work Done In Stretching A Wire

Hooke's Law Experiment

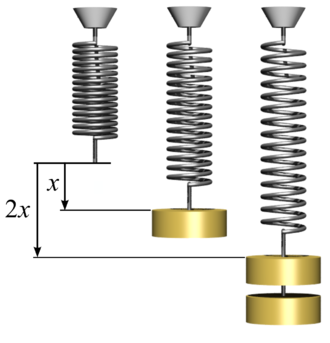
The experiment aims to find the spring constant using Hooke's law

The procedures included in the experiment are:

Attach the spring vertically to a stand and measure the initial length of the spring. Now attach a known weight to the spring and measure the length which is extended. Repeat the process for different weights and mark down the length measurement. Plot a graph with applied force on the y-axis and extension on the x-axis. The slope of this graph represents the spring constant.

Hooke’s Law Formula

$$
F_S=-k x
$$

where,

• $F_S$ is the restoring force exerted by the spring
• $k$ is the spring constant
• $x$ is the displacement of the spring from its equilibrium position

Hooke's law is applicable within the spring's valid elastic limit. The only attribute that allows the spring to remain in a limited space is its elasticity. The spring will lose its property if it breaks.

Hooke's Law, on the other hand, only works in a narrow context. This is analogous to the most fundamental law of mechanics. This is because no material can be crushed or stretched beyond a specific minimum or maximum size.

State Hooke's Law of Elasticity

There is no way to permanently distort or modify the state of the spring. Hooke's law is only relevant when a small amount of force or deformation is involved. Consider the fact that many materials will diverge dramatically from Hooke's law. This is due to their extremely pliable boundaries.

Some general types of physics can relate Hooke's Law to Newton's rules of static equilibrium since they are mutually compatible. When stress and strain are evaluated simultaneously, the accurate relationship between strain and stress for complicated objects may be traced.

This relationship is entirely dependent on the intrinsic qualities of materials. Consider the case of a homogeneous rod with a uniform cross-section. During the stretching, this rod will function as a basic spring.

The stiffness (k) of the rod is related to the area of the rod's cross-section. Too, according to the law of elasticity, it is inversely proportional to its length.

Application of Hooke's Law

1. They measure weight in devices like luggage scales and weighing machines.
2. Used in braces to align teeth
3. Used in trampoline
4. Used to determine the elastic properties of materials
5. Used in musical instruments like guitar and violin
6. Used in beds and mattresses to provide support and comfy

Explain the Stress-Strain Diagram

Hooke's law graph, also known as stress-strain, shows the relationship between the stress of a material and the resulting strain. The mechanical properties of a material can be determined by illustrating Hooke's law graph.

The key characteristics of Hooke's law graph are:

Proportional limit: This region follows Hooke's law that is, stress is directly proportional to strain.

• Elastic limit: Hooke's law is not applicable in this region but material can regain its original shape.
• Yield Point: It's the end of the elastic region. The material cannot return to its original shape and is permanently deformed even after the stress is removed.
• Plastic Region: The material undergoes permanent deformation and the stress increases nonlinearly with strain.
• Ultimate Stress Point: If a material goes beyond this region, it starts to weaken. This is the region in which a material can withstand the maximum stress.
• Fracture point: Material breaks in this region.

Disadvantages Of Hooke's Law

1. Hooke's law is applicable only within the elastic limit.
2. It does not apply to non-linear materials like rubber and polymers.
3. The law depends on temperature.

What is Elastic Limit

The elastic limit is the maximum stress that can be applied to a material without getting permanently deformed. When the force is removed the material goes back to its original shape and Hooke's law is also applicable. Beyond the elastic limit, the material will be deformed and does not return to its original shape.

Also read:

• NCERT Exemplar Solutions for All Subjects
• NCERT Notes For All Subjects
• NCERT Solutions for All Subjects

Recommended Topic Video

Solved Examples Based on Hooke's law

Example 1: Hooke's law essentially defines

1) stress

2) strain

3) yield point

4) elastic limit

Solution

Hooke's Law

stress $\propto$ strain

stress strain =$E$

wherein

$E$= modulus of elasticity

Hence, the answer is the option (4).

Example 2: A uniformly tapering conical wire is made from a material of Young’s modulus Y and has a normal, unextended length L. The radii, at the upper and lower ends of this conical wire, have values R and 3R, respectively. The upper end of the wire is fixed to a rigid support and a mass M is suspended from its lower end. The equilibrium extended length, of this wire, would equal

1. $L\left(1+\frac{29 M g}{\pi Y R^2}\right)$
2. $L\left(1+\frac{13 M g}{\pi Y R^2}\right)$
3. $L\left(1+\frac{19 M g}{\pi Y R^2}\right)$
4. $L\left(1+\frac{23 M g}{\pi Y R^2}\right)$

Solution:

Young Modulus

The ratio of normal stress to longitudinal strain

it denoted by Y
Y= Normal stress longitudinal strain

wherein

$$
Y=\frac{F / A}{\Delta l / L}
$$

Where:

• F: Applied force
• $A$ : Area
• $\Delta l$ : Change in length
• $L$ : Original length

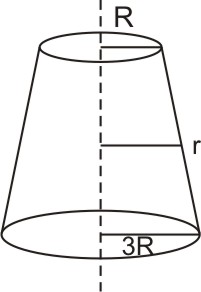
$\begin{gathered}r-R x=3 R-R L \quad \Rightarrow \quad r=R\left(1+2 \frac{x}{L}\right) \\ Y=\frac{m g}{\pi R^2} \cdot \frac{d L}{d x} \Rightarrow \quad d L=\frac{m g}{\pi R^2} \cdot \frac{d x}{\left(1+2 \frac{x}{L}\right)^2} \\ \Delta L=\frac{m g L}{Y \pi R^2} \int_0^L \frac{d x}{\left(1+2 \frac{x}{L}\right)^2} \quad \Rightarrow \quad \Delta L=\frac{m g L}{Y \pi R^2} \cdot \frac{1}{1+2 \frac{x}{L}} \\ L^{\prime}=L+\Delta L=L\left(1+\frac{13 m g}{\pi R^2 Y}\right)\end{gathered}$

Hence, the answer is the option (2).

Example 3: A wire elongates by l mm when a load W is hung from it. If the wire goes over a pulley and two weights W each are hung at the two ends, the elongation of the wire will be (in mm )

1) l/2
2) l
3) 2 L
4) zero

Solution:

Young Modulus

The ratio of normal stress to longitudinal strain

it denoted by Y
Y= Normal stress longitudinal strain

wherein

$$
Y=\frac{F / A}{\Delta l / L}
$$

Where:

• F: Applied force
• $A$ : Area
• $\Delta l$ : Change in length
• $L$ : Original length

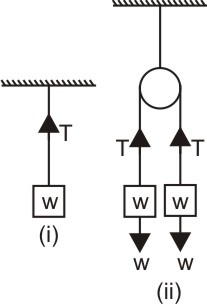
At equilibrium $T=W$ :

$$
Y=\frac{W / A}{\Delta l / L}
$$
Now, in case (ii), $T=W$ :
Let the new elongation be $\Delta l$.

$$
Y=\frac{W}{A} \cdot \frac{L}{\Delta l}
$$
So,

$$
\Delta l=\frac{W L}{A Y}
$$

i.e. Elongation is the same.

Hence, the answer is the option (2).

Example 4: A sonometer wire of length 1.5 m is made of steel. The tension in it produces an elastic strain of 1%. What is the fundamental frequency (in Hz ) of steel if the density and elasticity of steel are $7.7 \times 103 \mathrm{~kg} / \mathrm{m}^3$ and $2.2 \times 1011 \mathrm{~N} / \mathrm{m}^2$ respectively?

1) 770

2) 188.5

3) 178.2

4) 200.5

Solution:

Young Modulus

The ratio of normal stress to longitudinal strain

$$
Y=\frac{F / A}{\Delta l / L}
$$
Where:
- F: Applied force
- $A$ : Area
- $\Delta l$ : Change in length
- $L$ : Original length

Fundamental frequency:

$$
\begin{gathered}
v=\frac{1}{2 L} \cdot \sqrt{\frac{T}{\mu}}=\frac{1}{2 L} \sqrt{\frac{T}{\rho A}} \\
\rho=\frac{1}{2} \times 1.5 Y \times \text { strain }=\frac{1}{3} \cdot 2.2 \times 10^{11} \cdot 10^{-27.7 \times 10^3}=178.2 \mathrm{~Hz}
\end{gathered}
$$
Hence, the answer is the option (3).

Example 5: Young's moduli of two wires A and B are in the ratio 7:4. Wire A is 2 m long and has a radius of R. Wire B is 1.5 m long and has a radius of 2 mm. If the two wires stretch by the same length for a given load, then the value of R (in mm) is close to:

1) 1.5

2) 1.9

3) 1.7

4) 1.3

Solution:

$\begin{aligned} Y & =\frac{F}{A} \cdot \frac{\Delta l}{L} \\ Y & =\frac{F L}{\pi r_A^2 \Delta l_A} \times \frac{\pi r_B^2 \Delta l_B}{F L_B} \\ 74 & =2 \times\left(r_A\right)^2 \times 22 \times 1.5 \\ r_A^2 & =4 \times 2 \times 22 \times 1.5 \times 7 \\ r_A & =1.7 \mathrm{~mm}\end{aligned}$

Hence, the answer is the option (3).