Moment Of Inertia Of A Solid Sphere

A solid sphere is a type of sphere that possesses material in the form of its core inside the wall. The centre of a solid sphere is the same as the hollow sphere; the only difference is the prominent availability of the material of the sphere. The inability of a body to change its state of rest or of uniform linear motion by itself is known as inertia. A body rotating about an axis is unable to produce a change in its rotational motion by itself and this inertness in the case of rotational motion is known as rotational inertia.

This Story also Contains

1. Moment of Inertia of a Solid Sphere
2. Solved Examples Based on Moment of Inertia of a Solid Sphere
3. Summary

In this article, we will cover the concept of a solid sphere. This topic falls under the broader category of rotational motion, which is a crucial chapter in Class 11 physics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination (JEE Main), National Eligibility Entrance Test (NEET), and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE and more. Over the last ten years of the JEE Main exam (from 2013 to 2023), almost nine questions have been asked on this concept. And for NEET one questions were asked from this concept.

Let's read this entire article to gain an in-depth understanding of the moment of inertia of a solid sphere

Moment of Inertia of a Solid Sphere

Let I = Moment of inertia of a solid sphere about an axis through its centre

To calculate I

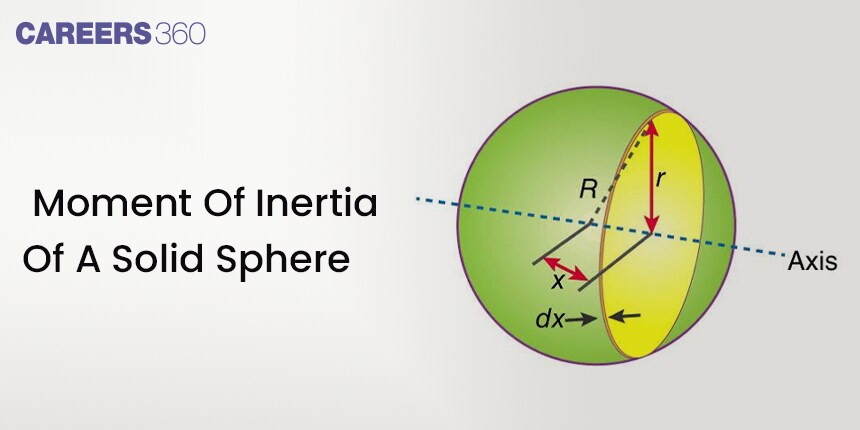
Consider a sphere of mass M, radius R and centre O. Mass per unit volume of the sphere = $\rho=\frac{M}{\frac{4}{3} \pi R^3}$

Take an elementary disc of mass dm, whose centre is C and which lies between two planes perpendicular to the axis at a distance x and x + dx from its centre

Disc has Radius=AC and thickness =dx.

As shown in the figure

So, $A C=\sqrt{R^2-x^2}$
So, $d V=\pi\left(R^2-x^2\right) d x$
$
d m=\rho d V=\frac{3 M}{4 \pi R^3} * \pi\left(R^2-x^2\right) d x=\frac{3 M}{4 R^3} *\left(R^2-x^2\right) d x
$

The moment of inertia of the elementary disc about the axis:

$d I=\int \frac{(A C)^2 d m}{2} \quad\left(\because I_{\text {disc }}=\frac{m R^2}{2}\right)$

Now integrate this dI between the limits x=-R to x=+R

$\begin{aligned}
& I=\int d I=\int \frac{(A C)^2 d m}{2} \\
& =\int_{-R}^R\left(R^2-x^2\right) \frac{3 M}{8 R^3}\left(R^2-x^2\right) d x \\
& =\int_{-R}^R \frac{3 M}{8 R^3}\left(R^2-x^2\right)^2 d x \\
& =\frac{3 M}{8 R^3} \int_{-R}^R\left(R^4-2 R^2 x^2+x^4\right) d x \\
& \Rightarrow \mathbf{I}=\frac{2}{5} \mathrm{MR}^2
\end{aligned}$

Recommended Topic Video

Solved Examples Based on Moment of Inertia of a Solid Sphere

Example 1: Two identical spherical balls of mass M and radius R each are stuck on two ends of a rod of length 2R and mass M (see figure) The moment of inertia (MR²) of the system about the axis passing perpendicularly through the centre of the rod is :

1) 10.13

2) 9.13

3) 13.93

4) 1.13

Solution:

Moment of inertia for a solid sphere

$
I=\frac{2}{5} M R^2
$

About a diameter.
$
\begin{aligned}
I_{\text {ball }} & =\frac{2}{5} M R^2+M(2 R)^2 \\
& =\frac{22}{5} M R^2
\end{aligned}
$
2 balls are there
$
\begin{aligned}
& \therefore \frac{44}{5} M R^2=I_{\text {balls }} \\
& I_{\text {rod }}=\frac{M(2 R)^2}{12}
\end{aligned}
$
$
\begin{aligned}
\mathrm{I}_{\text {system }} & =\mathrm{I}_{\text {balls }}+\mathrm{I}_{\text {rod }} \\
& =\frac{137}{15} M R^2
\end{aligned}
$

Hence, the answer is the option (2).

Example 2: Three solid spheres each of mass $\mathrm{m}$ and diameter $\mathrm{d}$ are stuck together such that the lines connecting the centres form an equilateral triangle of the side of length d. The ratio $\frac{I_O}{I_A}$ of the moment of inertia $\mathrm{I}_0$ of the system about an axis passing the centroid and about the centre of any of spheres $\mathrm{I}_{\mathrm{A}}$ and perpendicular to the plane of the triangle is:

1) $\frac{15}{13}$
2) $\frac{13}{15}$
3) $\frac{13}{23}$
4) $\frac{23}{13}$

Solution:

As a moment of inertia of one sphere of radius R about its $centre= I=\frac{2}{5} m R^2$

From the figure given it is clear that $O C=\frac{d}{\sqrt{3}}$

$\text { M.I about O }=3\left[\left(\frac{2}{5} M\left(\frac{d}{2}\right)^2+M\left(\frac{d}{\sqrt{3}}\right)^2\right)\right]=\frac{13}{10} M d^2$

$\text { M.I about A }=2\left[\left(\frac{2}{5} M\left(\frac{d}{2}\right)^2+M(d)^2\right)\right]+\frac{2}{5} M\left(\frac{d}{2}\right)^2=\frac{23}{10} M d^2$

$\text { New Ratio }=\frac{13}{23}$

Hence, the answer is option (3).

Example 3: One solid sphere A and another hollow sphere B are of the same mass and the same outer radii. Their moment of inertia about their diameters are respectively $I_A$ and $I_B$ such that:

$\text { Where } d_A \text { and } d_B \text { are their densities }$

1) $I_A=I_B$
2) $I_A>I_B$
3) $I_A<I_B$
4) $I_A / I_B=d_A / d_B$

Solution:

Solid sphere $I_s=\frac{2}{5} M R^2$
Hollow sphere $I_H=\frac{2}{3} M R^2$
$
\frac{I_s}{I_H}=\frac{3}{5}
$
i.e. $I_s<I_H$
$
\begin{aligned}
& I_s=I_A \\
& I_H=I_B
\end{aligned}
$
i.e. $I_A<I_B$

Hence, the answer is option (3).

Example 4: The moment of inertia (M.I.) of four bodies, having the same radius is reported as;
$I_1=$ M.l. of the thin circular ring about its diameter,
$I_2=$ M.I. of the circular disc about an axis perpendicular to the disc and going through the centre,
$I_3=$ M.i. of the solid cylinder about its axis and
$I_4=$ M.I. of the solid sphere about its diameter.

Then:

1) $I_1=I_2=I_3>I_4$
2) $I_1=I_2=I_3<I_4$
3) $I_1+I_3<I_2+I_4$
4) $I_1+I_2=I_3+\frac{5}{2} I_4$

Solution

Ring $\mathrm{I}_1=\frac{\mathrm{MR}^2}{2}$ about diameter

Disc $I_2=\frac{M R^2}{2}$
Solid cylinder $I_3=\frac{M R^2}{2}$
Solid sphere $\mathrm{I}_4=\frac{2}{5} \mathrm{MR}^2$
$
\mathrm{I}_1=\mathrm{I}_2=\mathrm{I}_3>\mathrm{I}_4
$

Hence, the answer is the option (1).

Example 5: The moment of Inertia (M.I) of four bodies having the same mass ${ }^{\prime} \mathrm{M}^{\prime}$ and radius ${ }^{\prime} 2 \mathrm{R}^{\prime}$ are as follows :
$\mathrm{I}_1=$ M.I of the solid sphere about its diameter.
$\mathrm{I}_2=$ M.I of the solid cylinder about its axis.
$\mathrm{I}_3=$ M.I of the solid circular disc about the diameter.
$\mathrm{I}_4=$ M.I of the thin circular ring about its diameter.
If $2\left(\mathrm{I}_2+\mathrm{I}_3\right)+\mathrm{I}_4=\mathrm{x} \cdot \mathrm{I}_1$, then the value of $\mathrm{x}$ will be $\qquad$

1) 5

2) 6

3) 7

4) 8

Solution:

$\begin{aligned}
& \mathrm{I}_1=\frac{2}{5} \mathrm{M}(2 \mathrm{R})^2=\frac{8 \mathrm{MR}^2}{5} \\
& \mathrm{I}_2=\frac{\mathrm{M}(2 \mathrm{R})^2}{2}=2 \mathrm{MR}^2 \\
& \mathrm{I}_3=\frac{\mathrm{M}(2 \mathrm{R})^2}{4}=\mathrm{MR}^2 \\
& \mathrm{I}_4=\frac{\mathrm{M}(2 \mathrm{R})^2}{2}=\frac{4 \mathrm{MR}^2}{2}=2 \mathrm{MR}^2 \\
& 2\left(\mathrm{I}_2+\mathrm{I}_3\right)+\mathrm{I}_4=\mathrm{xI}_1 \\
& 6 \mathrm{MR}^2+2 \mathrm{MR}^2=\mathrm{x} \frac{\left(8 \mathrm{MR}^2\right)}{5} \\
& 8 \mathrm{MR}^2=\mathrm{x} \frac{\left(8 \mathrm{MR}^2\right)}{5} \\
& \mathrm{x}=5
\end{aligned}$

Hence, the answer is option (1).

Summary

The moment of inertia of a solid sphere quantifies its resistance to rotational motion about an axis. This value depends on the sphere's mass and radius and is crucial for predicting the sphere's behaviour in rotational dynamics. Understanding this concept is essential for solving the example based on rotational motion.