Avogadro's Law: Definition, Formula, Equation, Examples, Questions

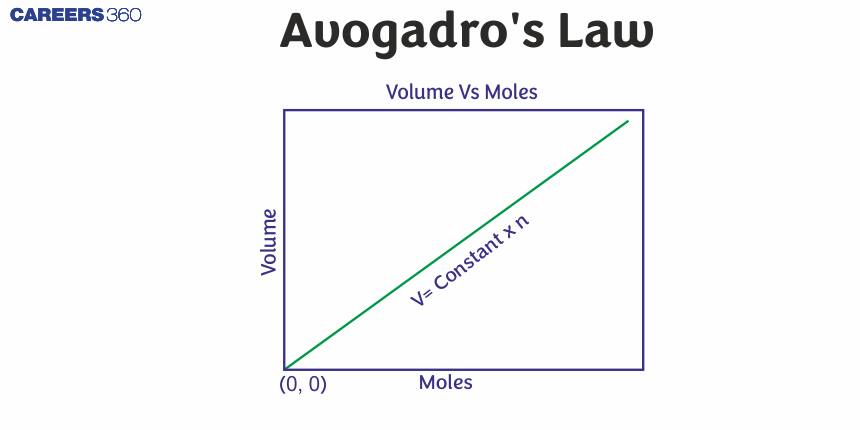
Avogadro’s Law

According to Avogadro's law, "At constant temperature and pressure, an equal volume of gases will have the same number of molecules or moles "

$
\begin{aligned}
& \mathrm{V} \propto \mathrm{N} \text { or } \mathrm{n} \\
& V / n=\text { constant } \\
& \frac{V_1}{N_1}=\frac{V_2}{N_2} \text { or } \frac{V_1}{n_1}=\frac{V_2}{n_2}
\end{aligned}
$

Here $\mathrm{n}=$ Number of moles of gas used
Here $\mathrm{N}=$ Number of molecules of gas used

Molar Volume or Gram Molecular Volume
1 mole of a gaseous substance has 22.4-litre volume at NTP which is known as its molar volume.

Avogadro Number
1 mole of a substance contains $6.02 \times 10^{23}$number of molecules.

1 gram atom of any element contains $6.02 \times 10^{23}$atoms,

Hence $\mathrm{N}_A=6.02 \times 10^{23}$

Recommended topic video on (Avogadro's Law )

Some Solved Examples

Example 1: If a mixture containing 3 moles of Hydrogen and 1 mole of Nitrogen is converted completely into Ammonia, the ratio of initial and final volume under the same temperature and pressure would be:

1)3 : 1

2)1 : 3

3) 2 : 1
4)1 : 2

Solution

N₂ + 3H₂ → 2NH₃
Initial = 1 3

final = – – 2

Total Initial moles = 4

Total final moles = 2

The ratio of moles = final/ initial

ratio $=\frac{4}{2}=\frac{2}{1}$

Avogadro’s Law -
Volume - mole relationship

$\begin{aligned} & \frac{V_1}{n_1}=\frac{V_2}{n_2} \\ & \frac{V_1}{V_2}=\frac{n_1}{n_2} \\ & \frac{V_1}{V_2}=\frac{4}{2}=\frac{2}{1}\end{aligned}$

Option (3) is correct.

Example 2: 50 g of nitrogen gas are contained in a 3 L container. The gas exerts a pressure of 3 atm on the container. If pressure is kept constant, what is the final molar amount of gas present in the container if gas is added until the volume has increased to 5 L ?

1)4

2) 3

3)2

4)5

Solution

We have given:
Mass of $N_2$ = 50g
Thus, moles of $N_2$ = 50/28 = 1.79 moles
Again, $V_i$ = 3 L and $V_f$ = 5L
Now, according to Avogadro’s law, we have:

$\begin{aligned} & \frac{V_i}{n_i}=\frac{V_f}{n_f} \\ & \frac{3}{1.79}=\frac{5}{n_f}\end{aligned}$

Thus, $n_f=3$ moles

Example 3: At 300 K, a sample of 3.0 g of gas A occupies the same volume as 0.2 g of hydrogen at 200 K at the same pressure. The molar mass of gas A is_____________g mol^-1. (nearest integer) Assume that the behavior of gases is ideal.

(Given: The molar mass of hydrogen (H₂) gas is 2.0 g mol^-1.)

1) 45

2)35

3)44

4)46

Solution

Let the molar mass of $\mathrm{A}=\mathrm{M}_{\mathrm{A}}$

Given, A and $\mathrm{H}_2$ occupy the same volume at the same pressure.

$\mathrm{V}_{\mathrm{A}}=\mathrm{V}_{\mathrm{H}_2}$

So, from the ideal gas equation, we have

$\begin{aligned} & \frac{\mathrm{n}_{\mathrm{A}} \mathrm{RT}_1}{\mathrm{P}}=\frac{\mathrm{n}_{\mathrm{H}_2} \mathrm{RT}_2}{\mathrm{P}} \\ & \Rightarrow 300 \times \mathrm{n}_{\mathrm{A}}=\mathrm{n}_{\mathrm{H}_2} \times 200 \\ & \Rightarrow 300 \times \frac{3.0 \mathrm{~g}}{\mathrm{M}_{\mathrm{A}}}=\frac{0.2 \mathrm{~g}}{2.0 \mathrm{~g} / \mathrm{mol}} \times 200 \\ & \Rightarrow \mathrm{M}_{\mathrm{A}}=30 \times \frac{3}{2} \mathrm{~g} / \mathrm{mol} \\ & \Rightarrow \mathrm{M}_{\mathrm{A}}=45 \mathrm{~g} / \mathrm{mol}\end{aligned}$

Hence, the answer is (45).

Example 4: A and B are two identical vessels. A contains 15g Ethane at 1atm and 298K. The vessel B contains 75g of a gas $X_2$ at same temperature and pressure. The vapour density of $X_2$ is :

1) 75

2)150

3)37.5

4)45

Solution

As we learnt in Avogadro’s Law that Volume - Mole relationship can be written as follows:

$\frac{V_1}{n_1}=\frac{V_2}{n_2}$

(Since $V_1$ and $V_2$ are equal as the vessels are identical)

$\begin{aligned} & \Rightarrow \frac{V}{n_1}=\frac{V}{n_2} \\ & \Rightarrow n_1=n_2 \\ & \Rightarrow \frac{w_1}{M_1}=\frac{w_2}{M_2}\end{aligned}$

w₁ = 15 , w₂ = 75

The molar mass of ethane M₁ = 30,

$\begin{aligned} & \Rightarrow \frac{15}{30}=\frac{75}{M_B} \\ & M_B=150\end{aligned}$
$(V \cdot D)_B=\frac{150}{2}=75$

Example 5: A cylinder with a movable piston contains 2 g of helium, He, at room temperature. More helium was added to the cylinder and the volume was adjusted so that the gas pressure remained the same. How many grams of helium were added to the cylinder if the volume (in g) was changed from 2 L to 2.7 L?

1)27

2)4.3

3)3.7

4) 0.7

Solution

We have,
Amount of He = 2g
Thus, moles of He = 2/4 = 0.5 moles
Initial volume(V_i) = 2 L
Final volume(V_f) = 2.7 L
Now, according to Avogadro’s law, we have

$\frac{V_i}{n_i}=\frac{V_f}{n_f}$

$\frac{2}{0.5}=\frac{2.7}{n_f}$

Total moles of He present in the cylinder

n_f = 0.675 moles

Thus the total amount of He = moles X molar mass.

So, the total amount of He = $0.675 \times 4=2.7 g$

Added amount = total amount - initial amount

Added amount = 2.7 - 2 = 0.7 g

Hence, 0.7 g of He is further added.

Summary

Gay-Lussac's Law describes the direct relationship of pressure with temperature for a gas at constant volume. In other words, the pressure and temperature are directly related to a constant volume. The law is formulated by Joseph Louis Gay-Lussac. It states that at constant volume, the pressure of a gas will increase if there is an increase in the temperature and decrease if there is a decrease in the temperature. .