Bcc Fcc Primitive Cubic Unit Cell - Definition, Structure, Types, FAQs
Have you ever wondered how atoms are actually arranged inside a solid? Why do some metals like iron have one type of packing while others like copper or sodium have a different one? You will all these answers by reading this article on FCC, BCC and primitive unit cell. The arrangement of atoms inside the material influences its properties. Like gold is very soft, malleable, and ductile, iron is tough and strong, while aluminium is light in weight. The difference in the properties is only because of the arrangement of atoms inside their unit cells.
- Unit Cell
- FCC structure
- BCC structure
- 1. Primitive Cubic Unit Cell
- 2. Body-centered Unit Cell (BCC)
- 3. Face-centered unit Cell (FCC)
- What is Lattice?
- Some Solved Examples

The unit cell is the smallest repetitive unit of the crystal lattice or a crystal structure. The 3D arrangement of atoms, molecules, or ions inside the given crystal is called a crystal lattice. There are three main types of unit cells: Simple cubic cell, Body-centered cubic unit cell, and Face-centred cubic unit cell. The unit structure of iron is BCC, which is why it’s strong, while the unit structure of Gold and aluminium is FCC, making them soft and malleable.
Unit Cell
The smallest group of atoms has the same number of crystals, and where the entire lattice can be formed by three dimensions is called the Cell Unit. Crystalline Solids exhibit a normal and repetitive pattern of existing particles.
Representation of the three-dimensional design of the particles present in the crystal, in which each particle is presented as a point in space known as a crystal lattice.
FCC structure
FCC (face-centered cubic): Atoms are usually arranged at the corners and even at the center of the surface of each given cell. Atoms are considered to affect the diagonals of the face. 4 atoms in a single unit cell. Atoms are arranged in the corners of the cube, and another atom is in the center of the cube.
BCC structure
The BCC unit cell has a total number of two atoms, one in the center and one in the eight from the corners. In the FCC system, there are also eight atoms in the corners of a cell cell with one atom centered on each surface. The atom on the surface is shared with a nearby cell.
What is an FCC structure and a BCC structure?
The most direct difference between FCC crystals and BCC is in the atomic systems. The cubic structure in the center of the face has an atom in all 8 positions, and in the center of all 6 faces. The body-centered cubic structure has atoms in all eight corner positions, and one is in the center of the cube.
Primitive meaning
1. Relating to, identifying, or preserving a first-degree character in the development of the appearance or history of a particular object.
2. Very basic or non-technical in terms of comfort, ease of use, or efficiency.
"Camp accommodation was old."
Types of Unit Cell
Multiple unit cells together form a crystal lattice. Physical particles such as atoms, and molecules also exist. Each lattice point remains such particles.
1. First Cubic Cell
2. Body-centered Body Unit Cell
3.A cell unit in the center of the face
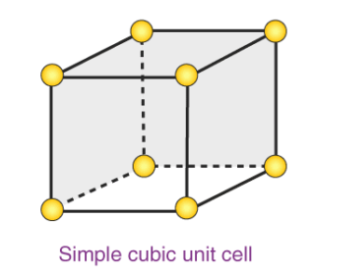
1. Primitive Cubic Unit Cell
In the first cell of the cubic unit, atoms are found only in the corners. Every atom in a corner is shared between cells in eight adjacent units. There are four unit cells in the same layer as 4 in the upper (or lower) layer. Thus, a single unit of cell has only 1 / 8th of an atom. Each subdivision in each of the following figures represents the particle center in that particular position and not its size. This building is known as the open-air building.
Atoms in the first phase of the simple cubic unit cell are found only in the corners
All the atoms in the corner are divided between the cells of the eight adjacent units
Four unit cells exist in the same layer
One unit cell is in the upper / lower layer
Thus, a single cell unit has only 18 atoms
Each subdivision in each of the following figures represents the particle center in that particular position and not its size
In each cell of the cubic unit, there are 8 atoms in the corners. Therefore, the total number of atoms in a single cell is
8 × 1/8 = 1 atom.
|
Related Topics |
2. Body-centered Unit Cell (BCC)
The BCC unit cell has atoms in each corner of the cube and the atom in the center of the structure. According to this structure, the atom in the center of the body entirely belongs to the cell unit in which it is located. In the BCC unit cell, every corner has atoms. There is one atom in the center of the building. At the bottom of the drawing is an open structure.
According to this, the atom of the structure in the physical organs is entirely the cell of the unit in which it is located.
Number of atoms in a BCC cell:
Therefore, in the BCC cell, we have:
8 x 1/8 corners with each atom = 8 × 1/8 = 1 atom
1 physical center atom = 1 × 1 = 1 atom
Hence, here the total number of atoms that are present per cell unit = 2 atoms.
Also read :
3. Face-centered unit Cell (FCC)
The FCC unit cell contains atoms in all corners of the crystal lattice and in the center of each cube surface. An atomic surface atom is divided between cells in two adjacent units, and only 1/2 of each atom is in each cell.
In the FCC unit cell, atoms are present in all corners of the crystal lattice
Also, there is an atom at the center of the whole surface of the cake
This atomic center is divided between cells in two adjacent units
Only about 12 atoms are part of a cell
Number of atoms in an FCC cell
a) 8 x 1/8 corners with each atom = 8 × 1/8 = 1 atom
b) Six surface atoms × 1/2 atom per unit of cell = 3 atoms
Therefore, the total number of atoms in a cell = 4 atoms
Therefore, in the cellic unit centered on the surface, we have:
8 x 1/8 corners with each atom = 8 × 1/8 = 1 atom
Six atoms centered on the surface × 1/2 atom per unit of cell = 3 atoms
Therefore, the total number of atoms in a cell = 4.
What is Lattice?
A lattice is a three-dimensional structure, a series of periodic points, on which a crystal is formed. In 1850, M. A. Bravais showed that similar points can be arranged geographically to produce 14 types of standard patterns. These 14 space fragments are known as Bravais lattices.
The crystal lattice of solidity can be defined according to its unit cell. A crystal lattice is made up of a very large number of unit cells, where every lattice point resides in a single particle. A unit cell can be seen as a three-dimensional structure consisting of one or more atoms.
We can see the volume of this cell unit in terms of cell unit size. For example, if we have a single edge cell “a”, the unit cell volume can be given as “a3”. The unit size of a cell is given as a measure of the size and volume of the cell. The unit size of a cell is equal to the product of the number of atoms in the cell and the size of each atom in the unit cell.
Quantity of cell unit = number of atoms per cell unit × size of each atom = z × m
Where, z = number of atoms in a cell,
m = Mass for each atomic mass
Atomic mass can be given with the help of Avogadro number and molar mass as:
MNA
Where, M = molar mass
NA number = Avogadro
Cell unit volume, V = a3
=> Multiple cell unit = maximum cell unit unit cell
=> Cell unit quantity = mV = z × ma3 = z × Ma3 × NA
Therefore, with the knowledge of the number of atoms in the unit cell, the marginal length and the molar size can determine the cell density of the unit.
A general description of the cell unit size of the various cases is found below:
1. The first cell unit: In the cell of the first unit, the number of atoms in a unit is equal to one. Therefore, the size is given by:
Maximum cell unit = 1 × Ma3 × NA
2. Cells centered in a cubic unit: In a cell-centered cubic unit cell, the number of atoms in a cell is equal to two. Therefore, the size is given by:
Maximum cell unit = 2 × Ma3 × NA
3. Cube-centered cubic unit cell: In a cell-centered cubic unit cell, the number of atoms in a unit cell is equal to four. Therefore, the size of the cell unit is given as:
Maximum cell unit = 4 × Ma3 × NA
Also check-
Some Solved Examples
Question 1: Which of the following statements is true regarding primitive unit cells?
1) They contain one or more constituent particles at positions other than corners.
2) (correct) They contain constituent particles only at the corner positions.
3) They contain one constituent particle at the body-centre besides the ones at the corners.
4) They contain one constituent particle present at the centre of each face besides the ones at the corners.
Solution:
Primitive and Centred Unit Cells
Primitive Unit Cells
When constituent particles are present only on the corner positions of a unit cell, it is called a primitive unit cell.
Centred Unit Cells
When a unit cell contains one or more constituent particles present at positions other than corners in addition to those at corners, it is called a centred unit cell. Centred unit cells are of three types:
- Body-Centred Unit Cells: Such a unit cell contains one constituent particle (atom, molecule or ion) at its body-centre besides the ones that are at its corners.
- Face-Centred Unit Cells: Such a unit cell contains one constituent particle present at the centre of each face, besides the ones that are at its corners.
- End-Centred Unit Cells: In such a unit cell, one constituent particle is present at the centre of any two opposite faces besides the ones present at its corners.
Primitive unit cells are defined as unit cells that contain only constituent particles at the corner positions. This means that there are no particles at any other positions within the unit cell. Therefore, option b) is the correct statement. Option a) describes centred unit cells, while options c) and d) describe specific types of centred unit cells (body-centred and face-centred, respectively).
Hence, the answer is option (2).
Question 2:
A metal crystallises with a FCC lattice. THe edge length pf unit cell is 408 pm. The diameter of metal atom is
1) (correct) 288 pm
2) 408 pm
3) 144 pm
4) 204 pm
Solution:
For the FCC lattice,
$
\begin{aligned}
& 4 r=a \sqrt{2} \\
& r=\frac{a \sqrt{2}}{4}=\frac{408}{2 \sqrt{2}}=144 \mathrm{pm} \\
& \text { diameter }=2 r=144 \times 2=288 \mathrm{pm}
\end{aligned}
$
Hence, the answer is option (1).
Question 3: In a simple cubic cell, each point on a corner is shared by
1) 2 unit cells
2) 1 unit cell
3) (correct) 8 unit cells
4) 4 unit cells
Solution:
Crystal Lattices and Unit Cells
A portion of the three-dimensional crystal lattice and its unit cell.
In the three-dimensional crystal structure, a unit cell is characterised by:
(i) its dimensions along the three edges a, b, and c. These edges may or may not be mutually perpendicular.
(ii) angles between the edges, α (between b and c), β (between a and c), and γ (between a and b). Thus, a unit cell is characterised by six parameters a, b, c, α, β, and γ.
Primitive Unit Cells
When constituent particles are present only on the corner positions of a unit cell, it is called a primitive unit cell.
Solution
As we learnt in
Primitive unit cell -
In a primitive unit cell, constituent particles are present only in the corner positions of the unit cell.
In the simple cubic cell, each point on a corner is shared by 8 unit cells.
Hence, the answer is option (3).
Practice More Questions With The Link Given Below
| Crystal Lattices and Unit Cells practice question and MCQs |
| Close Packed Structures practice question and MCQs |
Frequently Asked Questions (FAQs)
A primitive unit cell is the smallest repeating unit of a crystal lattice that can be used to construct the entire lattice through translation. It contains one or more atoms and reflects the symmetry and structure of the crystal.
BCC and FCC are two types of crystal structures found in metals and other materials. BCC has atoms positioned at the corners of a cube with one atom at the center, while FCC has atoms at each corner and the centers of each face of the cube.
A BCC unit cell effectively contains 2 atoms. There are 8 atoms located at the corners (contributing 1/8 each) and 1 atom in the center, totaling 2 atoms when added together.
An FCC unit cell contains 4 atoms. It has 8 corners (contributing 1/8 each) and 6 face-centered atoms (contributing 1/2 each), which totals to 4 atoms.
The packing efficiency of BCC is about 68%, while FCC boasts a higher packing efficiency of around 74%. Packing efficiency calculates the volume occupied by the atoms relative to the total volume of the unit cell.
The coordination number in a primitive cubic unit cell is 6. Each atom is surrounded by six nearest neighbors, one along each of the three axes in both positive and negative directions.
One primitive cubic unit cell effectively contains 1 atom. Although there are 8 atoms at the corners, each is shared by 8 adjacent unit cells, so 1/8 of each atom belongs to a single unit cell (8 × 1/8 = 1).
The packing efficiency of a primitive cubic structure is about 52.4%. This means that only 52.4% of the total volume is occupied by atoms, making it the least efficiently packed of the three cubic structures.
In a primitive cubic unit cell, the edge length (a) is equal to twice the atomic radius (r). This can be expressed as a = 2r, as the atoms at opposite corners of the cube just touch each other along the edge.
A primitive unit cell is the smallest possible unit cell that can be used to construct the entire lattice through translation. A conventional unit cell, while not always the smallest, is chosen for its symmetry and ease of visualization. For example, the conventional unit cell for a face-centered cubic structure is larger than its primitive unit cell but better illustrates the crystal's symmetry.
A BCC unit cell effectively contains 2 atoms. It has 8 corner atoms (each shared by 8 unit cells, contributing 1 atom) and 1 center atom (fully contained within the cell).
Primitive cubic structures are rare because they have the lowest packing efficiency (52.4%) among cubic structures. This inefficient use of space makes them less stable and energetically unfavorable compared to more efficiently packed structures like BCC or FCC.
Increasing pressure generally causes a decrease in unit cell parameters as atoms are forced closer together. This compression can lead to phase transitions, where the crystal adopts a more compact structure with a different unit cell. The degree of compression can vary in different directions for non-cubic crystals, leading to anisotropic behavior.
Symmetry operations (such as rotations, reflections, and inversions) that leave the crystal structure unchanged are crucial in categorizing and understanding crystal structures. They define the crystal system and space group of the material, which in turn determine many of its physical properties.
The unit cell structure greatly influences mechanical properties. For example, the slip systems (planes along which deformation occurs) are determined by the unit cell geometry. FCC structures typically have more slip systems than HCP, making FCC metals generally more ductile. The strength of interatomic bonds within the unit cell also affects properties like hardness and elastic modulus.
The coordination number increases from primitive cubic (6) to BCC (8) to FCC (12). This reflects the increasing number of nearest neighbors in each structure.
The FCC structure is more common in metals because it has a higher packing efficiency (74%) compared to primitive cubic (52.4%). This allows for more atoms to be packed into a given volume, resulting in a more stable and energetically favorable arrangement.
FCC has the highest packing efficiency at 74%, followed by BCC at 68%, and primitive cubic at 52.4%. This means FCC structures can accommodate more atoms in a given volume, making them more common in nature.
There are 4 octahedral voids in one FCC unit cell. These are located at the center of the unit cell and at the center of each edge.
A primitive cubic unit cell has atoms only at the corners of the cube. BCC has an additional atom at the center of the cube, while FCC has atoms at the center of each face in addition to the corner atoms.
Polymorphism occurs when a substance can exist in multiple crystal structures. Each polymorph has a different arrangement of atoms or molecules, resulting in different unit cell structures. This can lead to variations in properties such as solubility, melting point, and stability, despite having the same chemical composition.
Unit cells provide a framework for understanding how different atoms can be incorporated into a crystal structure. In substitutional alloys, atoms of one element replace some atoms of another in the unit cell. In interstitial solid solutions, smaller atoms fit into the voids (interstitial sites) of the host structure's unit cell. This concept helps explain the properties and behavior of alloys and solid solutions.
The atomic packing factor (APF) represents the fraction of volume in a unit cell that is occupied by atoms. It's a measure of how efficiently space is used in the crystal structure. A higher APF generally indicates a more stable structure and influences properties like density and melting point.
Vacancies or defects disrupt the perfect periodicity of the crystal structure. They can cause local distortions in the lattice, affecting properties like electrical conductivity, mechanical strength, and diffusion rates. While unit cells describe the ideal structure, real crystals often contain these imperfections.
The density of a crystal is directly related to its unit cell volume and the mass of atoms within it. It can be calculated by dividing the total mass of atoms in the unit cell by the unit cell volume. This relationship allows for the determination of crystal density from X-ray diffraction data.
A unit cell is the smallest repeating structural unit of a crystal lattice. It represents the basic arrangement of atoms, ions, or molecules that, when repeated in three dimensions, forms the entire crystal structure.
Lattice parameters are the dimensions and angles that define the unit cell of a crystal structure. For cubic structures, this is typically just the length of one side of the cube (a). For other structures, it may include multiple lengths (a, b, c) and angles (α, β, γ).
Unit cells are fundamental to X-ray diffraction analysis. The repeating pattern of unit cells in a crystal creates a regular array of scattering centers for X-rays. The diffraction pattern produced depends on the arrangement and spacing of atoms within the unit cell, allowing researchers to determine the crystal structure.
Unit cells provide insight into a material's properties by revealing its atomic arrangement. This arrangement influences characteristics such as density, melting point, conductivity, and mechanical properties. Understanding the unit cell structure helps predict and explain these macroscopic properties.
While cubic systems have equal edge lengths and 90° angles, non-cubic systems can have different edge lengths and/or angles. The unit cell concept still applies, but these cells may be described by more parameters. For example, a hexagonal close-packed (HCP) structure uses a hexagonal prism as its unit cell.
A close-packed structure refers to an arrangement of atoms or particles that maximizes the packing efficiency. In such structures, atoms are arranged to occupy the maximum possible space. FCC is an example of a close-packed structure.
An interstitial site is a void or empty space between atoms in a crystal structure. These sites can sometimes accommodate smaller atoms or ions, leading to interstitial solid solutions. The size and number of interstitial sites depend on the type of unit cell.
Generally, a higher coordination number leads to greater stability in crystal structures. This is because more nearest neighbors allow for stronger overall bonding and better distribution of forces within the crystal.
Generally, as temperature increases, the size of the unit cell increases due to thermal expansion. This is because higher temperatures cause atoms to vibrate more, increasing their average separation and thus the overall dimensions of the unit cell.
The number of atoms per unit cell increases from primitive cubic (1 atom) to BCC (2 atoms) to FCC (4 atoms). This reflects the increasing complexity and packing efficiency of these structures.
A lattice point is a mathematical point in space that defines the repeating pattern of the crystal structure. An atom is the physical particle occupying a position in the crystal. In some cases, atoms may be located at lattice points, but not all lattice points are necessarily occupied by atoms.
A Bravais lattice is an infinite array of discrete points with an arrangement and orientation that appears the same from any point of the array. There are 14 unique Bravais lattices in three dimensions, each describing a distinct crystal structure. Unit cells are the building blocks that, when repeated, form these lattices.
In molecular crystals, the unit cell contains whole molecules rather than individual atoms. The arrangement of these molecules within the unit cell determines properties like crystal shape, melting point, and solubility. Intermolecular forces (like hydrogen bonding or van der Waals forces) play a crucial role in stabilizing these structures.
The unit cell structure determines the arrangement of atoms and their electron orbitals, which directly influences the electronic band structure of the material. This affects properties like electrical conductivity, optical behavior, and magnetism. For instance, the difference between conductors, semiconductors, and insulators can often be explained by their unit cell structures and resulting electron configurations.
The unit cell structure affects how heat is transmitted through a crystal. In metals, where thermal conductivity is primarily due to free electrons, the structure influences electron mobility. In non-metals, where heat is conducted through lattice vibrations (phonons), the regularity and strength of bonds in the unit cell structure determine how efficiently these vibrations can propagate.
The c/a ratio in HCP structures is the ratio of the height of the unit cell (c) to the length of its hexagonal base (a). For an ideal HCP structure, this ratio is 1.633. Deviations from this ideal value can affect properties like ductility and slip systems in metals with HCP structures.
In an FCC structure, octahedral voids are larger than tetrahedral voids. The radius of an octahedral void is 0.414 times the radius of the sphere (atom), while the radius of a tetrahedral void is 0.225 times the radius of the sphere.
Phase transitions often involve changes in the unit cell structure. For example, a material might transition from one crystal structure to another as temperature or pressure changes. Understanding these transitions in terms of unit cell transformations helps explain changes in material properties and behavior during phase changes.
Wyckoff positions describe the symmetry-equivalent positions that atoms can occupy within a unit cell. They are crucial for fully specifying crystal structures, especially in more complex systems. Knowing the Wyckoff positions helps in understanding the symmetry of the crystal and in calculating properties like X-ray diffraction patterns.
Anisotropy, the variation of physical properties with direction, is often a direct result of the unit cell structure. Non-cubic crystals, in particular, tend to exhibit anisotropic behavior because their unit cells are not symmetrical in all directions. This can lead to direction-dependent properties like thermal expansion, electrical conductivity, and mechanical strength.
Twinning occurs when two or more crystals share some of the same crystal lattice points in a symmetrical manner. The unit cell structure determines the possible twinning modes by defining the symmetry elements and potential twinning planes. Understanding the unit cell helps predict and explain the occurrence and nature of twinning in different materials.
Quasicrystals challenge the traditional concept of unit cells as they lack periodicity while maintaining long-range order. Instead of a repeating unit cell, quasicrystals are described using higher-dimensional models projected onto three-dimensional space. This concept expands our understanding of possible atomic arrangements beyond conventional crystalline structures.
The reciprocal lattice is a mathematical construct that is inversely related to the real-space lattice of unit cells. It is crucial in understanding X-ray diffraction patterns and in describing the propagation of waves in crystals. Each point in the reciprocal lattice corresponds to a set of planes in the real-space lattice, facilitating the analysis of crystal structures.
The unit cell structure determines how light interacts with the crystal. It affects properties like refractive index, birefringence, and optical activity. In anisotropic crystals, the variation in atomic spacing in different directions within the unit cell leads to direction-dependent optical properties.
Piezoelectricity, the generation of electric charge in response to applied mechanical stress, is directly related to the symmetry of the unit cell. It occurs in crystals that lack a center of symmetry in their unit cell structure. Understanding the unit cell helps in predicting which materials will exhibit piezoelectric properties and in designing new piezoelectric materials.
The unit cell structure influences crystal growth by determining the energetically favorable directions and planes for atom or molecule addition. This affects the overall shape (habit) of macroscopic crystals. Understanding the unit cell can help predict growth rates in different crystallographic directions and explain phenomena like dendritic growth or faceting.
Bernal holes are interstitial voids found in certain close-packed structures, particularly in liquids and amorphous solids. While not directly related to the periodic unit cells of crystals, understanding these holes helps bridge the gap between crystalline and non-crystalline structures, providing insights into the atomic arrangements in materials that lack long-range order.
The unit cell structure determines the arrangement of magnetic moments in a material. In ferromagnetic materials, for example, the alignment of spins within and between unit cells leads to net magnetization. The symmetry of the unit cell also influences magnetic anisotropy, which is important in applications like data storage.
The unit cell structure plays a crucial role in superconductivity, particularly in high-temperature superconductors. Features like layered structures, specific atomic arrangements, and the presence of certain elements in defined positions within the unit cell can promote
Also Read
23 Aug'25 11:50 PM
10 Aug'25 11:42 AM
02 Jul'25 04:51 PM
02 Jul'25 04:50 PM
02 Jul'25 04:43 PM