Gay Lussac’s Law

This law states that the pressure of a given amount of gas is directly proportional to the absolute temperature provided the volume remains unchanged, feasibly named after the French chemist Joseph Louis Gay-Lussac, who formulated it in the early 19th century. It simply means that when the temperature of a gas increases, its pressure also increases, while in the case of a decrease in temperature, the pressure is decreased.

This Story also Contains

1. Gay-Lussac’s Law (Pressure-Temperature Relationship)
2. Some Solved Examples
3. Summary

Gay-Lussac’s Law (Pressure-Temperature Relationship)

Scientist Joseph Gay-Lussac as a result of his experiments gave a general relation between the temperature and the pressure of a gas. He found that the pressure of a given mass of a gas at constant volume is directly proportional to the temperature.
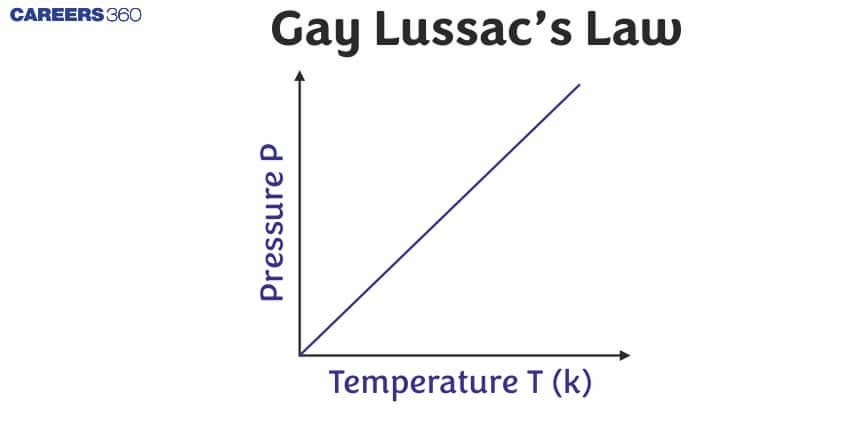
So, Gay-Lussac's Law or Pressure-Temperature Law can be stated as, At constant volume, the pressure of a fixed amount of a gas is directly proportional to the temperature.

The Law may be expressed mathematically as

$\mathrm{P} \propto \mathrm{T}$ ( volume, n are constant or $\mathrm{P}=k \mathrm{~T}$ $\frac{P}{T}=k,($ constant $)$

The above relationship can also be obtained by combining Boyle's Law and Charles's Law. For different conditions of pressure and temperature.

$
\begin{aligned}
& \frac{P_1}{T_1}=k=\frac{P_2}{T_2} \\
& \frac{P_1}{T_1}=\frac{P_2}{T_2}
\end{aligned}
$

When we know $P_1, T_1$ and $T_2$, then we can easily calculate the value of $P_2$

Plot between P vs T

Physical Significance of Gay Lussac's Law

It is seen that the pressure of the inflated tyres of automobiles is constant but in summers on a hot sunny day when the temperature IS high, then the pressure inside the tyres increases, and they may burst. Similarly in winters, on a cold morning, when the temperature is low, then the pressure inside the tyres decreases considerably.

Recommended topic video on (Gay Lussac’s Law)

Some Solved Examples

Example 1:
A rigid closed container contains an ideal gas at$ 27^{circ}$C temperature and 2 atm pressure. If the temperature is raised to $127^{circ}$C, what will be the final pressure of the gas in atm?

1)2.24

2)1.46

3)2.66

4)1.86

Solution:
Using Gay-Lussac’s Law:

$\frac{P_1}{T_1} = \frac{P_2}{T_2}$

Where:
$P_1 = 2 , {atm}$, $T_1 = 27 + 273 = 300K$, $T_2 = 127 + 273 = 400K$
Calculating $P_2$:

$\frac{2}{P_2} = \frac{300}{400} \implies P_2 = \frac{2 \times 400}{300} = 2.66 , {atm}$

Thus, the final pressure is 2.66 atm.

Example 2:
A tank contains a gas at a pressure of 3 atm at 303 K. If the tank can withstand a maximum pressure of 14 atm, will it melt or burst if the melting point of the tank is 2250 K?

1)Melt

2)Burst(correct)

3)Both occur simultaneously

4)Nothing can be predicted

Solution:
Using Gay-Lussac’s Law:
$\frac{P_1}{T_1} = \frac{P_2}{T_2}$
Where:
$P_1 = 3{atm}$, $T_1 = 303K$, $T_2 = 2250K$
Calculating $P_2$:
$P_2 = \frac{3 \times 2250}{303} \approx 22.3{atm}$
Since 22.3 atm exceeds 14 atm, the tank will burst.

Example 3:
A rigid nitrogen tank has a pressure of 30 atm at 06:00 am when the temperature is $27^{0}$C. At 03:00 pm, when the temperature is $45^{0}$C, what will be the pressure in the tank?

1)32

2)30

3)20

4)39

Solution:
Using Gay-Lussac’s Law:

$\frac{P_1}{T_1} = \frac{P_2}{T_2}$

Where:
$P_1 = 30{atm}$, $T_1 = 27 + 273 = 300K$, $T_2 = 45 + 273 = 318K$
Calculating P_2:

$\frac{30}{300} = \frac{P_2}{318} \implies P_2 = \frac{30 \times 318}{300} \approx 31.8 ,{atm} \approx 32 ,{atm}$

Thus, the pressure in the tank will be approximately 32 atm.

Example 4:
A gas is filled in a 10 L container with a pressure of 2 atm at $0^{0}$C. At what temperature (in °C) will the pressure inside the container be 2.5 atm?

1)68.25(correct)

2)73.78

3)65.45

4)56.89

Solution:
Using Gay-Lussac’s Law:
$\frac{P_1}{T_1} = \frac{P_2}{T_2}$
Where:
$P_1 = 2 , {atm}$, $P_2 = 2.5 ,{atm}$, $T_1 = 273K$
Calculating $T_2: $
$T_2 = \frac{2.5 \times 273}{2} = 341.25K \implies T_2 = 341.25 - 273 = 68.25^{0}C$
Thus, the temperature will be 68.25 °C.

Example 5:
A steel tank contains air at a pressure of 15 bar at $20^{0}$C. The tank has a safety valve that can withstand a pressure of 30 bar. Calculate the maximum temperature (in K) to which the tank can be heated safely.

1)578

2)600

3)498

4)586(correct)

Solution:
Using Gay-Lussac’s Law:

$\frac{P_1}{T_1} = \frac{P_2}{T_2}$

Where:
$P_1 = 15{bar}$, $P_2 = 30{bar}$, $T_1 = 20 + 273 = 293K$
Calculating $T_2$:

$T_2 = \frac{30 \times 293}{15} = 586K$

Thus, the maximum safe temperature is 586 K.

Summary

Gay-Lussac's law is very important in explaining how gases will behave in a closed system with constant volume. It describes the variation of pressure with temperature change, hence quite useful in many applications involving pressurized vessels and systems, like cookers, gas storage cylinders, and aerosol cans. Gay-Lussac's Law is important in its integration with other gas laws, all of which combined form the ideal gas law. It describes how temperature influences the pressure of gases; thus, it characterizes the behavior of gases at different temperatures.