Domain and Range of Inverse Trigonometric Functions

We know that trigonometric functions are periodic and hence, man-one in their actual domain. So, to define an inverse trigonometric function, we have to restrict its actual domain to make the function injective. In real life, we use the inverse trigonometric function for determining the depth of the hole or the angle of inclination.

This Story also Contains

1. Domain of Inverse Trigonometric Function
2. Rule to Find Domain of Inverse Trigonometric Functions
3. Range of Inverse Trigonometric Function
4. Domain and Range of $\sin ^{-1}(x)$
5. Domain and Range of $y=\cos ^{-1}(x)$
6. Domain and Range of $y=\tan ^{-1}(x)$
7. Domain and Range of $y=\cot ^{-1}(x)$
8. Domain and Range of $y=\sec ^{-1}(x)$
9. Domain and Range of $y=\operatorname{cosec}^{-1}(x)$

In this article, we will cover the concept of Domain and range of inverse Trigonometric Functions. This category falls under the broader category of Trigonometry, which is a crucial Chapter in class 12 Mathematics. It is not only essential for board exams but also for competitive exams like the Joint Entrance Examination(JEE Main) and other entrance exams such as SRMJEE, BITSAT, WBJEE, BCECE, and more. A total of eighteen questions have been asked on this topic including one in 2015, eight in 2021, and four in 2022, three in 2023.

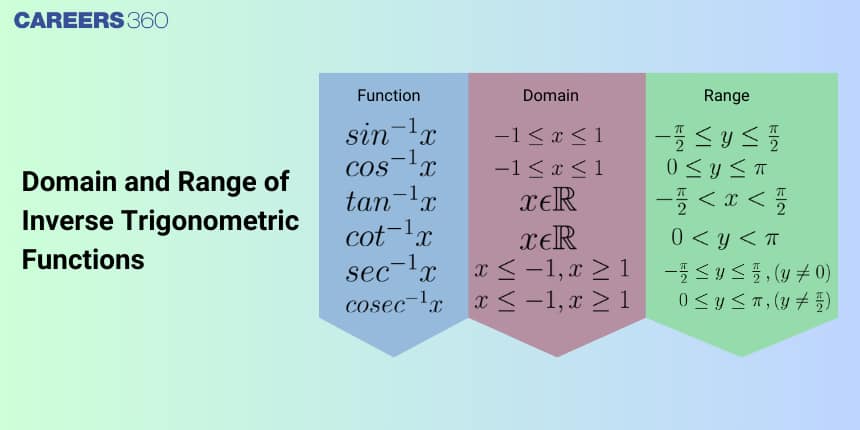
Domain of Inverse Trigonometric Function

Domain is defined as a set of numbers x for which$f(x)$ is true. The domain of an inverse function is equal to the range of the function.

Domain of $\sin ^{-1}(x)$ is $[-1,1]$ or $-1 \leq x \leq 1$
Domain of $\cos ^{-1}(x)=[-1,1]$
Domain of $\csc ^{-1}(x)=(-\infty,-1]$ or $[1,+\infty)$
Domain of $\sec ^{-1}(x)=(-\infty,-1]$ or $[1,+\infty)$
Domain of $\tan ^{-1}(\mathrm{x})=$ All Real Numbers
Domain of $\cot ^{-1}(x)=$ All Real Numbers

Rule to Find Domain of Inverse Trigonometric Functions

For any trigonometric function, we can find the domain using the below rule.

That is,

Domain (y^-1) = Range (y)

By knowing the range of trigonometric functions, we can get the domain of inverse trigonometric functions.

Range of Inverse Trigonometric Function

The range is defined as the set of values that the functions assume.

Range of $y=\sin ^{-1}(x)$ is,$-\pi / 2 \leq y \leq \pi / 2$
Range of $y=\cos ^{-1}(x)$ is $0 \leq y \leq \pi$
Range of $y=\csc ^{-1}(x)$ is $,-\pi / 2 \leq y \leq \pi / 2, y \neq 0$
Range of $y=\sec ^{-1}(x)$ is $0 \leq y \leq \pi, \quad y \neq \pi / 2$
Range of $y=\sec ^{-1}(x)$ is $0 \leq y \leq \pi, \quad y \neq \pi / 2$
Range of $y=\sec ^{-1}(x)$ is $0 \leq y \leq \pi, \quad y \neq \pi / 2$

Domain and Range of $\sin ^{-1}(x)$

$y=\sin ^{-1}(x)$

The function $y=\sin (x)$ is Many one so it is not invertible. Now consider the small portion of the function

$y=\sin x, x \in\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$ and $y \in[-1,1]$

Which is strictly increasing, Hence, one-one and inverse is$y=\sin ^{-1}(x)$

Domain is $[-1,1]$ and Range is $\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]$

Domain and Range of $y=\cos ^{-1}(x)$

$y=\cos ^{-1}(x)$

Domain is $[-1,1]$ and Range is $[0, \pi]$

Domain and Range of $y=\tan ^{-1}(x)$

Domain is $\mathbb{R}$ and Range is $\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)$

Domain and Range of $y=\cot ^{-1}(x)$

Domain is $\mathbb{R}$ and Range is $(0, \pi$

Domain and Range of $y=\sec ^{-1}(x)$

Domain is $\mathbb{R}-(-1,1)$ and Range is $[0, \pi]-\left\{\frac{\pi}{2}\right\}$

Domain and Range of $y=\operatorname{cosec}^{-1}(x)$

Domain is $\mathbb{R}-(-1,1)$ and Range is $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]-\{0\}$

Recommended Video Based on Domain and Range of Inverse Trigonometric Functions:

Solved Examples Based on Domain and Range of Trigonometric Functions

Example 1: Let D be the domain of the function $f(x)=\operatorname{Sin}^{-1}\left(\log _{3 x}\left(\frac{6+2 \log _3 x}{-5 x}\right)\right)$. If the range of the function $g: D \rightarrow R$ defined by $g(x)=x-[x],([x]$ is the greatest integer function ), is $(\alpha, \beta)$, then $\alpha^2+\frac{5}{\beta}$ is equal to [JEE MAINS 2023]

Solution

$\begin{aligned} & \frac{6+2 \log _3 x}{-5 x}>0 \& x>0 \& x \neq \frac{1}{3} \\ & \text { this gives } x \in\left(0, \frac{1}{27}\right) \ldots(1) \\ & -1 \leq \log _{3 x}\left(\frac{6+2 \log _3 x}{-5 x}\right) \leq 1 \\ & 3 x \leq \frac{6+2 \log _3 x}{-5 x} \leq \frac{1}{3 x}\end{aligned}$$\begin{array}{ll}15 x^2+6+2 \log _3 x \geq 0 & 6+2 \log _3 x+\frac{5}{3} \geq 0 \\ x \in\left(0, \frac{1}{27}\right) \ldots(2) & x \geq 3^{-\frac{23}{6}} \ldots(3) \\ \text { form }(1),(2) \&(3) & \\ x \in\left[3^{-\frac{23}{6}}, \frac{1}{27}\right) & \end{array}$
$
\begin{aligned}
& \text { form(1),(2)\&(3) } \\
& x \in\left[3^{\frac{23}{6}}, \frac{1}{27}\right)
\end{aligned}
$

$\therefore \alpha$ is small positive quantity
$\& \beta=\frac{1}{27}$
$\therefore \alpha^2+\frac{5}{\beta}$ is just greater than 135

Hence, the answer is 135

Example 2: If the domain of the function $f(x)-\log _e\left(4 x^2+11 x+6\right)+\sin ^{-1}(4 x+3)+\cos ^{-1} \frac{10 x+6}{3}$ is $(\alpha, \beta)$, then $36|\alpha+\beta|$ is equal to [JEE MAINS 2023]

Solution
$
\begin{aligned}
& f(x)=\ln \left(4 x^2+11 x+6\right)+\sin ^{-1}(4 x+3) \\
& +\cos ^{-1}\left(\frac{10 x+6}{3}\right)
\end{aligned}
$
$
\begin{aligned}
& \text { (i) } 4 x^2+11 x+6>0 \\
& 4 x^2+8 x+3 x+6>0 \\
& (4 x+3)(x+2)>0 \\
& x \in(-\infty,-2) \cup\left(-\frac{3}{4}, \infty\right)
\end{aligned}
$
$
\begin{aligned}
& \text { (ii) } 4 x+3 \in[-1,1] \\
& x \in[-1,-1 / 2]
\end{aligned}
$
$
\begin{aligned}
& \text { (iii) } \frac{10 x+6}{3} \in[-1,1] \\
& x \in\left[-\frac{9}{10},-\frac{3}{10}\right] \\
& x \in\left(-\frac{3}{4},-\frac{1}{2}\right] \\
& \alpha+\beta=-\frac{5}{4} \\
& 36|\alpha+\beta|=45
\end{aligned}
$
Hence, the answer is 45

Example 3: If the domain of the function $f(x)=\frac{\cos ^{-1} \sqrt{x^2-x+1}}{\sqrt{\sin ^{-1}\left(\frac{2 x-1}{2}\right)}}$is the interval$(\alpha, \beta)$, then $\alpha+\beta$ is equal to: [JEE MAINS 2021]

Solution

$f(x)=\frac{\cos ^{-1} \sqrt{x^2-x+1}}{\sqrt{\sin ^{-1}\left(\frac{2 x-1}{2}\right)}}$

For domain $-1 \leqslant \sqrt{x^2-x+1} \leqslant 1$ and $x^2-x+1 \geqslant 0$

$\begin{aligned} & \Rightarrow \quad \sqrt{x^2-x+1} \leqslant 1 \text { and } x^2-x+1 \geqslant 0 \\ & \Rightarrow x^2-x+1 \leqslant 1 \text { and } x^2-x+1 \geqslant 0 \\ & \Rightarrow \quad x^2-x \leqslant 0 \text { and } x \in R(\text { as } D<0, a>0) \\ & \Rightarrow x(x-1) \leqslant 0 \text { and } x \in R\end{aligned}$

$\Rightarrow x \in[0,1]$

For,

$\frac{1}{\sqrt{\sin ^{-1}\left(\frac{2 x-1}{2}\right)}}$

$\sin ^{-1}\left(\frac{2 x-1}{2}\right)>0$ and $-1 \leqslant \frac{2 x-1}{2} \leqslant 1$

$\begin{aligned} & \Rightarrow 0<\frac{2 x-1}{20} \leqslant 1 \text { and }-1 \leqslant \frac{2 x-1}{2} \leqslant 1 \\ & \Rightarrow 0<\frac{2 x-1}{2} \leqslant 1 \\ & \Rightarrow \quad 0<x-\frac{1}{2} \leq 1 \\ & \Rightarrow \frac{1}{2}<x \leqslant \frac{3}{2} .\end{aligned}$

Domain for $f(x)$ will be the intersection of these results.

$\begin{aligned} & \Rightarrow \quad x \in\left(\frac{1}{2}, 1\right] \\ & \Rightarrow \alpha=\frac{1}{2}, \beta=1 \Rightarrow \alpha+\beta=\frac{3}{2}\end{aligned}$

Hence, the answer is $\frac{3}{2}$

Example 4: The domain of the function $f(x)=\sin ^{-1}\left(\frac{x^2-3 x+2}{x^2+2 x+7}\right)$ is: [JEE MAINS 2022]

Solution

For domain

$
-1 \leq \frac{x^2-3 x+2}{x^2+2 x+7} \leq 1
$
As the denominator is positive ( $D_j 0$ )

$
-\left(x^2+2 x+7\right) \leq x^2-3 x+2 \leq x^2+2 x+7
$
Solving first

$
\begin{aligned}
& -x^2-2 x-7 \leqslant x^2-3 x+2 \\
& \Rightarrow 2 x^2-x+9 \geqslant 0 \\
& \Rightarrow x \in R \quad(\text { as } D<0)
\end{aligned}
$
Solving second

$
\begin{aligned}
& \mathrm{x}^2-3 \mathrm{x}+2 \leqslant \mathrm{x}^2+2 \mathrm{x}+7 \\
\Rightarrow & 5 \mathrm{x}+5 \geqslant 0 \\
\Rightarrow & x \geqslant-1 \\
\therefore \quad & \mathrm{x} \geqslant-1
\end{aligned}
$

Hence, the answer is the $[-1, \infty)$

Example 5: Considering only the principal values of the inverse trigonometric functions, the domain of the function $f(x)=\cos ^{-1}\left(\frac{x^2-4 x+2}{x^2+3}\right)$ is:[JEE MAINS 2022]

Solution

$\begin{aligned} & \left|\frac{x^2+4 x+2}{x^2+3}\right| \leq 1 \\ & \left(x^2-4 x+2\right)^2 \leq\left(x^2+3\right)^2 \\ & \left(x^2-4 x+2\right)^2-\left(x^2+3\right)^2 \leq 0 \\ & \left(2 x^2-4 x+5\right)(-4 x-1) \leq 0 \\ & -4 x-1 \leq 0 \rightarrow x \geq-\frac{1}{4} \\ & {\left[-\frac{1}{4}, \infty\right)}\end{aligned}$

Hence, the answer is the $\left[-\frac{1}{4}, \infty\right)$