Excenter of a triangle

The excenter of a triangle is a special point where the internal bisector of one angle and the external bisectors of the other two angles meet. Every triangle has three excenters, each corresponding to one of its vertices, and each excenter serves as the centre of an excircle that touches one side of the triangle and the extensions of the other two. For example, the A-excenter is associated with vertex $A$ and its excircle touches sides $AB$, $AC$, and $BC$ at specific tangency points whose locations can be determined using the excenter of a triangle formula in mathematics. The study of excenters involves understanding their properties, deriving the coordinates of an excenter from the triangle’s vertices, finding the distance between the incenter and excenter, and exploring the geometry of the points of tangency. In this article, we will cover these definitions, formulas, coordinate derivations, and important properties in detail.

What is the Excenter of a Triangle?

The excenter of a triangle is a special point in geometry that acts as the centre of a circle, called the excircle, which touches one side of the triangle externally and the extensions of the other two sides. Every triangle has three excenters, each corresponding to one vertex.

In coordinate geometry, the excenter of a triangle formula is used to calculate the location of this point using the vertices and side lengths. The excenter is also linked to important properties of excenter and points of tangency that are widely used in both pure and applied mathematics.

Definition of Excenter in Geometry

In geometry, an excenter is defined as the intersection point of two external angle bisectors and one internal angle bisector of a triangle.

For a triangle $ABC$, the excenter opposite vertex $A$ is denoted as $I_A$ (also called the A-excenter). The A-excircle associated with $I_A$ touches:

• side $BC$ at tangency point $D$

• the extension of side $AB$ at $E$

• the extension of side $AC$ at $F$

If $a$, $b$, and $c$ are the lengths of sides $BC$, $CA$, and $AB$ respectively, and $(x_A, y_A)$, $(x_B, y_B)$, $(x_C, y_C)$ are their coordinates, the formula for coordinates of the excenter opposite $A$ is:

$I_A = \left( \frac{-a \cdot x_A + b \cdot x_B + c \cdot x_C}{-a + b + c}, \frac{-a \cdot y_A + b \cdot y_B + c \cdot y_C}{-a + b + c} \right)$

Understanding the Concept of Excentre and Excircle

The excentre always lies outside the triangle and serves as the center of the excircle.

The radius of the excircle opposite $A$ is:

$r_A = \frac{\Delta}{s-a}$

where:

• $\Delta$ is the area of the triangle

• $s = \frac{a+b+c}{2}$ is the semi-perimeter

• $a$ is the length of side $BC$

The points of tangency between the excircle and the sides can be calculated using the formula for the coordinates of the excenter and the points of tangency in a triangle, which is particularly useful in coordinate geometry.

Difference Between Incenter and Excenter

While the incenter is the intersection of the three internal angle bisectors and is the centre of the incircle (which touches all sides internally), the excenter involves two external and one internal angle bisector.

Key differences:

This distinction helps in applying the properties of excenter and points of tangency in a triangle to both theoretical and coordinate-based problems.

Excentre of Triangle Formula

An excenter is a point where the bisector of one interior angle of a triangle meets the bisectors of the two exterior angles at the other two vertices.

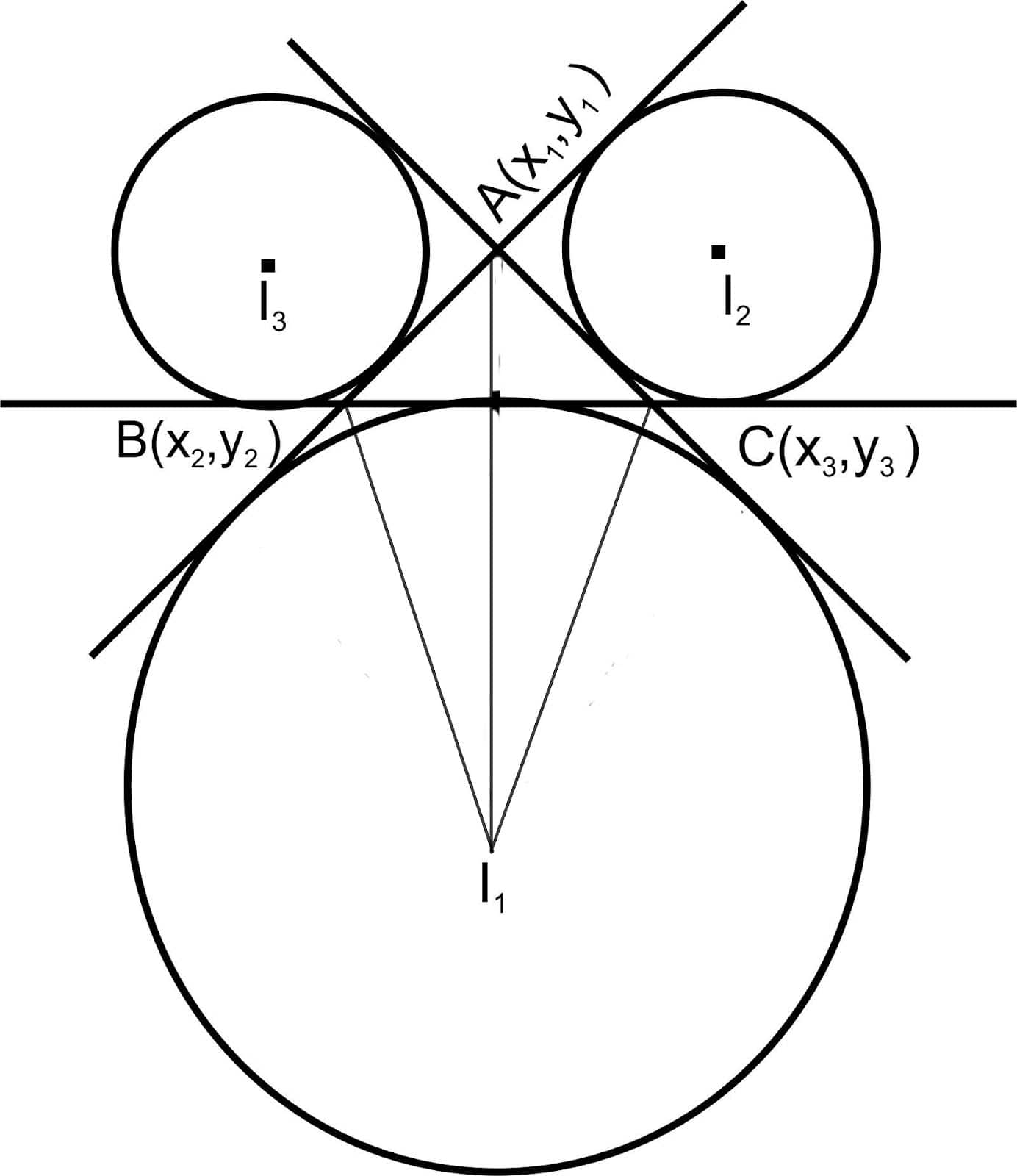
Let $A(x_1, y_1)$, $B(x_2, y_2)$, and $C(x_3, y_3)$ be the vertices of $\triangle ABC$, such that:

• $BC = a$

• $CA = b$

• $AB = c$

The circle that touches the side $BC$, and the extensions of $AB$ and $AC$, is called the escribed circle opposite the angle $A$.

The bisectors of the external angles at $B$ and $C$ meet at a point $I_1$, which is the center of the escribed circle opposite $A$. If $I_1$ is the intersection of the internal bisector of $\angle BAC$ and the external bisectors of $\angle ABC$ and $\angle ACB$, then the coordinates of the three excenters are:

A-excenter $I_1$:

$I_1 = \left( \frac{-a x_1 + b x_2 + c x_3}{-a + b + c}, \frac{-a y_1 + b y_2 + c y_3}{-a + b + c} \right)$

B-excenter $I_2$:

$I_2 = \left( \frac{a x_1 - b x_2 + c x_3}{a - b + c}, \frac{a y_1 - b y_2 + c y_3}{a - b + c} \right)$

C-excenter $I_3$:

$I_3 = \left( \frac{a x_1 + b x_2 - c x_3}{a + b - c}, \frac{a y_1 + b y_2 - c y_3}{a + b - c} \right)I$

Properties of the Excenter of a Triangle

The properties of the excenter (or excentre) of a triangle are fundamental in both pure geometry and coordinate geometry. These properties explain the location of each excenter, its relationship with the points of tangency, and various geometrical and algebraic characteristics. The formula for the coordinates of the excenter and points of tangency in a triangle allows precise calculation in analytical geometry.

Location of Each Excenter in a Triangle

A triangle $ABC$ has three excenters, each corresponding to one vertex:

• A-excenter $I_A$ : opposite vertex $A$

• B-excenter $I_B$ : opposite vertex $B$

• C-excenter $I_C$ : opposite vertex $C$

If $(x_A, y_A)$, $(x_B, y_B)$, and $(x_C, y_C)$ are the vertices, and $a$, $b$, and $c$ are the lengths of $BC$, $CA$, and $AB$ respectively, then:

$I_A = \left( \frac{-a \cdot x_A + b \cdot x_B + c \cdot x_C}{-a + b + c}, \frac{-a \cdot y_A + b \cdot y_B + c \cdot y_C}{-a + b + c} \right)$

Similarly, $I_B$ and $I_C$ are found by cyclic permutations of $a$, $b$, and $c$.

Relationship Between Excenter and Points of Tangency

The A-excircle touches:

• Side $BC$ at point $D$

• Extension of $CA$ at point $E$

• Extension of $AB$ at point $F

If $s$ is the semi-perimeter of $\triangle ABC$, then:

$BD = s - b \quad \text{and} \quad DC = s - c$

These tangency points can be computed using the formula for the coordinates of excenter and the points of tangency in a triangle, allowing accurate placement in coordinate geometry.

Key Geometrical Properties of Excenters

Properties of Excentre:

1. External position: Excenters always lie outside the triangle.

2. Equilateral triangle property: The excentres of an equilateral triangle are equidistant from each other, and this distance is twice the side of the triangle.

3. Tangent circle property: Each excenter is the centre of an excircle tangent to one side of the triangle and the extensions of the other two sides.

4. Angle bisector property: The excenter is the intersection point of the internal angle bisector of one vertex and the external angle bisectors of the other two vertices.

5. Collinearity with orthocenter: The three excenters and the orthocenter of the triangle are collinear.

6. Orthocentric system property: The incenter and the three excenters form an orthocentric system, with the incenter as the orthocenter of the triangle formed by the excenters.

Additional mathematical facts:

• Exradius formula: The radius of the excircle opposite $A$ is
  $r_A = \frac{\Delta}{s-a}$
  where $\Delta$ is the area of the triangle and $s$ is the semi-perimeter.

• Distance between incenter and excenter:
  $II_A = \sqrt{R(R - 2r)}$
  where $R$ is the circumradius and $r$ is the inradius.

Solved Examples Based on Excentre of a triangle

Example 1: If $\triangle ABC$ is an equilateral triangle of side $a$, then find the minimum distance between two excenters.

Solution: Let in $\triangle ABC$, $A(0,0)$, $B\left(\frac{a}{2}, \frac{\sqrt{3}a}{2}\right)$, and $C(a, 0)$.

Coordinates of $I_1$:
$ I_1 \equiv \left( \frac{-a x_1 + b x_2 + c x_3}{-a + b + c}, \frac{-a y_1 + b y_2 + c y_3}{-a + b + c} \right) $

Coordinates of $I_2$:
$ I_2 \equiv \left( \frac{a x_1 - b x_2 + c x_3}{a - b + c}, \frac{a y_1 - b y_2 + c y_3}{a - b + c} \right) $

Coordinates of $I_3$:
$ I_3 \equiv \left( \frac{a x_1 + b x_2 - c x_3}{a + b - c}, \frac{a y_1 + b y_2 - c y_3}{a + b - c} \right) $

For $I_1$:
$ I_1 = \left( \frac{-a \cdot 0 + a \cdot a + a \cdot \frac{a}{2}}{-a + a + a}, \frac{-a \cdot 0 + a \cdot 0 + a \cdot \frac{\sqrt{3}a}{2}}{-a + a + a} \right) $

$ I_1 = \left( \frac{\frac{3a^2}{2}}{a}, \frac{\frac{\sqrt{3}a^2}{2}}{a} \right) $

$ I_1 = \left( \frac{3a}{2}, \frac{\sqrt{3}a}{2} \right) $

Hence, the minimum distance between two excenters is: $ 2a $.

Example 2: $ABC$ is an equilateral triangle such that the vertices $B$ and $C$ lie on two parallel lines at a distance $6$. If $A$ lies between the parallel lines at a distance $4$ from one of them, then find the length of a side of the equilateral triangle.

Solution: From the choice of the axis:
$ A = (0,0) $

$ B = \left( 2 \cot \theta, \ 2 \right) $

$ C = \left( 4 \cot\left(60^\circ - \theta\right), \ -4 \right) $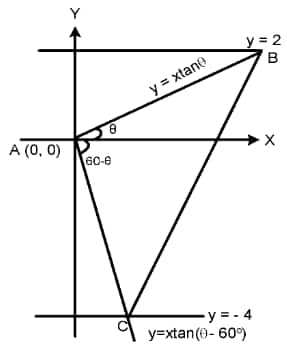

Now, $(\text{side of equilateral triangle})^2$

$= 4 \cot^2 \theta + 4 = 16 \cot^2(60^\circ - \theta) + 16$

$\Rightarrow 4 \csc^2 \theta = 16 \csc^2(60^\circ - \theta)$

$\Rightarrow \tan \theta = \frac{\sqrt{3}}{5}$

Hence, the required length is $2 \csc \theta = 4 \sqrt{\frac{7}{3}}$

Therefore, the correct answer is $4 \sqrt{\frac{7}{3}}$.

Example 3: $P(x, y)$ is called a good point if $x, y \in \mathbb{N}$. The total number of good points lying inside the quadrilateral formed by the lines $2x + y = 2$, $x = 0$, $y = 0$ and $x + y = 5$ is equal to:

Solution: The adjacent figure indicates that there are exactly $6$ good points inside the quadrilateral $ABCD$.

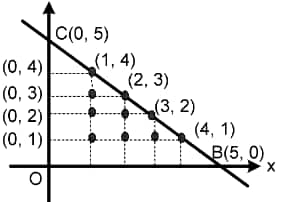
Hence, the correct answer is $6$.

Example 4: If the point $P(a, a^2)$ lies completely inside the triangle formed by the lines $x = 0$, $y = 0$ and $x + y = 2$, then the exclusive range of $a$ is:

Solution:
Clearly $a \in \mathbb{R}^+$.

Also $a^2 + a - 2 < 0$.

$\Rightarrow (a + 2)(a - 1) < 0$

$\Rightarrow -2 < a < 1$

$\Rightarrow a \in (0, 1)$

Hence, the correct answer is $a \in (0, 1)$.

Example 5: If one vertex of an equilateral triangle of side $2$ is the origin and another vertex lies on the line $x = \sqrt{3},y$, then the third vertex can be:

Solution:
Clearly, the third vertex will lie on the $y$-axis.

Hence, the points are $(0, 2)$ or $(0, -2)$.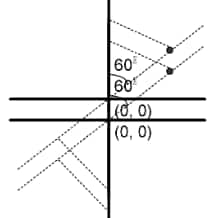

Hence, the correct answer is (0,2).