Circumcenter of a Triangle and Its Formula

Circumcentre: Definition

The circumcentre ($O$) of a triangle is the point of intersection of the perpendicular bisectors of the triangle’s sides. A perpendicular bisector of a side is a line that passes through the midpoint of the side and is perpendicular to it.

The circumcentre is also defined as the centre of the circle that passes through all three vertices of the triangle. This circle is called the circumcircle, and the circumcentre is its centre.

Key properties of the circumcentre based on triangle type:

• In an acute-angled triangle, the circumcentre lies inside the triangle.

• In an obtuse-angled triangle, the circumcentre lies outside the triangle.

• In a right-angled triangle, the circumcentre is located at the midpoint of the hypotenuse.

Thus, the circumcentre is the point where all perpendicular bisectors of a triangle are concurrent and serves as the centre of the circumcircle.

Circumcentre of a Triangle: Formula

Let $A$, $B$, and $C$ be the vertices of triangle $ABC$ with coordinates $A(x_1, y_1)$, $B(x_2, y_2)$, and $C(x_3, y_3)$.

Then, the coordinates of the circumcentre ($O$) are given by: $(x_c, y_c) = \left( \frac{x_1 \sin 2A + x_2 \sin 2B + x_3 \sin 2C}{\sin 2A + \sin 2B + \sin 2C}, \frac{y_1 \sin 2A + y_2 \sin 2B + y_3 \sin 2C}{\sin 2A + \sin 2B + \sin 2C} \right)$

Note: For a right-angled triangle, the circumcentre is the midpoint of the hypotenuse, and the coordinates simplify to:

$(x_c, y_c) = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$

Properties of Circumcircle and Circumcentre

1. The perpendicular from the center of a circle to any chord bisects the chord. Therefore, the circumcentre of a triangle is the point of concurrency of the perpendicular bisectors of its sides.

2. The distance of the circumcentre from all three vertices of the triangle is the same. This distance is called the circumradius ($R$):
   $OA = OB = OC = R$

3. The angle subtended by a chord at the center of the circumcircle is twice the angle subtended by the same chord at any point on the circumference:
   $\angle AOB = 2 \times \angle ACB$

4. The distance of the circumcentre from the sides of the triangle can be expressed using the circumradius. For example, if $O$ is the circumcentre and $E$ and $F$ are points on sides of the triangle:
   $OE = R \cos B, \quad OF = R \cos C$

5. In an acute-angled triangle, the circumcentre lies inside the triangle.

6. In an obtuse-angled triangle, the circumcentre lies outside the triangle.

7. In a right-angled triangle, the circumcentre is located at the midpoint of the hypotenuse.

Circumcenter in Special Triangles

The circumcenter’s location changes based on the type of triangle, which affects how we calculate it and its applications in geometry. Knowing its position helps in constructions, finding circumcircle radius, and solving coordinate geometry problems.

Circumcenter of an Equilateral Triangle

In an equilateral triangle, all sides are equal, and all angles are $60^\circ$. The circumcenter coincides with the centroid and incenter. It lies exactly at the center of the triangle, making construction and distance calculations straightforward.

Coordinates of the circumcenter in an equilateral triangle with vertices $A(x_1, y_1)$, $B(x_2, y_2)$, $C(x_3, y_3)$ are:

$(x_c, y_c) = \left( \frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3} \right)$

The circumradius $R$ is calculated as: $R = \frac{a}{\sqrt{3}}$

where $a$ is the length of a side.

This makes equilateral triangles simple to work with in geometry problems and competitive exam questions.

Circumcenter of a Right-Angled Triangle

For a right-angled triangle, the circumcenter always lies at the midpoint of the hypotenuse. This is because the hypotenuse acts as the diameter of the circumcircle.

If the hypotenuse has endpoints $A(x_1, y_1)$ and $B(x_2, y_2)$, the circumcenter coordinates are:

$(x_c, y_c) = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$

The circumradius is: $R = \frac{\text{Hypotenuse}}{2}$

This property simplifies calculations and is particularly useful for geometry problems involving right triangles and circle constructions.

Circumcenter of an Isosceles and Scalene Triangle

In an isosceles triangle, the circumcenter lies on the axis of symmetry. In scalene triangles, it can be inside or outside the triangle depending on the angles. For any triangle with vertices $A(x_1, y_1)$, $B(x_2, y_2)$, $C(x_3, y_3)$, the coordinates of the circumcenter are given by:

$x_c = \frac{(x_1^2 + y_1^2)(y_2 - y_3) + (x_2^2 + y_2^2)(y_3 - y_1) + (x_3^2 + y_3^2)(y_1 - y_2)}{2 \left( x_1(y_2 - y_3) - y_1(x_2 - x_3) + x_2 y_3 - x_3 y_2 \right)}$

$y_c = \frac{(x_1^2 + y_1^2)(x_3 - x_2) + (x_2^2 + y_2^2)(x_1 - x_3) + (x_3^2 + y_3^2)(x_2 - x_1)}{2 \left( x_1(y_2 - y_3) - y_1(x_2 - x_3) + x_2 y_3 - x_3 y_2 \right)}$

This formula works for both isosceles and scalene triangles and is essential in coordinate geometry and competitive exams for accurately finding the circumcenter.

How to Construct a Circumcenter Geometrically

Constructing the circumcenter accurately is important for geometric problems, triangle constructions, and creating circumcircles in real-life applications.

Using Compass and Straightedge

1. Draw the perpendicular bisector of at least two sides of the triangle using a compass and straightedge.

2. The intersection of these perpendicular bisectors is the circumcenter:

(xc,yc)(x_c, y_c)(xc,yc)

This method is fundamental in manual geometry constructions and helps visualize the circumcenter in any triangle.

Perpendicular Bisector Method

For a triangle with vertices $A(x_1, y_1)$, $B(x_2, y_2)$, $C(x_3, y_3)$:

Find the midpoints of sides:

$M_{AB} = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right), \quad M_{BC} = \left( \frac{x_2 + x_3}{2}, \frac{y_2 + y_3}{2} \right)$

Draw perpendicular lines at these midpoints.

Solve for their intersection to get the circumcenter coordinates: $(x_c, y_c)$

This method is widely used in coordinate geometry and ensures accurate circumcircle construction for any triangle type.

Solved Examples Based on Circumcentre

Example 1: Let $\mathrm{C}(\alpha, \beta)$ be the circumcenter of the triangle formed by the lines

$\begin{aligned} & 4 x+3 y=69 \\ & 4 y-3 x=17 \text { and } \\ & x+7 y=61\end{aligned}$

Then $(\alpha-\beta)^2+\alpha+\beta$ is equal to [JEE MAINS 2023]

Solution:

$25y = 175$
$y = 7, \quad x = 12$
$A(12, 7)$
$-3x + 4y = 17$
$3x + 21y = 183$
$25y = 200$
$y = 8, \quad x = 5$
$B(5, 8)$
$\therefore \text{Circumcenter}$
$\alpha = \frac{17}{2}, \quad \beta = \frac{15}{2}$
$\left(\frac{17}{2}, \frac{15}{2}\right)$
$(\alpha - \beta)^2 + \alpha + \beta$
$1 + 16 = 17$

Hence, the answer is $17$.

Example 2: If the points $P$ and $Q$ are respectively the circumcenter and the orthocentre of a $\triangle \mathrm{ABC}$, the $\overrightarrow{\mathrm{PA}}+\overrightarrow{\mathrm{PB}}+\overrightarrow{\mathrm{PC}}$ is equal to [JEE MAINS 2023]

Solution:

$\begin{aligned} & \overrightarrow{\mathrm{PA}}+\overrightarrow{\mathrm{PB}}+\overrightarrow{\mathrm{PC}}=\vec{a}+\vec{b}+\vec{c} \\ & \overrightarrow{\mathrm{PG}}=\frac{\overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}+\vec{c}}{3} \\ & \Rightarrow \overrightarrow{\mathrm{a}}+\overrightarrow{\mathrm{b}}+\overrightarrow{\mathrm{c}}=3 \overrightarrow{\mathrm{PG}}=\overrightarrow{\mathrm{PQ}}\end{aligned}$

Hence, the answer is $\overrightarrow{P Q}$.

Example 3: In $\triangle A B C$, let $A D$ be the median and $O, G, P$ be respectively the circumcentre, centroid and orthocentre. Then $\triangle O G D$ is directly similar to

Solution:

Trigonometric Ratios of Functions -

$\sin \Theta = \frac{\text{Opp}}{\text{Hyp}}$
$\cos \Theta = \frac{\text{Base}}{\text{Hyp}}$
$\tan \Theta = \frac{\text{Opp}}{\text{Base}}$

wherein

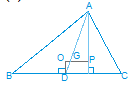
From figure, we can observe that $\triangle O G D$ is directly similar to $\triangle P G A$.

List of Topics Related to the Circumcenter of a triangle

Explore key topics connected to the circumcenter of a triangle, including formulas, properties, solved examples, and important concepts that help in mastering coordinate geometry and competitive exam preparation.

NCERT Resources

Access comprehensive NCERT resources for Chapter 10 – Straight Lines, including Class 11 Maths notes, solutions, and exemplar problems. These materials help students understand concepts, practice effectively, and excel in exams.

NCERT Class 11 Maths Notes for Chapter 10 - Straight Lines

NCERT Class 11 Maths Solutions for Chapter 10 - Straight Lines

NCERT Class 11 Maths Exemplar Solutions for Chapter 10 - Straight Lines

Practice Questions based on the Circumcenter of a triangle

Solve these carefully designed practice questions on the circumcenter of a triangle to strengthen your understanding of formulas, properties, and construction methods. These circumcenter problems will help you master geometry concepts and improve exam preparation.

Circumcircle Of A Triangle - Practice Question MCQ

You can practice the related questions from the links shared below: