General and Middle Terms in Binomial Expansion

The Binomial Expansion is an important concept of algebra that helps to expand the expressions. A Binomial is an expression with two terms. It is difficult to solve the powers manually therefore this expression makes it simpler to solve. This theorem is widely used in real-life applications in mathematics including calculus etc.

This Story also Contains

1. General Term
2. Middle Term
3. Solved Examples Based on General and Middle Terms in Binomial Expansion:

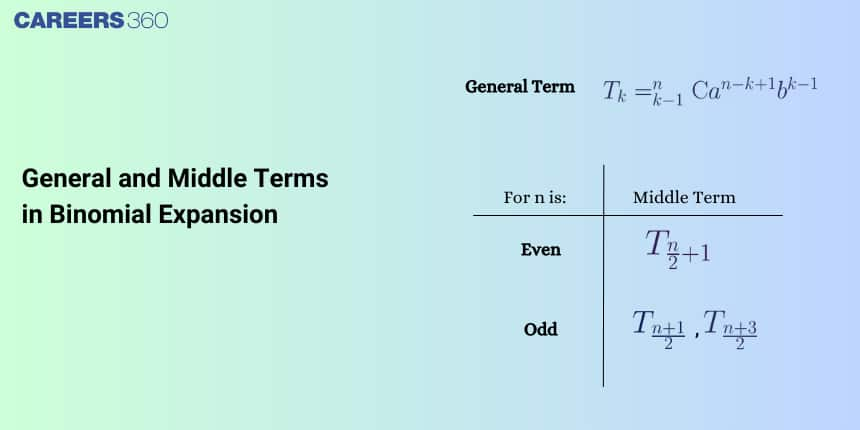
General Term

An algebraic expression consisting of only two terms is called a Binomial Expression

$
e g \cdot(a+b)^2,\left(\sqrt{x}+\frac{k}{x^2}\right)^5,(x+9 y)^{-2 / 3}
$

Sometimes we are interested only in a certain term of a binomial expansion. We do not need to fully expand a binomial to find a single specific term. $(r+1)^{\text {th }}$ term is called as general term in $(x+y)^n$ and general term is given by

$
\mathrm{T}_{\mathrm{r}+1}={ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}} {x}^{\mathrm{n}-\mathrm{r}} \cdot \mathrm{y}^{\mathrm{r}}
$

Term independent of $x$

It means a term containing $x^0$,

For example, to find term independent of x in $\left(x-\frac{1}{x}\right)^{20}$

$
\begin{aligned}
& \left(x-\frac{1}{x}\right)^{20} \\
& \Rightarrow \quad T_{r+1}={ }^{20} C_r x^{20-r}(-1)^r \frac{1}{x^r}=20 C_r x^{20-2 r}(-1)^r \\
& \Rightarrow \quad 20-2 r=0 ; r=10 \\
& \Rightarrow \quad 11^{\text {th }} \text { term is independent of } x
\end{aligned}
$

(p+1)^th term from the end

$(p+1)^{\text {th }}$ term from the end
The binomial expansion $(\mathrm{x}+\mathrm{y})^{\mathrm{n}}={ }^{\mathrm{n}} \mathrm{C}_0 \mathrm{x}^{\mathrm{n}}+{ }^{\mathrm{n}} \mathrm{C}_1 \mathrm{x}^{\mathrm{n}-1} \mathrm{y}+{ }^{\mathrm{n}} \mathrm{C}_2 \mathrm{x}^{\mathrm{n}-2} \mathrm{y}^2+\cdots+{ }^{\mathrm{n}} \mathrm{C}_{\mathrm{n}} \mathrm{y}^{\mathrm{n}}$

From Starting

$
\underbrace{{}^n C_0 x^n}_{\text{1st term}} +
\underbrace{{}^n C_1 x^{n-1} y}_{\text{2nd term}} +
\underbrace{{}^n C_2 x^{n-2} y^2}_{\text{3rd term}} + \dots +
\underbrace{{}^n C_{n-1} x y^{n-1}}_{\text{nth term}} +
\underbrace{{}^n C_n y^n}_{(n+1)\text{th term}}
$

From the End

$\underbrace{{ }^n C_0 y^n}_{\text {1st term }}+\underbrace{{ }^n C_1 y^{n-1} x}_{\text {2nd term }}+\underbrace{{ }^n C_2 y^{n-2} x^2}_{\text {3rd term }}+\cdots+\underbrace{{ }^n C_{n-1} y x^{n-1}}_{\text {nth term }}+\underbrace{{ }^n C_n x^n}_{(n+1) \text { th term }}$

(Using relation ${ }^n C_r={ }^n C_{(n-r)}$ )
Now,
Consider the binomial expansion

$
(\mathrm{y}+\mathrm{x})^{\mathrm{n}}={ }^{\mathrm{n}} \mathrm{C}_0 \mathrm{y}^{\mathrm{n}}+{ }^{\mathrm{n}} \mathrm{C}_1 \mathrm{y}^{\mathrm{n}-1} \mathrm{x}+{ }^{\mathrm{n}} \mathrm{C}_2 \mathrm{y}^{\mathrm{n}-2} \mathrm{x}^2+\cdots+{ }^{\mathrm{n}} \mathrm{C}_{\mathrm{n}} \mathrm{x}^{\mathrm{n}}
$

Just observe that, $(p+1)^{\text {th }}$ term from the end of the expansion of $(x+y)^n$ $=(p+1)^{\text {th }}$ term from the beginning of the expansion of $(y+x)^n={ }^n C_p y^{n-p}$ $x^p$

Radical Free Terms or Rational Terms

Rational term in the expansion of $\left(x^{1 / a}+y^{1 / b}\right)^N, x, y \in$ prime numbers.

First, find $T_{r+1}={ }^N C_r\left(x^{1 / a}\right)^{N-r}\left(y^{1 / b}\right)^r$

$
\therefore \quad T_{r+1}={ }^N C_r \cdot x^{(N-r) / a} \cdot y^{r / b}
$

By observation, when indices of $x$ and $y$ are integers, then the entire term will be rational

For example,

Find the number of terms in the expansion of $(\sqrt[4]{9}+\sqrt[6]{8})^{100}$ which are rational
To make x and y as prime numbers, we can rewrite the expression as

$
\therefore \text { General term, } \begin{aligned}
T_{r+1} & ={ }^{100} C_r\left(3^{1 / 2}\right)^{100-r} \cdot\left(2^{1 / 2}\right)^r \\
& ={ }^{100} C_r \cdot 3^{\frac{100-r}{2}} \cdot 2^{r / 2} \\
& ={ }^{100} C_r \cdot 3^{50-r / 2} \cdot 2^{r / 2}
\end{aligned}
$

Now, $\quad 0 \leq r \leq 100$
For $r=0,2,4,6,8, \ldots, 100$, indices of 3 and 2 are positive integers.
Hence, the number of terms which are rational $=50+1=51$

Middle Term

The middle term in the expansion $(x+y)^n$, depends on the value of ' $n$ '

Case 1 When ' $n$ ' is even
If n is even, and the number of terms in the expansion is $\mathrm{n}+1$, so $\mathrm{n}+1$ is odd number therefore only one middle term is obtained which is

$
\left(\frac{\mathrm{n}}{2}+1\right)_{\text {term. }}^{\text {th }}
$

It is given by

$
\mathrm{T}_{\frac{n}{2}+1}=\binom{n}{\frac{n}{2}} x^{\frac{n}{2}} y^{\frac{n}{2}}
$
Case 2 When ' $n$ ' is odd
In this case, the number of terms in the expansion will be $\mathrm{n}+1$. Since n is odd so, $\mathrm{n}+1$ is even. Therefore, there will be two middle terms in the expansion, namely $\left(\frac{n+1}{2}\right)^{t h}\left(\frac{n+3}{2}\right)^{t h}$ and terms. It is given by

$
T_{\frac{n+1}{2}}=\binom{n}{\frac{n-1}{2}} x^{\frac{n+1}{2}} \cdot y^{\frac{n-1}{2}} \text { and } \quad T_{\frac{n+3}{2}}=\binom{n}{\frac{n+1}{2}} x^{\frac{n-1}{2}} \cdot y^{\frac{n+1}{2}}
$

Note:

The Binomial Coefficient of the middle term is greatest among all binomial coefficients in an expansion.
- So if $n$ is even, then ${ }^n C_r$ is largest if $r=n / 2$
- And if n is odd, then ${ }^{\mathrm{n}} \mathrm{C}_{\mathrm{r}}$ is largest if $\mathrm{r}=\frac{n-1}{2}$ or $\frac{n+1}{2}$, and both these values of ${ }^n C_r$ are equal

Recommended Video Based on General and Middle Terms in Binomial Expansion:

Solved Examples Based on General and Middle Terms in Binomial Expansion:

Example 1: The sum of the real values of $x$ for which the middle term in the binomial expansion of $\left(\frac{x^3}{3}+\frac{3}{x}\right)^8$ equals 5670 is :
1) 6
2) 4
3) 0
4) 8

Solution: Middle term in Binomial Expression if n is even
$\left(\frac{n}{2}+1\right)_{\text {th term is middle term }}$
And it equals ${ }^n C_{\frac{n}{2}} \cdot x^{\frac{n}{2}} \cdot y^{\frac{n}{2}}$

Now,

The middle term can be written as

$
\begin{aligned}
& T_5={ }^8 C_4\left(\frac{x^3}{3}\right)^4\left(\frac{3}{x}\right)^4=5670 \\
& \Rightarrow 70 x^8=5670 \\
& \Rightarrow x^8=81 \\
& \Rightarrow x= \pm \sqrt{3}
\end{aligned}
$

The sum of real values $=0$
Hence, the answer is the option 3.

Example 2: In the binomial expansion of $(a-b)^n, n \geq 5$, the sum of $5^{\text {th }}$ and $6^{\text {th }}$ terms is zero, then $a / b$ equals:
1) $\frac{n-5}{6}$
2) $\frac{n-4}{5}$
3) $\frac{5}{n-4}$
4) $\frac{6}{n-5}$

Solution

As we learned in

General Term in the expansion of $(x+a)^n$

$
T_{r+1}={ }^n C_r \cdot x^{n-r} \cdot a^r
$

Now,

$
\begin{aligned}
& \text { In }(\mathrm{a}-\mathrm{b})^{\mathrm{n}} \\
& T_5={ }^n C_4(a)^{n-4}(-b)^4 \text { and } T_6={ }^n C_5(a)^{n-5}(-b)^5 \\
& \mathrm{~T}_5+\mathrm{T}_6=0 \\
& { }^n C_4(a)^{n-4}(b)^4={ }^n C_5(a)^{n-5}(b)^5 \\
& \frac{a}{b}=\frac{{ }^n C_5}{{ }^n C_4}=\frac{\frac{n!}{5!(n-5)!}}{\frac{n!}{4!(n-4)!}}=\frac{n-4}{5}
\end{aligned}
$

Hence, the answer is an option (2).

Example 3: The coefficient of $x^7$ in the expansion of $\left(1-x-x^2+x^3\right)^6$ is
1) -144
2) 132
3) 144
4) -132

Solution

As we learnt in

General Term in the expansion of $(x+a)^n$

$
T_{r+1}={ }^n C_r \cdot x^{n-r} \cdot a^r
$

Now,
We have to simplify $\left(1-x-x^2+x^3\right)^6$
We get $\left[(1-x)-x^2(1-x)\right]^6$

$
\begin{aligned}
& =\left[(1-x)\left(1-x^2\right)\right]^6 \\
& =(1-x)^6\left(1-x^2\right)^6
\end{aligned}
$

For a coefficient of $\mathrm{x}^7$ in $(1-x)^6\left(1-x^2\right)^6$

$
\begin{aligned}
& =\left(1-{ }^6 C_1 x+{ }^6 C_2 x^2 \ldots \ldots \ldots \ldots \ldots\right)\left(1-{ }^6 C_1 x^2+{ }^6 C_2 x^4-{ }^6 C_3 x^6 \ldots \ldots \ldots \ldots\right) \\
& ={ }^6 C_1 \cdot{ }^6 C_3-{ }^6 C_3 \cdot{ }^6 C_2+{ }^6 C_5 \cdot{ }^6 C_1 \\
& =120-300+36=-144
\end{aligned}
$
Hence, the answer is the option 1.

Example 4: The term independent of $x$ in expansion of $\left(\frac{x+1}{x^{2 / 3}-x^{1 / 3}+1}-\frac{x-1}{x-x^{1 / 2}}\right)^{10}$ is :
1) 310
2) 4
3) 120
4) 210

Solution

Now,

$
\begin{aligned}
& S=\left(\frac{\left(x^{1 / 3}+1\right)\left(x^{2 / 3}-x^{1 / 3}+1\right)}{\left(x^{2 / 3}-x^{1 / 3}+1\right)}-\frac{\left(x^{1 / 2}-1\right)\left(x^{1 / 2}+1\right)}{x^{1 / 2}\left(x^{1 / 2}-1\right)}\right)^{10} \\
& =\left(\left(x^{1 / 3}+1\right)-\left(1+x^{-1 / 2}\right)\right)^{10} \\
& =\left(x^{1 / 3}-x^{-1 / 2}\right)^{10} \\
& T_{r+1}={ }^{10} C_r\left(x^{1 / 3}\right)^{10-r}\left(-x^{-1 / 2}\right)^r \\
& =(-1)^r \cdot{ }^{10} C_r \cdot x^{\frac{10-r}{3}-\frac{r}{2}}
\end{aligned}
$

For term independent of $x$,

$
\Rightarrow \quad \frac{10-r}{3}-\frac{r}{2}=0 \Rightarrow 5 r=20
$

So, $T_{r+1}={ }^{10} C_4=210$
Hence, the answer is the option (4).

$x^7$ in $\left[a x^2+\left(\frac{1}{b x}\right)\right]^{11}$ equals the coefficient of $x^{-7}$ in $\left[a x-\left(\frac{1}{b x^2}\right)\right]^{11}$, if $a=1 / 2$, then $b=$
1)$1 / 2$
2)1
3) (correct)
2
4)None of these

$
\begin{aligned}
& T_{r+1} \text { of }\left(a x^2+\frac{1}{b x}\right)^{11}={ }^{11} C_r\left(a x^2\right)^{11-r}\left(\frac{1}{b x}\right)^r \\
& T_{r+1} \text { of }\left(a x-\frac{1}{b x^2}\right)^{11}={ }^{11} C_r(a x)^{11-r}\left(-\frac{1}{b x^2}\right)^r
\end{aligned}
$

$\therefore$ Coefficient of $x^7$ in $\left(a x^2+\frac{1}{b x}\right)^{11}={ }^{11} C_5 \frac{a^6}{b^5}$ and coefficient of $x^{-7}$ in $\left(a x-\frac{1}{b x^2}\right)^{11}={ }^{11} C_6 \frac{a^5}{b^6}$ Now ${ }^{11} C_5 \frac{a^6}{b^5}={ }^{11} C_6 \frac{a^5}{b^6} \quad \therefore a b=1$.

Hence, the answer is the option(3).