Hermitian matrix & Skew Hermitian Matrix

What is a Hermitian Matrix?

A Hermitian matrix is a complex square matrix that is equal to its own conjugate transpose. These matrices are widely used in linear algebra, quantum mechanics, and complex analysis. A key property is that the diagonal elements of a Hermitian matrix are always real. This section explains the definition, properties, and provides a Hermitian matrix example with detailed verification.

Definition of Hermitian Matrix

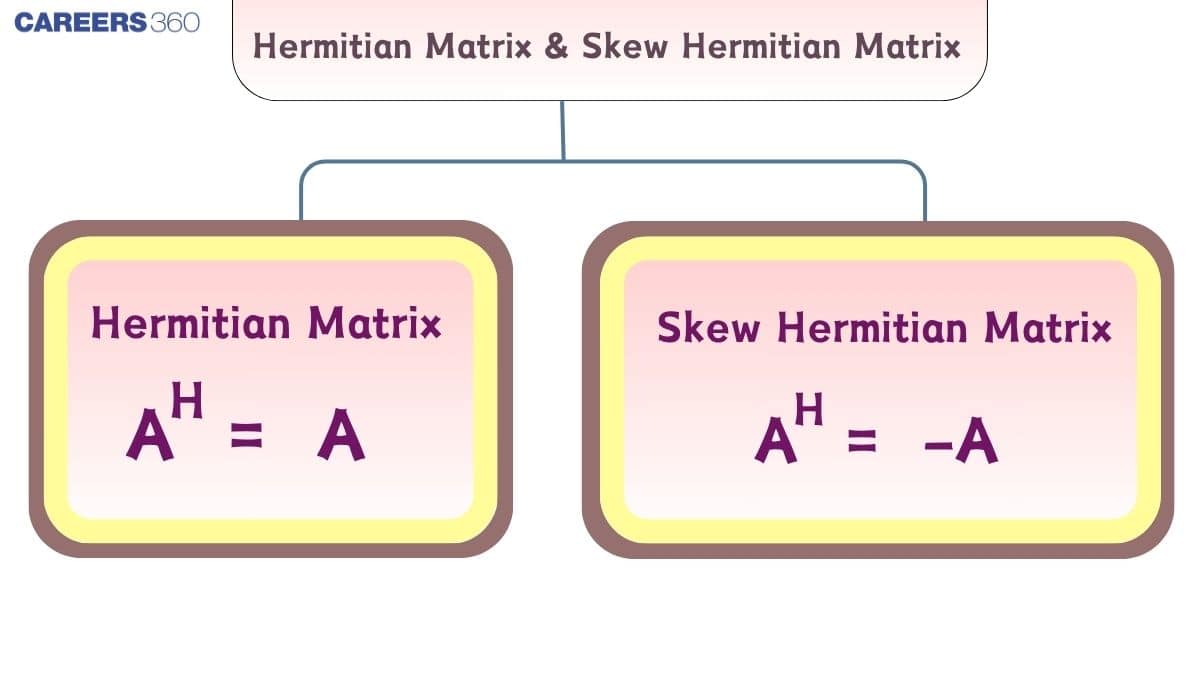
A matrix $A = [a_{ij}]$ is called a Hermitian matrix if:

$A = A^H$

where $A^H$ denotes the conjugate transpose of $A$. This condition means that:

$a_{ij} = \overline{a_{ji}}$

for all $i$ and $j$, where $\overline{a_{ji}}$ is the complex conjugate of the element at position $(j, i)$.

Properties of Hermitian Matrices

• A Hermitian matrix is always a square matrix, i.e., it has the same number of rows and columns.

• The diagonal elements of a Hermitian matrix are always real, i.e., $a_{ii} \in \mathbb{R}$.

• Off-diagonal elements satisfy $a_{ij} = \overline{a_{ji}}$.

• All eigenvalues of a Hermitian matrix are real.

• Hermitian matrices are diagonalizable by a unitary matrix.

• Hermitian matrices play a key role in representing real-valued observables in physics.

Diagonal Elements of a Hermitian Matrix

The condition $a_{ii} = \overline{a_{ii}}$ must hold for all diagonal elements. This is only possible if $a_{ii}$ is a real number. Therefore:

$\text{If } A \text{ is Hermitian, then } a_{ii} \in \mathbb{R}$

This is one of the most recognisable properties of Hermitian matrices.

Hermitian Matrix Example with Solution

Consider the matrix:

$A = \begin{bmatrix} 4 & 2 + i \\ 2 - i & 5 \end{bmatrix}$

Step 1: Find the transpose of $A$:

$A^T = \begin{bmatrix} 4 & 2 - i \\ 2 + i & 5 \end{bmatrix}$

Step 2: Take the complex conjugate of $A^T$ to get the conjugate transpose $A^H$:

$A^H = \begin{bmatrix} 4 & 2 - i \\ 2 + i & 5 \end{bmatrix}$

Step 3: Compare $A$ and $A^H$:

$A = A^H$

Therefore, $A$ is a Hermitian matrix.

We know that when we take the transpose of a matrix, its diagonal elements remain the same, and while taking conjugate we just change the sign from +ve to -ve and -ve to +ve for the imaginary part of all elements, So to satisfy the condition A' = A diagonal elements must not change, implies all diagonal element must be purely real,

e.g. Let, $A=\left[\begin{array}{ccc}3 & 3-4 i & 5+2 i \\ 3+4 i & 5 & -2+i \\ 5-2 i & -2-i & 7\end{array}\right]$
Then,

$
\begin{gathered}
\mathrm{A}^{\prime}=\left[\begin{array}{ccc}
3 & 3+4 i & 5-2 i \\
3-4 i & 5 & -2-i \\
5+2 i & -2+i & 7
\end{array}\right] \\
\therefore \mathrm{A}^H=\overline{\left(\mathrm{A}^{\prime}\right)}=\left[\begin{array}{ccc}
3 & 3-4 i & 5+2 i \\
3+4 i & 5 & -2+i \\
5-2 i & -2-i & 7
\end{array}\right]
\end{gathered}
$

here, A is Hermitian matrix as $\mathrm{A}=\mathrm{A}^H$

What is a Skew Hermitian Matrix?

A skew Hermitian matrix is a complex square matrix that satisfies a specific symmetry: it is equal to the negative of its conjugate transpose. These matrices are significant in advanced algebra, especially in fields like quantum mechanics and electrical engineering. A defining feature is that the diagonal elements of a skew Hermitian matrix are always purely imaginary or zero.

Definition of Skew Hermitian Matrix

A matrix $A$ is called a skew Hermitian matrix if:

$A = -A^H$

where $A^H$ is the conjugate transpose of $A$. This means that each element satisfies:

$a_{ij} = -\overline{a_{ji}}$

for all $i$ and $j$, where $\overline{a_{ji}}$ denotes the complex conjugate of the element in the $j^{\text{th}}$ row and $i^{\text{th}}$ column.

Properties of Skew Hermitian Matrices

• $A$ is always a square matrix.

• Diagonal elements satisfy: $a_{ii} = -\overline{a_{ii}} \Rightarrow a_{ii} \in \mathbb{C} \text{ such that } \text{Re}(a_{ii}) = 0$

So, each diagonal element is purely imaginary or zero.

• Off-diagonal elements satisfy: $a_{ij} = -\overline{a_{ji}}$

• All eigenvalues of a skew Hermitian matrix are either purely imaginary or zero.

• If $A$ is skew Hermitian, then the matrix $iA$ is Hermitian, where $i = \sqrt{-1}$.

Diagonal Elements of Skew Hermitian Matrix

For diagonal elements $a_{ii}$ in a skew Hermitian matrix:

$a_{ii} = -\overline{a_{ii}}$

This implies:

$a_{ii} + \overline{a_{ii}} = 0 \Rightarrow 2\text{Re}(a_{ii}) = 0$

Therefore, the real part of $a_{ii}$ must be zero, meaning:

$a_{ii} \in \{ bi \mid b \in \mathbb{R} \}$

So, diagonal elements are always purely imaginary or zero.

Skew Hermitian Matrix Example with Solution

Let us check whether the following matrix is skew Hermitian:

$A = \begin{bmatrix} 0 & 2+i \\ -2+i & 0 \end{bmatrix}$

Step 1: Transpose $A$:

$A^T = \begin{bmatrix} 0 & -2+i \\ 2+i & 0 \end{bmatrix}$

Step 2: Take complex conjugate:

$A^H = \begin{bmatrix} 0 & -2-i \\ 2-i & 0 \end{bmatrix}$

Step 3: Find $-A^H$:

$A^H = \begin{bmatrix} 0 & 2+i \\ -2+i & 0 \end{bmatrix}$

Since:

$A = -A^H$

The matrix is skew-Hermitian.

We know that when we take the transpose of a matrix, its diagonal elements remain the same, and while taking conjugate we just change the sign from +ve to -ve OR -ve to +ve in the imaginary part of all elements, So to satisfy the condition A? = - A, all diagonal element must be purely imaginary. As A' = - A so

$\begin{aligned} & \mathrm{a}_{\mathrm{ij}}=-\overline{\mathrm{a}_{\mathrm{ij}}} \forall \mathrm{i}, \mathrm{j} \\ & \text { if we put } \mathrm{i}=\mathrm{j} \text {, we have } \\ & \mathrm{a}_{\mathrm{ii}}=-\overline{\mathrm{a}_{\mathrm{ii}}} \Rightarrow \mathrm{a}_{\mathrm{ii}}+\overline{\mathrm{a}_{\mathrm{ii}}}=0 \\ & \Rightarrow \mathrm{a}_{\mathrm{ii}}=0\end{aligned}$

Hence all diagonal elements should be purely imaginary

e.g. Let, $\mathrm{A}=\left[\begin{array}{ccc}-3 i & -3-4 i & -5+2 i \\ 3-4 i & 5 i & i \\ 5+2 i & i & 0\end{array}\right]$
Then,

$
\begin{aligned}
\mathrm{A}^{\prime} & =\left[\begin{array}{ccc}
-3 i & 3-4 i & 5+2 i \\
-3-4 i & 5 i & i \\
-5+2 i & i & 0
\end{array}\right] \\
\therefore \mathrm{A}^\theta & =\overline{\left(\mathrm{A}^{\prime}\right)}=\left[\begin{array}{ccc}
3 i & 3+4 i & 5-2 i \\
-3+4 i & -5 i & -i \\
-5-2 i & -i & 0
\end{array}\right] \\
\quad & =-\left[\begin{array}{ccc}
-3 i & -3-4 i & -5+2 i \\
3-4 i & 5 i & i \\
5+2 i & i & 0
\end{array}\right]=-\mathrm{A}
\end{aligned}
$

Here, $A$ is Skew-Hermitian matrix as $A^\theta=-A$

Important Note:

1. For any square matrix $A$ with complex elements, the matrix $A - A^H$ is always a skew Hermitian matrix.

Proof:

Let us compute the conjugate transpose of $ A-A^H$:

$(A - A^H)^H = A^H - (A^H)^H = A^H - A = -(A - A^H)$

Hence, $A - A^H$ is skew Hermitian because:

$(A - A^H)^H = -(A - A^H)$

2. Every square matrix can be expressed as the sum of a Hermitian and a skew Hermitian matrix.

That is, if $A$ is any square matrix, then:

$A = \frac{1}{2}(A + A^H) + \frac{1}{2}(A - A^H)$

Here,

• $\frac{1}{2}(A + A^H)$ is a Hermitian matrix

• $\frac{1}{2}(A - A^H)$ is a skew Hermitian matrix

Thus, any complex square matrix can be decomposed into a Hermitian part and a skew Hermitian part.

Proofs of Properties of Hermitian and Skew-Hermitian Matrices

Understand the logical foundations behind key properties of Hermitian and Skew-Hermitian matrices. This section includes step-by-step proofs using transpose and conjugate rules, helping reinforce conceptual clarity.

i) If $A$ is a square matrix, then both $A A^H$ and $A^H A$ are Hermitian matrices.

Proof:

We check the conjugate transpose of $A A^H$:

$(A A^H)^H = (A^H)^H A^H = A A^H$

Therefore, $A A^H$ is Hermitian. Similarly,

$(A^H A)^H = (A)^H (A^H)^H = A^H A$

Hence, $A^H A$ is also Hermitian.

ii) If $A$ is a Hermitian matrix, then $i A$ is a skew Hermitian matrix, where $i = \sqrt{-1}$.

Proof:

We need to show that:

$(i A)^H = -i A$

Now,

$(i A)^H = A^H \cdot \overline{i} = A \cdot (-i) = -i A$

Since $A$ is Hermitian, $A^H = A$. Hence, $ iA$ is skew Hermitian.

iii) If $A$ is a skew Hermitian matrix, then $i A$ is a Hermitian matrix, where $i = \sqrt{-1}$.

Proof:

We need to show that:

$(i A)^H = i A$

Now, $(i A)^H = A^H \cdot \overline{i} = (-A) \cdot (-i) = i A$

Since $A$ is skew Hermitian, $A^H = -A$. Hence, $i A$ is Hermitian.

iv) If $A$ and $B$ are Hermitian matrices of the same order, then:

(a) $c A$ and $d B$ are also Hermitian, where $c, d \in \mathbb{R}$

Explanation:

If $A^H = A$ and $B^H = B$, then:

$(c A)^H = \overline{c} A^H = c A$

since $c$ is real, $\overline{c} = c$. Hence, $c A$ is Hermitian. Similarly, $d B$ is Hermitian.

Therefore,

$(c A + d B)^H = (c A)^H + (d B)^H = c A + d B$

So, $c A + d B$ is Hermitian.

(b) $A B$ is Hermitian if $A B = B A$

Proof:

Check:

$(A B)^H = B^H A^H = B A = A B$

Since $A$ and $B$ are Hermitian ($A^H = A$, $B^H = B$), and $A B = B A$, the product $A B$ is Hermitian.

(c) $A B + B A$ is Hermitian

Explanation:

From part (b), if $A B = B A$, then both $A B$ and $B A$ are Hermitian. Their sum is:

$(A B + B A)^H = (A B)^H + (B A)^H = A B + B A$

Hence, $A B + B A$ is Hermitian.

(d) $A B - B A$ is skew Hermitian

Proof:

We compute:

$(A B - B A)^H = (A B)^H - (B A)^H = B^H A^H - A^H B^H = B A - A B = - (A B - B A)$

Therefore, $A B - B A$ is skew Hermitian.

v) If $A$ and $B$ are skew Hermitian matrices of the same order, then $c A + d B$ is also skew Hermitian, where $c, d \in \mathbb{R}$

Proof:

Since $A^H = -A$ and $B^H = -B$, we have:

$(c A + d B)^H = \overline{c} A^H + \overline{d} B^H = c (-A) + d (-B) = - (c A + d B)$

Hence, $ cA + dB$ is skew Hermitian.

Difference Between Hermitian and Skew Hermitian Matrix

Solved Examples Based on Hermitian and Skew-Hermitian Matrices

Example 1: If $A$ is Hermitian such that $A^2=0$, Then

1) $A=I$

2) $\mathrm{A}=0$

3) $A^3=A$

4) none of these

Solution: Hermitian matrices –

$A^\theta = A \ \text{where } A^\theta \ \text{is the complex conjugate transpose of } A$

$A = \left[\begin{array}{cc} a & b+ic \\ b-ic & d \end{array}\right]$

$B = \left[\begin{array}{ccc} 3 & 3-4i & 5+2i \\ 3+4i & 5 & -2+i \\ 5-2i & -2-i & 2 \end{array}\right]$

$\mathrm{A} = \left[\begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots & a_{2n} \\ \ldots & \ldots & \ldots & \ldots \\ a_{n1} & a_{n2} & \ldots & a_{nn} \end{array}\right]$

$= \left[\begin{array}{cccc} \bar{a}_{11} & \bar{a}_{21} & \ldots & \bar{a}_{n1} \\ \bar{a}_{12} & \bar{a}_{22} & \ldots & \bar{a}_{n2} \\ \ldots & \ldots & \ldots & \ldots \\ \bar{a}_{1n} & \bar{a}_{2n} & \ldots & \bar{a}_{nn} \end{array}\right]$

Since $\mathrm{A}^2=0$, each element of $A A^\theta$ is zero.

$\Rightarrow \mathrm{a}_{\mathrm{i} 1} \bar{a}_{i 1}+\mathrm{a}_{\mathrm{i} 2} \bar{a}_{i 2^{+}} \ldots \ldots+\mathrm{a}_{\mathrm{in}} \bar{a}_{i n}=\left|\mathrm{a}_{\mathrm{i} 1}\right|^2+\left|\mathrm{a}_{\mathrm{i} 2}\right|^2+\ldots .+\left|\mathrm{a}_{\mathrm{in}}\right|^2=0$

$\left|a_{i 1}\right|=\left|a_{i 2}\right|=\ldots .=\left|a_{i n}\right|=0 \Rightarrow a_{i 1}=a_{i 2}=\ldots .=a_{i n}=0 \text {. Hence } A=0 \text {. }$

Hence, the correct answer is option 2.

Example 2: Find the Hermitian matrix of the matrix $A=\left[\begin{array}{ccc}3 & 4-2 i & 5+3 i \\ 4+2 i & 4 & 4+5 i \\ 5-3 i & 4-5 i & 5\end{array}\right]$

1) $A^\theta=\left[\begin{array}{ccc}3 i & -2 i & 5-3 i \\ 4+2 i & 4 & 4+5 i \\ 5+3 i & 4-5 i & 5 i\end{array}\right]$

2) $A^\theta=\left[\begin{array}{ccc}3 & 4-2 i & 5+3 i \\ 4+2 i & 4 & 4+5 i \\ 5-3 i & 4-5 i & 5\end{array}\right]$

3) $A^\theta=\left[\begin{array}{ccc}3 & 4-2 i & 5+3 i \\ 4+2 i & 4 & 4-5 i \\ 5-3 i & 4+5 i & 5\end{array}\right]$

4) $A^\theta=\left[\begin{array}{ccc}3 & 4-2 i & 5-3 i \\ 4+2 i & 4 & 4+5 i \\ 5+3 i & 4-5 i & 5\end{array}\right]$

Solution: For the matrix to be Hermitian, $A^\theta=A$
So we find $A^\theta$ and verify that it is equal to A or not
To find $A^\theta$, we first take the transpose of A and then its conjugate
So, taking the transpose of A, we have
$
A^{\prime}=\left[\begin{array}{ccc}
3 & 4+2 i & 5-3 i \\
4-2 i & 4 & 4-5 i \\
5+3 i & 4+5 i & 5
\end{array}\right]
$
Taking its conjugate now
$
\overline{\mathrm{A}^{\prime}}=\mathrm{A}^\theta=\left[\begin{array}{ccc}
3 & 4-2 i & 5+3 i \\
4+2 i & 4 & 4+5 i \\
5-3 i & 4-5 i & 5
\end{array}\right]=\mathrm{A}
$

Hence, the answer is option 2.

Example 3: Find the skew-hermitian matrix of matrix $\left[\begin{array}{ccc}i & 1-i & 2 \\ -1-i & 3 i & i \\ -2 & i & 0\end{array}\right]$.

1) $\left[\begin{array}{ccc}-i & -1+i & -2 \\ 1+i & -3 i & -i \\ 2 & -i & 0\end{array}\right]$
2) $\left[\begin{array}{ccc}i & 1-i & 2 \\ -1-i & 3 i & i \\ -2 & i & 0\end{array}\right]$
3) $\left[\begin{array}{ccc}i & -1+i & -2 \\ 1+i & 3 i & -i \\ 2 & -i & 0\end{array}\right]$
4) $\left[\begin{array}{ccc}-i & -1+i & 2 \\ 1+i & 3 i & -i \\ -2 & -i & 0\end{array}\right]$

Solution: First, we take the transpose and then it's conjugate and equate it to -A.
$
\mathrm{A}^{\prime}=\left[\begin{array}{ccc}
i & -1-i & -2 \\
1-i & 3 i & i \\
2 & i & 0
\end{array}\right]
$
now taking conjugate of the transpose
$
\overline{\mathrm{A}^{\prime}}=\left[\begin{array}{ccc}
-i & -1+i & -2 \\
1+i & -3 i & -i \\
2 & -i & 0
\end{array}\right]=-\mathrm{A}
$

Hence, the answer is the option 1.

Example 4: If $A=\left[\begin{array}{cc}2+i & 3 i \\ -3 i & x\end{array}\right]$ is a skew-Hermitian matrix, then find the value of x :
1) $2-\mathrm{i}$
2) $2+\mathrm{i}$
3) 0
4) All of these

Solution: we know that Skew hermitian matrices - $A^{\theta}=-A$

$A^{\theta}=-A$ is a complex conjugate transpose matrix of matrix $A$

since there is only restriction on the elements such as $a_{12}$ and $a_{21}$ not $a_{11}$ and $a_{22}$.

Hence, the answer is the option 4.

Example 5: Which of the following statements is true?
1) If $A$ is a hermitian matrix then, $i A$ is a skew hermitian matrix, where $i=\sqrt{-1}$
2) If $A$ is a skew-hermitian matrix then $i A$ is a hermitian matrix, where $i=\sqrt{-1}$
3) If $A$ and $B$ are hermitian matrices of the same order, then $A B-B A$ will be skew-hermitian.
4) All of the above

Solution: Let A be a matrix of order $2 \times 2$
$
A=\left[\begin{array}{cc}
a & b+i c \\
b-i c & d
\end{array}\right]
$
then $i A=\left[\begin{array}{cc}a i & b i-c \\ b i+c & d i\end{array}\right]=\left[\begin{array}{cc}a i & -c+b i \\ c+b i & d i\end{array}\right]$ which is a skew hermitian matrix.
$
\begin{aligned}
& \text{now,} \space i A=\left[\begin{array}{cc}
a i & b i-c \\
b i+c & d i
\end{array}\right]=\left[\begin{array}{cc}
a i & -c+b i \\
c+b i & d i
\end{array}\right] \\
& i^2 A=\left[\begin{array}{cc}
a i^2 & b i^2-c i \\
b i^2+c i & d i^2
\end{array}\right]=\left[\begin{array}{cc}
-a & -b-c i \\
-b+c i & -d
\end{array}\right]=-A \quad \text { which is a hermitian matrix.}
\end{aligned}
$

Thus, options 1 and 2 are true.
Let $A$ and $B$ be a hermitian matrix of order $2 \times 2$
$
A=\left[\begin{array}{cc}
a & i c \\
-i c & d
\end{array}\right] \quad B=\left[\begin{array}{cc}
e & i g \\
-i g & h
\end{array}\right]
$

Now taking transpose
$
A^{\prime}=\left[\begin{array}{cc}
a & -i c \\
i c & d
\end{array}\right] \quad B^{\prime}=\left[\begin{array}{cc}
e & -i g \\
i g & h
\end{array}\right]
$

Now taking conjugate
$
\begin{aligned}
& A^\theta=\left[\begin{array}{cc}
a & i c \\
-i c & d
\end{array}\right] \quad B^\theta=\left[\begin{array}{cc}
e & i g \\
-i g & h
\end{array}\right] \\
& A \cdot B=\left[\begin{array}{cc}
a & i c \\
-i c & d
\end{array}\right] \cdot\left[\begin{array}{cc}
e & i g \\
-i g & h
\end{array}\right] \\
& A \cdot B=\left[\begin{array}{cc}
a e+c g & i a g+i c h \\
-i e c-i d g & g c+d h
\end{array}\right] \\
& A \cdot B=\left[\begin{array}{cc}
a e+c g & i(a g+c h) \\
-i(e c+d g) & g c+d h
\end{array}\right] \\
& B \cdot A=\left[\begin{array}{cc}
e & i g \\
-i g & h
\end{array}\right] \cdot\left[\begin{array}{cc}
a & i c \\
-i c & d
\end{array}\right] \\
& B \cdot A=\left[\begin{array}{cc}
a e+g c & i e c+i g d \\
-i a g-i h c & c g+d h
\end{array}\right]
\end{aligned}
$

$
A \cdot B-B \cdot A=\left[\begin{array}{cc}
0 & i(a g+c h+e c+g d) \\
-i(e c+d g+a g+h c) & 0
\end{array}\right] \space {\text {this matrix is a skew hermitian matrix}}
$
Therefore, statement (3) is also correct
Hence, the answer is option 4.

List of Topics related to Hermitian and Skew Hermitian Matrix

Explore essential matrix concepts that complement your understanding of Hermitian and Skew Hermitian matrices. This list covers foundational definitions, operations, and matrix types, designed to build a solid base for advanced questions in Class 12 and entrance exams. Use the resources below to access notes, formulas, and solved examples for each key topic.

NCERT Resources

Explore essential NCERT resources for Class 12 Maths Chapter 3: Matrices, including detailed revision notes, fully solved NCERT textbook solutions, and exemplar problem sets. These materials help strengthen your conceptual clarity and boost exam preparation for Matrices.

Practice Questions based on Hermitian and Skew Hermitian Matrices

Sharpen your grasp of Hermitian and Skew Hermitian matrices with targeted MCQs crafted to assess key properties, definitions, and conceptual applications. These practice questions serve as a strong foundation for mastering advanced matrix concepts and are ideal for board exam prep and entrance tests.

Hermitian matrix MCQ - Practice Questions & Answers

Skew Hermitian Matrix MCQ - Practice Questions & Answers

You can practice the questions based on the next topics of matrices:

• Symmetric & Skew Symmetric Matrix MCQ - Practice Questions

• Types of Matrices MCQ - Practice Questions & Answers

• Conjugate of a Matrix MCQ - Practice Questions & Answers