Matrices
Suppose you want to organize data like marks of students in different subjects or costs of items in a store. Arranging this information neatly in rows and columns makes it easier to understand and work with. This is where matrices come into play. A matrix is a rectangular arrangement of numbers in rows and columns, which helps in solving problems in mathematics. In this article, you will learn about matrices, their types, operations, and formulas, matrix properties, and examples from class 11 and JEE mains.
This Story also Contains
- Matrix: Definition
- Order of a Matrix
- Types of Matrices
- Matrix Operations
- Inverse of a Matrix
- Trace of a Matrix
- Transpose of a Matrix
- Important Books and Resources for Matrices
- Practice Questions based on Matrices
Matrix: Definition
A matrix is a rectangular array of objects represented in rows and columns inside closed brackets [ ]. The entries of a matrix may be real or complex numbers or functions of one variable (such as polynomials, trigonometric functions or a combination of them) or more variables or any other object. Usually, matrices are denoted by capital letters A, B, C, ... etc.
General form of a matrix
If a matrix $A$ has $m$ rows and $n$ columns, then it is written as $A=\left[a_{i j}\right]_{m \times n}, 1 \leq i \leq m, 1 \leq j \leq n$.
$A=\left[a_{i j}\right]_{m \times n}=\left[\begin{array}{cccccc}a_{11} & a_{12} & \cdots & a_{1 j} & \cdots & a_{1 n} \\ a_{21} & a_{22} & \cdots & a_{2 j} & \cdots & a_{2 n} \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\ a_{i 1} & a_{i 2} & \cdots & a_{i j} & \cdots & a_{i n} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{m 1} & a_{m 2} & \cdots & a_{m j} & \cdots & a_{m n}\end{array}\right] \leftarrow$ Row 1
Order of a Matrix
The order of the matrix is the number of rows and columns of the matrix. If a matrix has ' $m$ ' rows and ' $n$ ' columns, then the order of the matrix is said to be ' $m \times n$ '.
For example, the matrix given below has $3$ rows and $4$ columns. So, the order of the matrix is $3 \times 4$ and the matrix has $12$ elements.
The order of a matrix is determined by the number of rows and columns it contains. For instance, if a matrix has "$m$" rows and "$n$" columns, its order is represented as "$m × n$".
Order of matrix = Number of row $\times$ Number of column
Examples:
1. $\left[\begin{array}{ccc}2 & 4 & -3 \\ 5 & 4 & 6\end{array}\right]$
2. $\left[\begin{array}{cc}2 & 4 i+3 \\ 5 & 4 \\ 3 i & -75\end{array}\right]$
3. $\left[\begin{array}{c}2 \\ -5 \\ 3 i \\ 71\end{array}\right]$
In the first matrix above, elements $2, 4$ and $-3$ lie in the first row and $5, 4$ and $6$ in the second row. Also, $2,$ and $5,$ lie in the first column, $4,4$ in the second column, and $-3, 6$ in the third column. Therefore, the order of a matrix is $2 \times 3$
Similarly, the Second matrix has order $3 \times 2$ and the third matrix has order $4 \times 1$
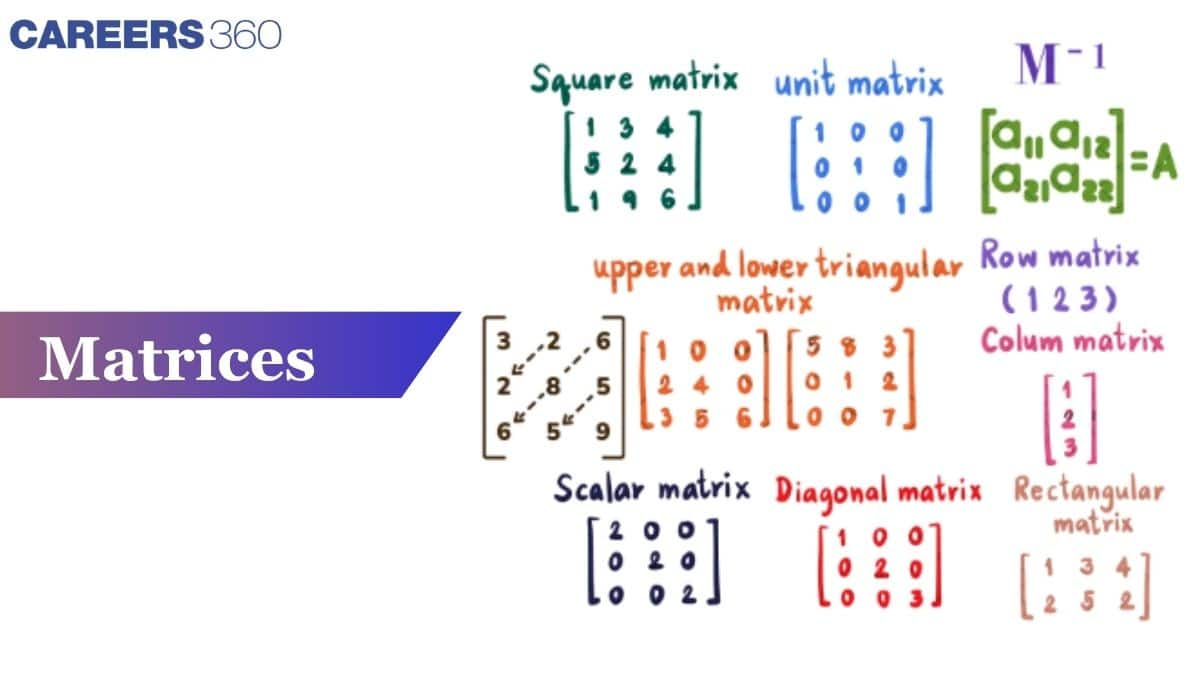
Types of Matrices
Matrices are classified based on the order of the matrices. The types of matrices are,
Row matrix: A matrix containing only one row is called a row matrix. So a matrix $A=\left[a_{i j}\right]_{m \times n}$ is said to be a row matrix when $m=1$.
It can be denoted by
$
\left[\begin{array}{llllll}
a_{11} & a_{12} & a_{13} & \ldots & \ldots & a_{1 n}
\end{array}\right]_{1 \times \mathrm{n}}
$
For example, $\left[\begin{array}{llll}1 & 32 & 81 & -32\end{array}\right]$ has only 1 row. It has order $1 \times 4$
Column matrix: A matrix containing only one column is known as a column matrix. So a matrix $A=\left[a_{i j}\right]_m \times n$ is said to be a column matrix when $n=1$. It is denoted by $\left[\begin{array}{c}a_{11} \\ a_{21} \\ a_{31} \\ \cdots \\ \cdots \\ a_{m 1}\end{array}\right]_{\mathrm{m} \times 1}$
For example, $\left[\begin{array}{c}2 \\ 32 \\ 3 \\ 7\end{array}\right]$
This matrix has order 4 x 1
Note: A matrix that contains only one row or one column is also known as a vector i.e. row vectors and column vectors.
Equal Matrices: Two matrices are said to be equal if they have the same order and each element of one matrix is equal to the corresponding elements of another matrix or we can say $a_{i j}=b_{i j}$ where $\mathrm{a}$ is the element of one matrix and $\mathrm{b}$ is the element of another matrix.
Square matrix: The square matrix is the matrix in which the number of rows $=$ number of columns. So a matrix $A=\left[a_{i j}\right]_m \times n$ is said to be a square matrix when $\mathrm{m}=\mathrm{n}$.
Example,
$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]_{3 \times 3} \text { or, }\left[\begin{array}{cc}
2 & -4 \\
7 & 3
\end{array}\right]_{2 \times 2}
$
$A+A^{\prime}$ is a symmetric matrix and $A-A^{\prime}$ is a skew-symmetric matrix for a square matrix with real number elements.
Symmetric and skew-symmetric matrix added together yields a square matrix. $1 / 2\left(A+A^{\prime}\right)+1 / 2\left(A-A^{\prime}\right)$ equals $A$.
Rectangular matrix: Rectangular matrix is the matrix in which is the number of rows $\neq$ and number of columns.
So a matrix $A=\left[a_{i j}\right] m \times n$ is said to be a rectangular matrix when $\mathrm{m} \neq \mathrm{n}$.
$
\text { For example, }\left[\begin{array}{llll}
a_{11} & a_{12} & a_{13} & a_{14} \\
a_{21} & a_{22} & a_{23} & a_{24} \\
a_{31} & a_{32} & a_{33} & a_{34}
\end{array}\right]_{3 \times 4}
$
Null matrix/ Zero Matrix: A matrix whose all elements are 0, is called a null matrix. It is represented by 'o'
$\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right] \mathrm{m} \times \mathrm{n}$, where $\mathrm{a}_{\mathrm{ij}}=0$
For example, $\left[\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right],\left[\begin{array}{llll}0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0\end{array}\right]$
Diagonal matrix: A square matrix is said to be a diagonal matrix, if all its elements except the diagonal elements are zero.
So, a matrix $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}}$ is a diagonal matrix if $\mathrm{a}_{\mathrm{ij}}=0$, whenever $\mathrm{i} \neq \mathrm{j}$ and $\mathrm{m}=\mathrm{n}$.
Diagonal matrix: $\left[\begin{array}{ccc}a_{11} & 0 & 0 \\ 0 & a_{22} & 0 \\ 0 & 0 & a_{33}\end{array}\right]$
A diagonal matrix of order $\mathrm{n} \times \mathrm{n}$ having diagonal elements as $\mathrm{d}_1, \mathrm{~d}_2, \mathrm{~d}_3 \ldots \ldots \ldots, \mathrm{d}_{\mathrm{n}}$ is denoted by $\operatorname{diag}\left[d_1, d_2, d_3 \ldots \ldots . ., d_n\right]$
For example,
$
A=\left[\begin{array}{cc}
6 & 0 \\
0 & -7
\end{array}\right] \quad B=\left[\begin{array}{ccc}
2 & 0 & 0 \\
0 & -9 & 0 \\
0 & 0 & 3
\end{array}\right]
$
so, we can write
$
\mathrm{A}=\operatorname{diag}[6,-7] \text { and } \mathrm{B}=\operatorname{diag}[2,-9,3]
$
Scalar matrix: A diagonal matrix whose all the diagonal elements are equal is called a scalar matrix.
$
A=\left[\begin{array}{ll}
3 & 0 \\
0 & 3
\end{array}\right] \quad B=\left[\begin{array}{ccc}
-3 & 0 & 0 \\
0 & -3 & 0 \\
0 & 0 & -3
\end{array}\right]
$
For a square matrix $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{n} \times \mathrm{n}}$ to be scalar matrix
$
\mathrm{a}_{\mathrm{ij}}= \begin{cases}0, & i \neq j \\ c, & i=j\end{cases}
$
Where $\mathrm{c}$ is not equal to 0
Unit or Identity Matrix: A diagonal matrix of order $\mathrm{n}$ whose all the diagonal elements are equal to one is called an identity matrix of order $\mathrm{n}$. It is represented as $I$.
So, a square matrix $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{n} \times \mathrm{n}}$ is an Identity matrix if
$
\mathrm{a}_{\mathrm{ij}}= \begin{cases}0, & i \neq j \\ 1, & i=j\end{cases}
$
For example,
$
\mathrm{I}_3=\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]
$
The product of the conjugate transpose of a unitary matrix, with the unitary matrix, gives an identity matrix.
Upper triangular matrix: A square matrix whose all elements below the principal diagonal are zero is called an upper triangular matrix.
or $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}}$ is said to be upper triangular if $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}}=0$ when $\mathrm{i}>\mathrm{j}$.
$
\text { Upper triangular matrix: }\left[\begin{array}{ccccc}
a_{11} & a_{12} & a_{13} & a_{14} & a_{15} \\
0 & a_{22} & a_{23} & a_{24} & a_{25} \\
0 & 0 & a_{33} & a_{34} & a_{35} \\
0 & 0 & 0 & a_{44} & a_{45} \\
0 & 0 & 0 & 0 & a_{55}
\end{array}\right]
$
Lower triangular matrix: A square matrix whose all elements above the principal diagonal is zero is called a lower triangular matrix.
Lower triangular matrix:
$
\left[\begin{array}{ccccc}
a_{11} & 0 & 0 & 0 & 0 \\
a_{21} & a_{22} & 0 & 0 & 0 \\
a_{31} & a_{32} & a_{33} & 0 & 0 \\
a_{41} & a_{42} & a_{43} & a_{44} & 0 \\
a_{51} & a_{52} & a_{53} & a_{54} & a_{55}
\end{array}\right]
$
Symmetric matrix: A square matrix $A=\left[a_{i j}\right]_{n \times n}$ is said to be symmetric if $A^{\prime}=A$,
$
\begin{aligned}
& \text { i.e., } \mathrm{a}_{\mathrm{ij}}=\mathrm{a}_{\mathrm{ji}} \forall \mathrm{i}, \mathrm{j} \\
& \mathrm{A}=\left[\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right] \text { then } \mathrm{A}^{\prime}=\left[\begin{array}{lll}
a & h & g \\
h & b & f \\
g & f & c
\end{array}\right]
\end{aligned}
$
Clearly, $A=A^{\prime}$, hence $A$ is a symmetric matrix
Skew-symmetric matrix: A square matrix $A=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}}$ is said to be skew-symmetric if $\mathrm{A}^{\prime}=-\mathrm{A}$
$
\text { i.e. } A^{\prime}=-A \text {, i.e., } a_{i j}=-a_{j i} \forall i, j
$
Now if we put $\mathrm{i}=\mathrm{j}$, we have
$
\begin{aligned}
& \mathrm{a}_{\mathrm{ii}}=-\mathrm{a}_{\mathrm{ii}}, \\
& \therefore 2 \mathrm{a}_{\mathrm{ii}}=0 \Rightarrow \mathrm{a}_{\mathrm{ii}}=0 \forall \mathrm{i}^{\prime} \mathrm{s}
\end{aligned}
$
Hermitian matrix: A square matrix $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right] \mathrm{n} \times \mathrm{n}$ is said to be a Hermitian matrix if $a_{i j}=\overline{a_{j i}} \forall \mathrm{i}, \mathrm{j}$,
i.e. $A=A^\theta, \quad\left[\right.$ where $A^\theta$ is conjugate transpose of matrix $\left.A\right]$
Skew-hermitian matrix: A square matrix $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right] \mathrm{n} \times \mathrm{n}$ is said to be a Skew-Hermitian matrix if $a_{i j}=-\overline{a_{i j}} \forall \mathrm{i}, \mathrm{j}$, i.e. $\mathrm{A}^\theta=-\mathrm{A}, \quad\left[\right.$ where $\mathrm{A}^\theta$ is conjugate transpose of matrix $\left.\mathrm{A}\right]$
Orthogonal matrix: A square matrix is said to be an orthogonal matrix if $A A^{\prime}=I$, where $I$ is the identity matrix.
Singular and Non-Singular matrix: A square matrix is called a singular matrix if its determinant is 0 otherwise it is called a non-singular matrix. Let's say A is a square matrix then it is singular if |A| = 0, otherwise, it will be non-singular if |A| ≠ 0.
Idempotent matrix: A square matrix is said to be an idempotent matrix if it satisfies the condition $A^2=A$
Nilpotent matrix: If $A$ satisfies the condition $Ak = 0$ and $Ak-1 ≠ 0$, then A is called a nilpotent matrix $k$ is known as the order of nilpotent matrix A.
Involutory matrix: If A satisfies the condition $A^2=A$, where $\mathrm{I}$ is the identity matrix then $\mathrm{A}$ is called the involutory matrix.
Note: $A=A^{-1}$ for involutory matrix.
Periodic matrix: If a square matrix $A$ satisfies the relation $A^{k+1}=A$, where $k$ is a +ve integer. Then $A$ is called a periodic matrix. If k is the least +ve integer for which this condition is satisfied then k is called the period of $A$.
For $k = 1$, we get $A^2=A$, which is the condition for the idempotent matrix, so the period of the idempotent matrix $=1$.
Types of Matrices: Formulae
We have provided below the list of formulae, examples of different types of matrices, so to help you understand them quickly:
| Type of Matrix | Formula / Definition | Example |
|---|---|---|
| Row Matrix | A matrix with 1 row and $n$ columns: $A = [a_{ij}]_{1 \times n}$ | $A = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix}$ |
| Column Matrix | A matrix with $m$ rows and 1 column: $A = [a_{ij}]_{m \times 1}$ | $A = \begin{bmatrix} 1 \\ 2 \\ 3 \end{bmatrix}$ |
| Square Matrix | A matrix with equal number of rows and columns: $m = n$ | $A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}$ |
| Zero or Null Matrix | All elements are zero: $a_{ij} = 0$ for all $i,j$ | $O = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}$ |
| Diagonal Matrix | Square matrix where $a_{ij} = 0$ for $i \neq j$ | $D = \begin{bmatrix} 5 & 0 \\ 0 & 7 \end{bmatrix}$ |
| Scalar Matrix | Diagonal matrix with all diagonal entries equal: $a_{ii} = k$ | $S = \begin{bmatrix} 3 & 0 \\ 0 & 3 \end{bmatrix}$ |
| Identity Matrix | Diagonal matrix with $1$s on diagonal and $0$ elsewhere: $a_{ii} = 1, a_{ij} = 0$ for $i \neq j$ | $I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}$ |
| Symmetric Matrix | Square matrix where $A = A^T$, i.e., $a_{ij} = a_{ji}$ | $A = \begin{bmatrix} 1 & 2 \\ 2 & 3 \end{bmatrix}$ |
| Skew-Symmetric Matrix | Square matrix where $A = -A^T$, i.e., $a_{ij} = -a_{ji}$ | $A = \begin{bmatrix} 0 & 2 \\ -2 & 0 \end{bmatrix}$ |
| Upper Triangular Matrix | Square matrix where $a_{ij} = 0$ for all $i > j$ | $U = \begin{bmatrix} 1 & 3 \\ 0 & 2 \end{bmatrix}$ |
| Lower Triangular Matrix | Square matrix where $a_{ij} = 0$ for all $i < j$ | $L = \begin{bmatrix} 1 & 0 \\ 4 & 2 \end{bmatrix}$ |
Matrix Operations
The addition, subtraction, and multiplication of matrices are the basic algebraic matrix operations.
Addition of matrices
Two matrices can be added only when they are of the same order
If two matrices of $A$ and $B$ are of the same order, they are said to be conformable for addition.
If $A$ and $B$ are matrices of order $m \times n$, then their sum will also be a matrix of the same order and in addition, corresponding elements of $ A$ and $B$ get added.
So if $A=\left[a_{i j}\right]_{m \times n}, B=\left[b_{i j}\right]_{m \times n}$ Then, $A+B=\left[a_{i j}+b_{i j}\right]_{m \times n}$ for all $\mathrm{i}, \mathrm{j}$
Example:
$
\begin{aligned}
\mathrm{A} & =\left[\begin{array}{lll}
10 & 20 & 30 \\
20 & 30 & 40 \\
30 & 40 & 50
\end{array}\right], \quad \mathrm{B}=\left[\begin{array}{lll}
50 & 40 & 30 \\
40 & 30 & 20 \\
30 & 20 & 10
\end{array}\right] \\
\mathrm{A}+\mathrm{B} & =\left[\begin{array}{lll}
10+50 & 20+40 & 30+30 \\
20+40 & 30+30 & 40+20 \\
30+30 & 40+20 & 50+10
\end{array}\right]=\left[\begin{array}{lll}
60 & 60 & 60 \\
60 & 60 & 60 \\
60 & 60 & 60
\end{array}\right]
\end{aligned}
$
Subtraction of matrices
Two matrices can be subtracted only when they are of the same order. If $A$ and $B$ are matrices of order $m \times n$ then their difference will also be a matrix of the same order and in subtraction, corresponding elements of $A$ and $B$ get subtracted. So if
$
\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}}, \mathrm{B}=\left[\mathrm{b}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}} \text { Then, } \mathrm{A}-\mathrm{B}=\left[\mathrm{a}_{\mathrm{ij}}-\mathrm{b}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n} \text { for all } \mathrm{i}, \mathrm{j}}
$
Example:
$
\begin{aligned}
\mathrm{A} & =\left[\begin{array}{lll}
10 & 20 & 30 \\
20 & 30 & 40 \\
30 & 40 & 50
\end{array}\right], \quad \mathrm{B}=\left[\begin{array}{lll}
50 & 40 & 30 \\
40 & 30 & 20 \\
30 & 20 & 10
\end{array}\right] \\
\mathrm{A}-\mathrm{B} & =\left[\begin{array}{lll}
10-50 & 20-40 & 30-30 \\
20-40 & 30-30 & 40-20 \\
30-30 & 40-20 & 50-10
\end{array}\right]=\left[\begin{array}{ccc}
-40 & -20 & 0 \\
-20 & 0 & 20 \\
0 & 20 & 40
\end{array}\right]
\end{aligned}
$
Scalar multiplication
Let $\mathrm{k}$ be any scalar number, and $A=\left[a_{i j}\right]_{m \times n}$ be a matrix. Then the matrix is obtained by multiplying every element $\mathrm{A}$ by a scalar $\mathrm{k}$ and denoted as $kA$.
$
\begin{aligned}
& k A=\left[k a_{i j}\right]_{m \times n} \\
& \qquad \mathrm{~A}=\left[\begin{array}{ll}
2 & 6 \\
3 & 7 \\
5 & 8
\end{array}\right] \text { then, } 3 \mathrm{~A}=\left[\begin{array}{ll}
3 \times 2 & 3 \times 6 \\
3 \times 3 & 3 \times 7 \\
3 \times 5 & 3 \times 8
\end{array}\right]=\left[\begin{array}{cc}
6 & 18 \\
9 & 21 \\
15 & 24
\end{array}\right]
\end{aligned}
$
Properties of scalar multiplication
If $A$ and $B$ are two matrices and $k, l$ are scalar then
i) $k(A+B)=k A+k B$
ii) $k(A)=k(I A)=l(k A)$
iii) $(k+1) A=k A+1 A$
iv) $(-k) A=-(k A)=k(-A)$
v) $1 \mathrm{~A}=\mathrm{A},(-1) \mathrm{A}=-\mathrm{A}$
Note: $A$ and $B$ have the same order $m \times n$.
Now lets see how to multiply two matrices.
Multiplication of Matrices
Product of two matrices $A$ and $B$ can be found if the number of columns in matrix $ A$ and the number rows in matrix $B$ are equal. Otherwise, multiplication of matrices is not possible.
i) $A B$ is defined only if $\operatorname{col}(A)=\operatorname{row}(B)$
ii) $B A$ is defined only if $\operatorname{col}(B)=\operatorname{row}(A)$
If
$\begin{aligned} & \mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}} \\ & \mathrm{B}=\left[\mathrm{b}_{\mathrm{ij}}\right]_{\mathrm{n} \times \mathrm{p}} \\ & \mathrm{C}=\mathrm{AB}=\left[\mathrm{c}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{p}} \\ & \text { Where } c_{\mathrm{ij}}=\sum_{\mathrm{j}=1}^{\mathrm{n}} \mathrm{a}_{\mathrm{ij}} \mathrm{b}_{\mathrm{jk}}, 1 \leq \mathrm{i} \leq \mathrm{m}, 1 \leq \mathrm{k} \leq \mathrm{p} \\ & =a_{i 1} b_{1 k}+a_{i 2} b_{2 k}+a_{i 3} b_{3 k}+\ldots+a_{i n} b_{n k} \\ & \end{aligned}$
For example
Suppose, two matrices are given
$
\mathrm{A}=\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{33}
\end{array}\right]_{2 \times 3} \quad \text { and } \quad \mathrm{B}=\left[\begin{array}{lll}
b_{11} & b_{12} & b_{13} \\
b_{21} & b_{22} & b_{23} \\
b_{31} & b_{32} & b_{33}
\end{array}\right]_{3 \times 3}
$
To obtain the entries in row $i$ and column j of AB, we multiply the entries in row $i$ of $\mathrm{A}$ by column $j$ in $\mathrm{B}$ and add.
given matrices $\mathrm{A}$ and $\mathrm{B}$, where the order of $\mathrm{A}$ are $2 \times 3$ and the order of $\mathrm{B}$ are $3 \times 3$, the product of $\mathrm{AB}$ will be a $2 \times 3$ matrix.To obtain the entry in row 1, column 1 of $\mathrm{AB}$, multiply the first row in $\mathrm{A}$ by the first column in $\mathrm{B}$, and add.
$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13}
\end{array}\right]\left[\begin{array}{l}
b_{11} \\
b_{21} \\
b_{31}
\end{array}\right]=\mathrm{a}_{11} \cdot \mathrm{b}_{11}+\mathrm{a}_{12} \cdot \mathrm{b}_{21}+\mathrm{a}_{13} \cdot \mathrm{b}_{31}
$
To obtain the entry in row 1, column 2 of $\mathrm{AB}$, multiply the first row in $\mathrm{A}$ by the second column in B and add.
$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13}
\end{array}\right]\left[\begin{array}{l}
b_{12} \\
b_{22} \\
b_{32}
\end{array}\right]=\mathrm{a}_{11} \cdot \mathrm{b}_{12}+\mathrm{a}_{12} \cdot \mathrm{b}_{22}+\mathrm{a}_{13} \cdot \mathrm{b}_{32}
$
To obtain the entry in row 1, column 3 of $\mathrm{AB}$, multiply the first row in $A$ by the third column in B, and add.
$
\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13}
\end{array}\right]\left[\begin{array}{l}
b_{13} \\
b_{23} \\
b_{33}
\end{array}\right]=\mathrm{a}_{11} \cdot \mathrm{b}_{13}+\mathrm{a}_{12} \cdot \mathrm{b}_{23}+\mathrm{a}_{13} \cdot \mathrm{b}_{33}
$
We proceed the same way to obtain the second row of $\mathrm{AB}$. In other words, row 2 of $\mathrm{A}$ times column 1 of $\mathrm{B}$; row 2 of A times column 2 of B; row 2 of A times column 3 of B.
When complete, the product matrix will be
$
\mathrm{AB}=\left[\begin{array}{lll}
a_{11} \cdot b_{11}+a_{12} \cdot b_{21}+a_{13} \cdot b_{31} & a_{11} \cdot b_{12}+a_{12} \cdot b_{22}+a_{13} \cdot b_{32} & a_{11} \cdot b_{13}+a_{12} \cdot b_{23}+a_{13} \cdot b_{33} \\
a_{21} \cdot b_{11}+a_{22} \cdot b_{21}+a_{23} \cdot b_{31} & a_{21} \cdot b_{12}+a_{22} \cdot b_{22}+a_{23} \cdot b_{32} & a_{21} \cdot b_{13}+a_{22} \cdot b_{23}+a_{23} \cdot b_{33}
\end{array}\right]
$
Matrix Multiplication Rules
The following matrix multiplication rules and properties can be expressed using the above-described formula and process.
- If the number of rows in $B$ equals the number of columns in $A$, then the product of two matrices $A$ and $B$ is defined.
- BA does not need to be defined if $AB$ is defined.
- Both $AB$ and $BA$ are defined if $A$ and $B$ are square matrices of the same order.
- It is not required for $AB$ to equal $BA$ if both $AB$ and $BA$ are defined.
- One of the matrices is not required to be a zero matrix in order for the product of two matrices to be a zero matrix.
Properties of Matrix Multiplication
i) Multiplication may or may not be commutative, so $AB$ may or may not be equal to $BA$
ii) Matrix multiplication is associative, meaning $A(B C)=(A B) C$
iii) Matrix multiplication is distributive over addition, mean $A(B+C)=A B+A C$ and $(B+C) A=B A+C A$
iv) If matrix multiplication of two matrices gives a null matrix then it doesn't mean that any of those two matrices was a null matrix.
$A=\left[\begin{array}{ll}0 & 2 \\ 0 & 0\end{array}\right]$ and $B=\left[\begin{array}{ll}1 & 0 \\ 0 & 0\end{array}\right]$, then $A B=\left[\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right]$
v) Cancellation law in matrix multiplication doesn't hold, which means $A B=A C \Rightarrow B$ $=\mathrm{C}$
vi) Matrix multiplication $A \times A$ is represented by $A^2$. Thus, $A \cdot A \cdot A \cdot A$ .........$n$ times $=A^n$.
vii) if $\mathrm{A}$ is $\mathrm{m} \times \mathrm{n}$ matrix then, $\mathrm{I}_{\mathrm{m}} \mathrm{A}=\mathrm{A}=\mathrm{AI}_{\mathrm{n}}$.
Inverse of a Matrix
A non-singular square matrix $A$ is said to be invertible if there exists a non-singular square matrix $B$ such that $
\mathrm{AB}=\mathrm{I}=\mathrm{BA}
$ and the matrix $B$ is called the inverse of matrix $A$. Clearly, $B$ should also have the same order as $A$.
Hence, $\mathrm{A}^{-1}=\mathrm{B} \Leftrightarrow \mathrm{AB}=\mathbb{I}_{\mathrm{n}}=\mathrm{BA}$
The inverse of a $2 \times 2$ Matrix
Let $A$ is a square matrix of order $2$
$
\mathrm{A}=\left[\begin{array}{ll}
a & b \\
c & d
\end{array}\right]
$
Then,
$
\mathrm{A}^{-1}=\frac{1}{\mathrm{ad}-\mathrm{bc}}\left[\begin{array}{cc}
d & -b \\
-c & a
\end{array}\right]
$
The inverse of a $3 \times 3$ Matrix
The inverse of $3 \times 3$ Matrix can be caluculated by the formula $A^{-1}=\frac{1}{|A|} \cdot \operatorname{adj}(A)$
Trace of a Matrix
The sum of all diagonal elements of a square matrix is called the trace of a matrix. Lying along the principal diagonal is called the trace of $A.$
The trace of the matrix is denoted by $Tr(A)$ or $tr.A$.
$
\operatorname{Tr}(\mathrm{A})=\sum_{\mathrm{i}=1}^{\mathrm{n}} \mathrm{a}_{\mathrm{ii}}
$
Let us consider the square matrix of order $3 \times 3$ as shown below. The elements of the matrix are $a_{11}, a_{12}, a_{13}$ $\qquad$ , $a_{33}$. The principal diagonal elements are $a_{11}, a_{22}, a_{33}$. So trace of the matrix is the sum of all principal diagonal elements.
$
\begin{aligned}
& A=\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right] \\
& \operatorname{Tr}(A)=a_{11}+a_{22}+a_{33}
\end{aligned}
$
e.g. For a given matrix $\mathrm{A}$,
$
A=\left[\begin{array}{ccc}
-2 & 4 & 7 \\
8 & 3 & -1 \\
5 & -6 & 9
\end{array}\right], \operatorname{Tr}(\mathrm{A})=-2+3+9=10
$
Transpose of a Matrix
A matrix can be transposed by interchanging its rows into columns or its columns into rows. The letter "$T$" in the superscript of the matrix is used to denote the transpose of the matrix.
In simple language, the transpose of a matrix is changing its rows into columns or columns into rows.
Let $\mathrm{A}=\left[\mathrm{a}_{\mathrm{ij}}\right]_{\mathrm{m} \times \mathrm{n}}$ be a matrix, then matrix obtained by changing rows into columns or vice-versa will give transpose of $\mathrm{A}$ which is denoted as $\mathrm{A}^{\prime}$ or $\mathrm{A}^{\top}$. Hence $\mathrm{A}^{\prime}=\left[\mathrm{a}_{\mathrm{ji}}\right]_{\mathrm{n} \times \mathrm{m}}$
$
\mathrm{A}=\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right] \Rightarrow \mathrm{A}^{\prime}=\left[\begin{array}{lll}
a_{11} & a_{21} & a_{31} \\
a_{12} & a_{22} & a_{32} \\
a_{13} & a_{23} & a_{33}
\end{array}\right]
$
Example: If, $A=\left[\begin{array}{ll}2 & 6 \\ 3 & 7 \\ 5 & 8\end{array}\right]$ then, $A^{\prime}=\left[\begin{array}{lll}2 & 3 & 5 \\ 6 & 7 & 8\end{array}\right]$
Properties of Transpose of a Matrix
If $A^{\prime}$ and $B^{\prime}$ denote the transpose of matrices $A$ and $B$ respectively, then the properties of transpose are:
i) Transpose of the Transpose: Taking the transpose of the transpose matrix returns the original matrix. Hence, $\left(A^{\prime}\right)^{\prime} = A$.
ii) Transpose of Sum or Difference: The transpose of the addition or subtraction of two matrices $A$ and $B$ equals the sum or difference of their transposes.
That is, $(A \pm B)^{\prime} = A^{\prime} \pm B^{\prime}$, provided $A$ and $B$ have conformable dimensions.
iii) Transpose of Scalar Multiplication: The transpose of a scalar multiplied by a matrix is the scalar multiplied by the transpose of the matrix.
Formally, $(kA)^{\prime} = k A^{\prime}$ for any scalar $k$.
iv) Transpose of Product: The transpose of the product of two matrices equals the product of their transposes in reverse order.
In other words, $(AB)^{\prime} = B^{\prime} A^{\prime}$, where $A$ and $B$ are conformable for multiplication.
These properties are fundamental in matrix algebra and widely used in linear transformations, simplifying computations and proofs involving matrices.
List of topics related to matrices according to NCERT/JEE MAIN
Explore the essential topics on matrices as prescribed by NCERT and required for JEE MAIN preparation. This includes matrix types, operations, properties, determinants, inverse, and applications in solving linear equations.
Important Books and Resources for Matrices
Check below recommended books and study materials that cover matrices comprehensively, aiding in concept clarity and providing ample practice for school exams and competitive tests like JEE.
| Book Title | Author / Publisher | Description |
|---|---|---|
| NCERT Class 12 Mathematics | NCERT | Official textbook with clear explanations and examples on Matrices. |
| Higher Algebra | Hall & Knight | Comprehensive coverage of matrices and related algebraic concepts. |
| Matrices - Arihant Publications | Arihant | Focused on concept clarity and practice for board and competitive exams. |
| Problems in Algebra | V.L. Malakhov | Collection of problems and solutions for in-depth practice on matrices. |
NCERT Resources
Access well-structured NCERT notes, solutions, and exemplar problems for matrices, designed to simplify learning and ensure thorough understanding of this important chapter.
NCERT Maths Notes for Class 12th Chapter 3 - Matrices
NCERT Maths Solutions for Class 12th Chapter 3 - Matrices
NCERT Maths Exemplar Solutions for Class 12th Chapter 3 - Matrices
NCERT Subjectwise Resources
Find organized NCERT study materials subject-wise, offering detailed chapter-wise notes and practice resources to help in effective exam preparation.
| Resource | Mathematics | Physics | Chemistry |
|---|---|---|---|
| NCERT Notes | NCERT notes Class 12 Maths | NCERT notes Class 12 Physics | NCERT notes Class 12 Chemistry |
| NCERT Solutions | NCERT solutions for Class 12 Mathematics | NCERT solutions for Class 12 Physics | NCERT solutions for Class 12 Chemistry |
Practice Questions based on Matrices
Practice a variety of questions on matrices to strengthen problem-solving skills and boost exam readiness. Regular practice helps build confidence and mastery of concepts.
Frequently Asked Questions (FAQs)
A $2 \times 2$ matrix in maths is a square matrix consisting of 4 elements with $2$ rows and $2$ columns.
A matrix is a rectangular array of numbers arranged in rows and columns. It is used to organize data and solve systems of linear equations efficiently.
Two matrices can be added or subtracted only if they have the same dimensions. Corresponding elements are added or subtracted to form a new matrix.
A symmetric matrix is equal to its transpose, meaning the element in the $i^\text{th}$ row and $j^\text{th}$ column is the same as in the $j^\text{th}$ row and $i^\text{th}$ column.
A square matrix is called a singular matrix if its determinant is 0 otherwise it is called a non-singular matrix. Let's say A is a square matrix then it is singular if |A| = 0, otherwise, it will be non-singular if |A| ≠ 0.
The inverse matrix of $2 \times 2$ matrix is $
\mathrm{A}^{-1}=\frac{1}{\mathrm{ad}-\mathrm{bc}}\left[\begin{array}{cc}
d & -b \\
-c & a
\end{array}\right]
$.
The inverse of $3 \times 3$ Matrix can be caluculated by the formula $A^{-1}=\frac{1}{|A|} \cdot \operatorname{adj}(A)$