Adjoint and Inverse of a Matrix

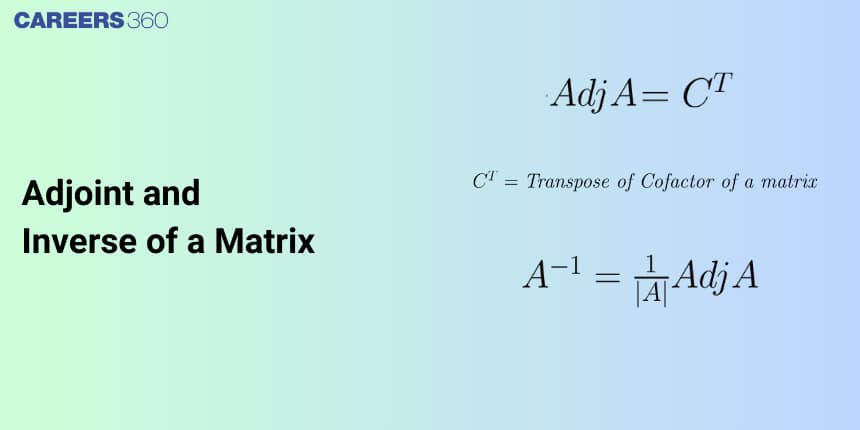
Adjoint of a Matrix

The adjoint of a matrix is obtained by taking the transpose of the cofactor matrix of a given square matrix $A$. If $A = [a_{ij}]{n \times n}$, then each cofactor $C{ij}$ is calculated by removing the $i^{th}$ row and $j^{th}$ column and finding the determinant of the remaining matrix, multiplied by $(-1)^{i+j}$.

In simple words, adjoint of a matrix A is the transpose of the cofactor matrix of the matrix A. A Cofactor matrix of matrix A is a matrix that has the same order as that of A and has elements in place of $a_{i j}$
$
\text { let } A=\left[\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right]
$
and let the cofactor of every element is
$
\left[\begin{array}{lll}
C_{11} & C_{12} & C_{13} \\
C_{21} & C_{22} & C_{23} \\
C_{31} & C_{32} & C_{33}
\end{array}\right]
$
then Adjoint of $\mathrm{A}$ is
$
A^{\prime}=\left[\begin{array}{lll}
C_{11} & C_{12} & C_{13} \\
C_{21} & C_{22} & C_{23} \\
C_{31} & C_{32} & C_{33}
\end{array}\right]^{\prime}=\left[\begin{array}{lll}
C_{11} & C_{21} & C_{31} \\
C_{12} & C_{22} & C_{32} \\
C_{13} & C_{23} & C_{33}
\end{array}\right]
$

Steps to Find Adjoint of a Matrix

1. Cofactor Matrix

For a square matrix $A = [a_{ij}]$, the cofactor matrix is

$C = [C_{ij}], \quad \text{where } C_{ij} = (-1)^{i+j} \cdot M_{ij}$

Here, $M_{ij}$ is the minor of element $a_{ij}$ (determinant of the sub-matrix formed by deleting the $i^{th}$ row and $j^{th}$ column).

2. Transpose of Cofactor Matrix

The adjoint matrix is obtained by transposing the cofactor matrix:

$\text{Adj}(A) = C^T$

Formula for Adjoint of a Matrix

The general formula is:

$\text{Adj}(A) = [C_{ij}]^T$

This means we first calculate cofactors $C_{ij}$, then take the transpose to form the adjoint.

Example of Finding Adjoint of a Matrix

Let $A = \begin{bmatrix} 1 & 2 & 3 \\ 0 & 4 & 5 \\ 1 & 0 & 6 \end{bmatrix}$

Step 1: Find Cofactors

$C_{11} = \begin{vmatrix} 4 & 5 \\ 0 & 6 \end{vmatrix} = 24, \quad C_{12} = -\begin{vmatrix} 0 & 5 \\ 1 & 6 \end{vmatrix} = 5, \quad C_{13} = \begin{vmatrix} 0 & 4 \\ 1 & 0 \end{vmatrix} = -4$

Similarly,

$C_{21} = -\begin{vmatrix} 2 & 3 \\ 0 & 6 \end{vmatrix} = -12, \quad C_{22} = \begin{vmatrix} 1 & 3 \\ 1 & 6 \end{vmatrix} = 3, \quad C_{23} = -\begin{vmatrix} 1 & 2 \\ 1 & 0 \end{vmatrix} = 2$

$C_{31} = \begin{vmatrix} 2 & 3 \\ 4 & 5 \end{vmatrix} = -2, \quad C_{32} = -\begin{vmatrix} 1 & 3 \\ 0 & 5 \end{vmatrix} = -5, \quad C_{33} = \begin{vmatrix} 1 & 2 \\ 0 & 4 \end{vmatrix} = 4$

So the cofactor matrix is:

$C = \begin{bmatrix} 24 & 5 & -4 \\ -12 & 3 & 2 \\ -2 & -5 & 4 \end{bmatrix}$

Step 2: Transpose Cofactor Matrix

$\text{Adj}(A) = C^T = \begin{bmatrix} 24 & -12 & -2 \\ 5 & 3 & -5 \\ -4 & 2 & 4 \end{bmatrix}$

Thus, the adjoint of $A$ is:

$\text{Adj}(A) = \begin{bmatrix} 24 & -12 & -2 \\ 5 & 3 & -5 \\ -4 & 2 & 4 \end{bmatrix}$

Properties of the adjoint of a matrix

1. If A is a square matrix of order n, then

$(\operatorname{Adj} \mathrm{A}) \mathrm{A}=\mathrm{A}(\operatorname{Adj} \mathrm{A})=|\mathrm{A}| \mathbb{I}_{\mathrm{n}}$, or product of a matrix, and its adjoint is commutative.
Proof: Let, $\mathrm{A}=\left[\begin{array}{lll}a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33}\end{array}\right]$, then adj $\mathrm{A}=\left[\begin{array}{lll}A_{11} & A_{21} & A_{31} \\ A_{12} & A_{22} & A_{32} \\ A_{13} & A_{23} & A_{33}\end{array}\right]$ where, $A_{i j}$ is co - factor of $a_{i j}$

Since the sum of the product of elements of a row (or a column) with corresponding cofactors is equal to $|\mathrm{A}|$ and otherwise zero, we have
$
\mathrm{A}(\operatorname{adj} \mathrm{A})=\left[\begin{array}{ccc}
|A| & 0 & 0 \\
0 & |A| & 0 \\
0 & 0 & |A|
\end{array}\right]=|\mathrm{A}|\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]=|\mathrm{A}| \mathrm{I}
$

If $A$ is a singular matrix of order $n$, then $(\operatorname{Adj} A) A=A(\operatorname{Adj} A)=0$ (null matrix) $\quad(A s|A|=0$ )
2. If $A$ is a non-singular square matrix of order $n$, then $|A d j A|=|A|^{n-1}$

Proof:
$
A(\operatorname{Adj} A)=|A| I_n
$

Taking determinants on both sides
$
\begin{aligned}
& |\mathrm{A}(\operatorname{Adj} \mathrm{A})|=|| \mathrm{A}\left|\mathrm{I}_{\mathrm{n}}\right| \\
& |\mathrm{A}||(\operatorname{Adj} \mathrm{A})|=|\mathrm{A}|^{\mathrm{n}}
\end{aligned}
$

$
|(\operatorname{adj} \mathrm{A})|=|\mathrm{A}|^{\mathrm{n}-1}
$
3. If $A$ and $B$ are square matrices of order $n$, then, $\operatorname{adj}(A B)=(\operatorname{adj} B)(\operatorname{adj} A)$
4. If $\mathrm{A}$ is a square matrix of order $\mathrm{n}$, then, $(\operatorname{adj} \mathrm{A})^{\prime}=\operatorname{adj} \mathrm{A}^{\prime}$
5. If $\mathrm{A}$ is a square a non-singular matrix of order $\mathrm{n}$, then $\operatorname{adj}(\operatorname{adj} \mathrm{A})=|\mathrm{A}|^{\mathrm{n}-2} \mathrm{~A}$

Proof:
$A(\operatorname{adj} A)=|A| \mathbb{I}_n$
replace $\mathrm{A}$ by $\operatorname{adj} \mathrm{A}$, then
$(\operatorname{adj} \mathrm{A})(\operatorname{adj}(\operatorname{adj} \mathrm{A}))=|\operatorname{adj} A| \mathbb{I}_{\mathrm{n}}=|\mathrm{A}|^{\mathrm{n}-1} \mathbb{I}_{\mathrm{n}}$
Pre - multiplying both sides by matrix $\mathrm{A}$, then
$\mathrm{A}(\operatorname{adj} \mathrm{A})(\operatorname{adj}(\operatorname{adj} \mathrm{A}))=\mathrm{A} \mathbb{I}_{\mathrm{n}}|\mathrm{A}|^{\mathrm{n}-1}=\mathrm{A}|\mathrm{A}|^{\mathrm{n}-1}$
$|\mathrm{A}| \mathbb{I}_{\mathrm{n}}(\operatorname{adj}(\operatorname{adj} \mathrm{A}))=\mathrm{A}|\mathrm{A}|^{\mathrm{n}-1}$
$(\operatorname{adj}(\operatorname{adj} A))=A|A|^{\mathrm{n}-2}=|\mathrm{A}|^{\mathrm{n}-2} \mathrm{~A}$
6. If $\mathrm{A}$ is a non-singular square matrix, then, $|\operatorname{adj}(\operatorname{adj} \mathrm{A})|=|\mathrm{A}|^{(\mathrm{n}-1)^2}$

Proof: from the previous property, we know that
$
\operatorname{adj}(\operatorname{adj} \mathrm{A})=|\mathrm{A}|^{(\mathrm{n}-2)} \mathrm{A}
$

Taking determinants on both sides,
$
|\operatorname{adj}(\operatorname{adj} \mathrm{A})|=\left.\left.|| \mathrm{A}\right|^{(\mathrm{n}-2)} \mathrm{A}|=| \mathrm{A}\right|^{\mathrm{n}(\mathrm{n}-2)}|\mathrm{A}|=|\mathrm{A}|^{(\mathrm{n}-1)^2}
$
(using $|k A|=k^n|A|$ )
7. If $A$ is a square matrix of order $n$ and $m$ is any natural number, then $\left(\operatorname{adj} A^m\right)=(\operatorname{adj} A)^m$
8. If $A$ is a square matrix of order $n$ and $k$ is a scalar, then, $\operatorname{adj}(k A)=k^{n-1} \cdot(\operatorname{adj} A)$

The inverse of a Matrix

The inverse of a matrix is a special matrix that, when multiplied with the original square matrix $A$, gives the identity matrix. If $A$ is a square matrix of order $n$, then its inverse is denoted by $A^{-1}$, and it satisfies:

$A \cdot A^{-1} = A^{-1} \cdot A = I_n$

where $I_n$ is the identity matrix of order $n$.

A non-singular square matrix A is said to be invertible if there exists a non-singular square matrix B such that

$AB = I = BA $

and the matrix B is called the inverse of matrix A. Clearly, B should also have the same order as A.

Hence, $\mathrm{A}^{-1}=\mathrm{B} \Leftrightarrow \mathrm{AB}=\mathbb{I}_{\mathrm{n}}=\mathrm{BA}$
The formula for the inverse of $\mathrm{A}$
We know
$
\begin{aligned}
& \mathrm{A}(\operatorname{adjA})=|\mathrm{A}| \mathbb{I}_{\mathrm{n}} \\
& \text { Multiplying both sides by } \mathrm{A}^{-1} \\
& \Rightarrow \mathrm{A}^{-1} \mathrm{~A}(\operatorname{adj} \mathrm{A})=\mathrm{A}^{-1} \mathbb{I}_{\mathrm{n}}|\mathrm{A}| \\
& \Rightarrow \mathbb{I}_{\mathrm{n}}(\operatorname{adjA})=\mathrm{A}^{-1}|\mathrm{~A}| \mathbb{I}_{\mathrm{n}} \quad\left(\text { As } A^{-1} \cdot A=I\right) \\
& \mathrm{A}^{-1}=\frac{\operatorname{adj} \mathrm{A}}{|\mathrm{A}|}
\end{aligned}
$

Hence, $\mathrm{A^{-1} = B \Leftrightarrow AB = \mathbb{I}_n = BA}$

The formula for the inverse of A is $ \mathrm{A}^{-1}=\frac{\operatorname{adj} \mathrm{A}}{|\mathrm{A}|}$ .

Properties of Inverse Matrix

The inverse of a matrix has several important properties that are widely used in linear algebra, matrix equations, and transformations:

1. Inverse of Identity Matrix

   $I^{-1} = I$

   The identity matrix is its own inverse.

2. Inverse of an Inverse

   $(A^{-1})^{-1} = A$

   Taking inverse twice gives back the original matrix.

3. Inverse of a Product of Matrices

   $(AB)^{-1} = B^{-1} A^{-1}$

   (Order reverses while finding the inverse of a product).

4. Inverse of a Transpose

   $(A^T)^{-1} = (A^{-1})^T$

   The inverse of a transpose is equal to the transpose of the inverse.

5. Determinant of Inverse

   $\det(A^{-1}) = \frac{1}{\det(A)}$

   This holds only if $\det(A) \neq 0$.

Relation Between Adjoint and Inverse

The adjoint matrix plays a crucial role in finding the inverse of a matrix. For a square matrix $A$ of order $n$:

$A^{-1} = \frac{\text{Adj}(A)}{\det(A)}, \quad \det(A) \neq 0$

This relation connects adjoint, determinant, and inverse.

• If $\det(A) = 0$, the matrix has no inverse, even though $\text{Adj}(A)$ may exist.

• The adjoint ensures a direct formula for the inverse without performing row operations.

Solved Examples Based on Adjoint of Matrix

Example 1: Let $\mathrm{A}$ be a matrix of order $3 \times 3$ and $\operatorname{det}(\mathrm{A})=2$. Then $\operatorname{det}\left(\operatorname{det}(\mathrm{A}) \operatorname{adj}\left(5 \operatorname{adj}\left(\mathrm{A}^3\right)\right)\right) {\text { is equal to }}$ $\qquad$ [JEE Main 2022]

Solution:
$
\begin{aligned}
& \operatorname{det}\left(2 \operatorname{adj}\left(5 \operatorname{adj}\left(\mathrm{A}^3\right)\right)\right) \\
& =2^3\left|\operatorname{adj}\left(5 \operatorname{adj}\left(\mathrm{A}^3\right)\right)\right| \\
& =2^3\left|5 \operatorname{adj}\left(\mathrm{A}^3\right)\right|^2 \\
& =2^3\left(5^3\left|\operatorname{adj}\left(\mathrm{A}^3\right)\right|\right)^2 \\
& =2^3 5^6\left(\left|\mathrm{~A}^3\right|^2\right)^2=2^3 5^6|\mathrm{~A}|^{12}=2^3 5^6 2^{12} \\
& =2^{15} 5^6=2^9 10^6=512 \times 10^6
\end{aligned}
$

Hence, the required answer is $512 \times 10^6$

Example 2: $\mathrm{A}=\left[\begin{array}{cc} 5 a & -b \\ 3 & 2 \end{array}\right] and\,\, \mathbf{A} \operatorname{adj} \mathbf{A}=\mathbf{A} \mathbf{A}^{T}, then \,\,5a+b \,\,is \,\,equal\,\, to :$

Solution:

$A = \begin{bmatrix} 5a & -b \\ 3 & 2 \end{bmatrix}$

$\Rightarrow \operatorname{adj}(A) = \begin{bmatrix} 2 & b \\ -3 & 5a \end{bmatrix}$

Hence, $A \cdot \operatorname{adj}(A) = \begin{bmatrix} 5a & -b \\ 3 & 2 \end{bmatrix} \begin{bmatrix} 2 & b \\ -3 & 5a \end{bmatrix}$

$= \begin{bmatrix} 10a + 3b & 0 \\ 0 & 10a + 3b \end{bmatrix}$

And, $A A^{T} = \begin{bmatrix} 5a & -b \\ 3 & 2 \end{bmatrix} \begin{bmatrix} 5a & 3 \\ -b & 2 \end{bmatrix}$

$= \begin{bmatrix} 25a^{2} + b^{2} & 15a - 2b \\ 15a - 2b & 13 \end{bmatrix}$

Given that these two matrices are equal, so by comparing their elements:

$15a - 2b = 0$

$10a + 3b = 13$

$\therefore a = \tfrac{2}{5}, \quad b = 3$

(Also, for these values $25a^2 + b^2 = 13$, so the solution is consistent.)

$\therefore 5a + b = 2 + 3 = 5$

Example 3: Let $A$ be a matrix of order $3 \times 3$ and $\det(A)=2$. Then $\det(\det(A) \text{adj} (5\text{adj}(A^3)))$ is equal to _______.

Solution:

$\begin{aligned} & \operatorname{det}\left(2 \operatorname{adj}\left(5 \operatorname{adj}\left(\mathrm{~A}^3\right)\right)\right) \\ & =2^3\left|\operatorname{adj}\left(5 \operatorname{adj}\left(\mathrm{~A}^3\right)\right)\right| \\ & =2^3\left|5 \operatorname{adj}\left(\mathrm{~A}^3\right)\right|^2 \\ & =2^3\left(5^3\left|\operatorname{adj}\left(\mathrm{~A}^3\right)\right|\right)^2 \\ & =2^3 5^6\left(\left|\mathrm{~A}^3\right|^2\right)^2=2^3 5^6|\mathrm{~A}|^{12}=2^3 5^6 2^{12} \\ & =2^{15} 5^6=2^9 10^6=512 \times 10^6\end{aligned}$

Example 4: Let $\mathrm{A}=\left(\begin{array}{cc}2 & -1 \\ 0 & 2\end{array}\right)$. If $\mathrm{B}=\mathrm{I}-{ }^5 \mathrm{C}_1(\operatorname{adj} \mathrm{~A})+{ }^5 \mathrm{C}_2(\operatorname{adj} \mathrm{~A})^2-\ldots-{ }^5 \mathrm{C}_5(\operatorname{adj} \mathrm{~A})^5$ then the sum of all elements of the matrix $B$ is

Solution:

As $I$ and $A$ are commutative in multiplication ($IA = AI$), they follow all identities.

$\mathrm{B} = (I - \operatorname{adj} A)^5$

$= \left(\begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix} - \begin{bmatrix}2 & 1 \\ 0 & 2\end{bmatrix}\right)^5$

$= \begin{bmatrix}-1 & -1 \\ 0 & -1\end{bmatrix}^5 \quad \text{...(i)}$

Now let $\begin{bmatrix}-1 & -1 \\ 0 & -1\end{bmatrix} = P$.

$\therefore P^2 = \begin{bmatrix}-1 & -1 \\ 0 & -1\end{bmatrix} \begin{bmatrix}-1 & -1 \\ 0 & -1\end{bmatrix}$

$= \begin{bmatrix}1 & 2 \\ 0 & 1\end{bmatrix}$

$P^4 = \begin{bmatrix}1 & 2 \\ 0 & 1\end{bmatrix} \begin{bmatrix}1 & 2 \\ 0 & 1\end{bmatrix}$

$= \begin{bmatrix}1 & 4 \\ 0 & 1\end{bmatrix}$

$B = P^5 = P^4 \cdot P = \begin{bmatrix}1 & 4 \\ 0 & 1\end{bmatrix} \begin{bmatrix}-1 & -1 \\ 0 & -1\end{bmatrix}$

$= \begin{bmatrix}-1 & -5 \\ 0 & -1\end{bmatrix}$

Example 5: Let $\mathrm{A} \& \mathrm{~B}$ be two $3 \times 3$ matrices such that $\mathrm{AB}=\mathrm{I}$ and $|\mathrm{A}|=\frac{1}{8}$. Then $|\operatorname{adj}(\mathrm{B} \operatorname{adj}(2 \mathrm{~A}))|$ is equal to?

Solution:

$\begin{aligned}|\mathrm{AB}|=1 \Rightarrow|\mathrm{~A}||\mathrm{B}|=1 \Rightarrow|\mathrm{~B}|=8 \\ |\operatorname{adj}(\mathrm{~B} \operatorname{adj}(2 \mathrm{~A}))|=|\mathrm{B} \operatorname{adj}(2 \mathrm{~A})|^2 \\ =|\mathrm{B}|^2|\operatorname{adj}(2 \mathrm{~A})|^2 \\ =|\mathrm{B}|^2\left(|2 \mathrm{~A}|^2\right)^2=|\mathrm{B}|^2\left(\left(2^3|\mathrm{~A}|\right)^2\right)^2 \\ =8 \times 8 \times\left(8 \times \frac{1}{8}\right)^4 \\ =64\end{aligned}$

List of topics related to the Adjoint and Inverse of a matrix

The study of adjoint and inverse of a matrix covers several important subtopics that help in solving linear equations, matrix transformations, and higher-level algebra problems. Below is a structured list of the most relevant topics that build a strong foundation in understanding the relation between adjoint, determinant, and inverse matrices.

NCERT Resources

To master the concepts of matrices, adjoint, and inverse, NCERT provides reliable study material for Class 12. Below are the key NCERT notes, solutions, and exemplar problems for Chapter 3 – Matrices, which will help in building a clear understanding and strong problem-solving approach.

NCERT Class 12 Maths Notes for Chapter 3 - Matrices

NCERT Solutions for Class 12 Maths for Chapter 3 - Matrices

NCERT Exemplar Class 12 Maths Solutions for Chapter 3 - Matrices

Practice Questions based on Adjoint and Inverse of a matrix

Strengthen your understanding of the adjoint and inverse of a matrix with carefully designed practice questions and MCQs. These problems will help you apply formulas, test concepts, and improve accuracy in matrix-related calculations.

Adjoint And Inverse Of A Matrix Practice Question Mcq

You can practice questions on the related topics using the links shared below: