Minors And Cofactors

Determinant of matrices

The determinant of a matrix A is a number that is calculated from the matrix. For a determinant to exist, matrix A must be a square matrix. The determinant of a matrix is denoted by det A or |A|. So, The determinant is a scalar value that is a certain function of the entries of a square matrix

For $2 \times 2$ matrices

$
\mathrm{A}=\left[\begin{array}{ll}
a_1 & a_2 \\
b_1 & b_2
\end{array}\right]
$

then $\operatorname{det} \mathrm{A}$ is :

$
|\mathrm{A}|=\left|\begin{array}{ll}
a_1 & a_2 \\
b_1 & b_2
\end{array}\right|=\mathrm{a}_1 \times \mathrm{b}_2-\mathrm{a}_2 \times \mathrm{b}_1
$

For a $3 \times 3$ matrix determinant can be calculated in the following way :
let $\mathrm{A}=\left[\begin{array}{lll}a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \\ c_1 & c_2 & c_3\end{array}\right]$
then we find $\operatorname{det} \mathrm{A}$ in following way

$
|A|=a_1\left(b_2 \cdot c_3-b_3 \cdot c_2\right)-a_2\left(b_1 \cdot c_3-c_1 b_3\right)+a_3\left(b_1 c_2-b_2 c_1\right)
$

This same process we follow to evaluate the determinant of the matrix of any order. Notice that we start the first term with the +ve sign then the 2nd with the -ve sign and the 3rd again with the +ve sign, this sign sequence is followed for any order of matrix.

This whole process is row-dependent, the same process can be done using columns, which means we can select elements along the column and delete their row and column compute the determinant of the out matrix, and then multiply it with the element that we select. And we will get the same result as we get while doing the whole process along the row.

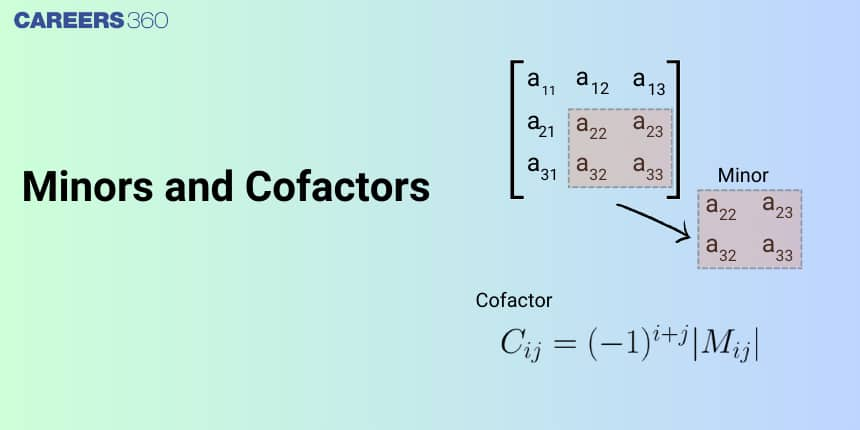
Minors of matrix

Minor is the value from the computation of a determinant of a square matrix, obtained by eliminating the row and the column that corresponds to the element under consideration.

Let A be a square matrix of order $\mathrm{n}(\mathrm{n} \geq 2)$ then the Minor of any element $a_{i j}$ where $\mathrm{i}, \mathrm{j}=1,2,3 \ldots . \mathrm{n}$ is the determinant of the matrix leftover after deleting the $\mathrm{i}^{\text {th }}$ row and $\mathrm{j}^{\text {th }}$ column, is called the minor of the element $a_{i j}$ and it is denoted by $\mathrm{M}_{\mathrm{ij}}$.

If we have the row and column passing through the element $a_{i j}$ then the second-order determinant formed by the remaining elements is called the minor of $a_{i j}$ and it is denoted by $M_{i j}$.

$
\mathrm{M}_{11}=\left|\begin{array}{ll}
a_{22} & a_{23} \\
a_{32} & a_{33}
\end{array}\right|=\mathrm{a}_{22} \mathrm{a}_{33}-\mathrm{a}_{23} \mathrm{a}_{32}
$

which is also the minor of determinant $A$ if we write $A$ in determinant form.
We can expand determinant w.r.t. any row or column. In each case, the value of the determinant is the same.

Cofactor of matrix

The cofactor of the matrix or determinant is the same as the minor of the matrix or determinant but the only difference is of sign, if $\mathrm{i}+\mathrm{j}$ is even then cofactor $=$ minor, if $\mathrm{i}+\mathrm{j}$ is odd then cofactor $=-$ minor,

$
\mathrm{C}_{\mathrm{ij}}=(-1)^{i+j} \mathrm{M}_{i j}
$

Or we can write, $\quad=\left\{\begin{array}{cc}M_{i j} & \text { if } \mathrm{i}+\mathrm{j} \text { is an even integer } \\ -M_{i j} & \text { if } \mathrm{i}+\mathrm{j} \text { is an odd integer }\end{array}\right.$

$
\mathrm{C}_{\mathrm{ij}} \text { is co - factor of } \mathrm{a}_{\mathrm{ij}}
$

For example,

$
\Delta=\left|\begin{array}{lll}
a_{11} & a_{12} & a_{13} \\
a_{21} & a_{22} & a_{23} \\
a_{31} & a_{32} & a_{33}
\end{array}\right|
$

then, minor of the element $\mathrm{a}_{21}$ is $M_{21}=\left|\begin{array}{ll}a_{12} & a_{13} \\ a_{32} & a_{33}\end{array}\right|$ and that of $\mathrm{a}_{32}$ is $M_{32}=\left|\begin{array}{ll}a_{11} & a_{13} \\ a_{21} & a_{23}\end{array}\right|$.
Cofactor of the element $a_{21}$ is

$
C_{21}=(-1)^{2+1} M_{21}=-\left|\begin{array}{ll}
a_{12} & a_{13} \\
a_{32} & a_{33}
\end{array}\right|
$

If we expand the determinant $\Delta$ along the first row, then the value of $\Delta$ in terms of minors is $\mathrm{a}_{11} \mathrm{M}_{11}$ $\mathrm{a}_{12} \mathrm{M}_{12}-\mathrm{a}_{13} \mathrm{M}_{13}$.

If we expand the determinant $\Delta$ along the first row, then the value of $\Delta$ in terms of co-factors is $\mathrm{a}_{11} \mathrm{C}_{11}+\mathrm{a}_{12} \mathrm{C}_{12}-\mathrm{a}_{13} \mathrm{C}_{13}$.

Thus, the products of the elements of any row or column with the corresponding cofactors are equal to the value of the determinant.

Also, the sum of the products of the elements of any row or column with the cofactors of the corresponding elements of any other row or column is zero.

Important Points

1) If any two rows (or columns) of a determinant are identical (all corresponding elements are the same), then the value of the determinant is zero.

2) If all the elements in one row or column are zero then the value of determinant is zero.

3) For easier calculations, we expand the determinant along that row or column which contains the maximum number of zeros.

Recommended Video Based on Minors and Cofactors

Solved Examples Based on Minors and Cofactors

Example 1: What is the minor of $\mathrm{a}_{23}$ in $\left|\begin{array}{ccc}1 & 3 & 5 \\ 8 & 2 & 1 \\ 5 & 6 & 10\end{array}\right|$ ?

Solution
Minor $M_{23}$ of the element $a_{23}$ is the determinant excluding the 2 nd row and 3rd column
So, minor $=\left|\begin{array}{ll}1 & 3 \\ 5 & 6\end{array}\right|=6-15=-9$
Hence, the answer is -9

Example 2: What is the co-factor of $\mathrm{a}_{33}$ in $\left|\begin{array}{lll}1 & 3 & 2 \\ 5 & 8 & 2 \\ 1 & 5 & 6\end{array}\right|$ ?

Solution
Minor of $a_{13}=\left|\begin{array}{ll}1 & 3 \\ 5 & 8\end{array}\right|=-7$
Cofactor of $\mathrm{a}_{13}=(-1)^{i+j} M_{i j}=(-1)^{1+3} M_{13}=-7$
Hence, the answer is -7