Polar Form of Complex Number - Meaning, Formula and Examples

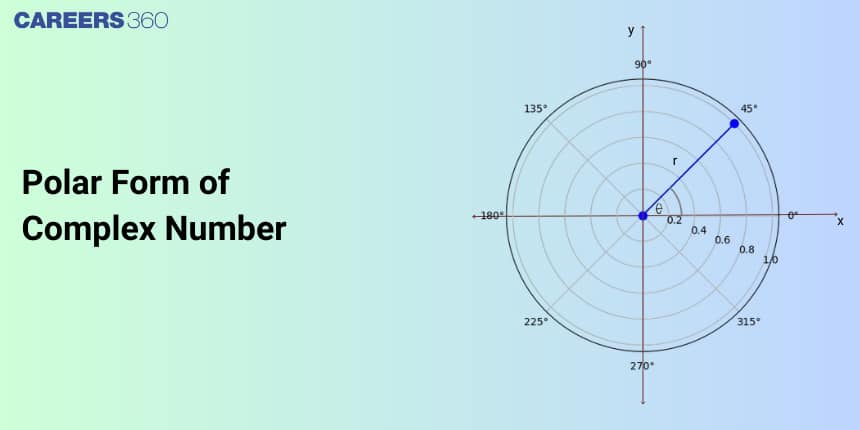
What is the Polar Form of Complex Numbers?

In polar form, we represent the complex number through the argument of complex number and modulus value of complex numbers.

Let $z=x+i y$ be a complex number,

And we know that

$|z|=\sqrt{x^2+y^2}=r$

And let arg(z) = θ

• The horizontal and vertical axes are the real axis and the imaginary axis, respectively.
• $r$ - the length of the vector and $\theta$ - the angle made with the real axis, are the real and complex components of the polar form of the complex number.
• There is a point P with coordinates $(x, y)$.
• The distance from the origin $(0,0)$ to point $P$ is given as $r$.
• The line joining the origin to point P makes an angle $\theta$ with the positive $x$ -axis.
• The polar coordinates are given as $(r, \theta)$ and rectangular coordinates are given as $(x, y)$.

Equation of Polar Form of Complex Numbers

The polar form of complex numbers is a fundamental concept in mathematics that connects algebra with geometry. It expresses a complex number in terms of its modulus and argument, making trigonometric applications and problem-solving easier.

Standard Polar Form Equation

From the figure, we know:

$x = |z| \cos \theta = r \cos \theta$
$y = |z| \sin \theta = r \sin \theta$

So, $z = x + i y = r(\cos \theta + i \sin \theta)$

This is called the polar form of a complex number, where $r = |z|$ is the modulus and $\theta$ is the argument.

• The principal value of the argument lies between $(-\pi, \pi]$.

• General form can be written as $z = r[\cos(2n\pi + \theta) + i \sin(2n\pi + \theta)], n \in \mathbb{Z}$.

Conversion from Rectangular Form to Polar Form of Complex Number

Rectangular form $z = a + bi$ can be converted into polar form using modulus and argument formulas.

Conversion Formula

$r = \sqrt{a^2 + b^2}, \quad \theta = \tan^{-1}(b/a)$

For example, consider $z = -2 + 2\sqrt{3}i$.

• $|z| = \sqrt{(-2)^2 + (2\sqrt{3})^2} = 4$

• $\theta = \tan^{-1}(-\sqrt{3})$, but since $z$ lies in the second quadrant, $\theta = 120^\circ$

So, $z = 4(\cos 120^\circ + i \sin 120^\circ)$.

Operations of Complex Numbers in Polar Form

The operations of complex numbers in polar form make addition and multiplication much easier to handle compared to rectangular form. Below, we explore the key formulas and methods for these operations.

Adding Complex numbers in Polar Form

Let $3 + 5i$ and $7 \angle 50^\circ$ be the two complex numbers. First, convert $7 \angle 50^\circ$ into rectangular form.

$x + iy = 7 \angle 50^\circ$

$x = 7 \cos 50^\circ = 4.5$
$y = 7 \sin 50^\circ = 5.36$

So, $7 \angle 50^\circ = 4.5 + i 5.36$

Adding the two complex numbers:
$(3 + 5i) + (4.5 + 5.36i) = 7.5 + i 10.36$

The modulus of the resulting complex number is: $r = |z| = \sqrt{x^2 + y^2}$
$r = \sqrt{7.5^2 + 10.36^2}$
$r = 12.79$

The argument of the resulting complex number is:
$\theta = \tan^{-1}(y/x)$
$\theta = \tan^{-1}(10.36 / 7.5)$
$\theta = 54.1^\circ$

Therefore, the required complex number in polar form is:
$12.79 \angle 54.1^\circ$

Product of Polar Form of Complex Number

Let $z = r_1 (\cos \theta_1 + i \sin \theta_1)$ and $w = r_2 (\cos \theta_2 + i \sin \theta_2)$ be two complex numbers in polar form.

The product of $z$ and $w$ is: $zw = r_1 (\cos \theta_1 + i \sin \theta_1) \times r_2 (\cos \theta_2 + i \sin \theta_2)$

Expanding the product:
$zw = r_1 r_2 [(\cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2) + i (\sin \theta_1 \cos \theta_2 + \cos \theta_1 \sin \theta_2)]$

Using the trigonometric addition formulas:
$zw = r_1 r_2 [\cos (\theta_1 + \theta_2) + i \sin (\theta_1 + \theta_2)]$

Important points

• The values of polar and rectangular coordinates are interdependent. Knowing any two values allows you to easily calculate the remaining values using the established relationships.

• The conversion formulas from rectangular to polar coordinates are:
  $r = \sqrt{x^2 + y^2}$
  $\theta = \tan^{-1} \frac{y}{x}$

• For any complex number $z = x + iy$, its modulus is given by:
  $|z| = \sqrt{x^2 + y^2}$

• The argument of $z$, denoted as $\operatorname{Arg}(z)$, is the angle formed by the line connecting $z$ to the origin with the positive real axis, and it lies in the interval $(-\pi, \pi)$.

Properties of Polar Form of Complex Numbers

The polar form of complex numbers provides an efficient way to perform multiplication, division, and find powers or roots of complex numbers. Using polar coordinates simplifies calculations and highlights the geometric interpretation in the Argand plane.

Multiplication in Polar Form

When multiplying two complex numbers in polar form, the moduli multiply and the arguments add.
Formula:
$z_1 z_2 = r_1 r_2 \big[\cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2)\big]$

This property is particularly useful for calculating the product of multiple complex numbers without converting them back to rectangular form.

Division in Polar Form

For division, the modulus of the numerator is divided by the modulus of the denominator, and the argument of the denominator is subtracted from the argument of the numerator.
Formula:
$\dfrac{z_1}{z_2} = \dfrac{r_1}{r_2} \big[\cos(\theta_1 - \theta_2) + i \sin(\theta_1 - \theta_2)\big]$

This method simplifies the process of finding quotients and is especially useful in signal processing and phasor analysis.

Powers of Complex Numbers (De Moivre’s Theorem)

De Moivre’s theorem provides a direct way to compute powers of complex numbers in polar form.
Formula:
$(\cos \theta + i \sin \theta)^n = \cos(n \theta) + i \sin(n \theta)$

This property helps in calculating higher powers without expanding multiple terms in rectangular form.

Roots of Complex Numbers in Polar Form

Finding $n^{th}$ roots of a complex number is straightforward using De Moivre’s theorem. The modulus is taken as the $n^{th}$ root, and the arguments are divided equally among $n$ roots.
Formula:
$z_k = r^{1/n} \left[\cos\left(\frac{\theta + 2k\pi}{n}\right) + i \sin\left(\frac{\theta + 2k\pi}{n}\right)\right], \quad k = 0, 1, 2, \dots, n-1$

This property is essential in solving polynomial equations and understanding symmetry in the Argand plane.

Solved Examples Based on Polar Form of a Complex Number

Example 1: If z is a non-real complex number, then the minimum value of $\frac{\operatorname{Im} z^5}{(\operatorname{Im} z)^3}$.

Solution:

As we have learned

Polar Form of a Complex Number -

$z=r(\cos \theta+i \sin \theta)$

- wherein

$\mathrm{z}=$ modulus of z and $\theta$ is the argument of Z

Euler's Form of a Complex Number -

$z=r e^{i \theta}$

- wherein

r denotes the modulus of z and $\theta$ denotes the argument of z.

$z=x+i y=r(\cos \theta+i \sin \theta)$

$=r e^{i \theta}$

So, $\operatorname{Im} z^5=\operatorname{Im}\left(r e^{i \theta}\right)^5$

$=\operatorname{Im}\left(r^5 e^{i \theta 5}\right)$

$=r^5 \sin 50$

$(\operatorname{Im} z)^5=(r \sin \theta)^5$

$=\left(r^5 \sin ^5 \theta\right)$

So, $\frac{\operatorname{Im} z^5}{(\operatorname{Im} z)^5}=\frac{\sin 5 \theta}{\sin ^5 \theta}$

for minimum value, differentiating w.r.t $\theta$

So, $\frac{\sin ^5 \theta \cdot 5 \cos \theta-5 \sin 5 \theta \sin ^4 \theta \cos \theta}{\sin ^{10} \theta}$

$\Rightarrow \sin \theta \cdot \cos 5 \theta-\sin 5 \theta \cos \theta=0$

$
\begin{aligned}
& \Rightarrow \sin 4 \theta \cdot=0 \\
& 4 \theta=n \pi \\
& \theta=n \pi / 4
\end{aligned}
$

for $\mathrm{n}=1$

$\frac{\sin 5 \theta}{\sin ^5 \theta}=\frac{-1 / \sqrt{2}}{(1 / \sqrt{2})^5}=-4$

Hence, the answer is -4.

Example 2: If z is a complex number of unit modulus and argument $\theta$ ,then arg $\left(\frac{1+z}{1+\bar{z}}\right)$ equals:

Solution:

$|z|=1$

$\operatorname{Arg}(z)=\theta$

So, $\frac{1+z}{1+\bar{z}}=\frac{1+\cos \theta+i \sin \theta}{1+\cos \theta-i \sin \theta}$

$\frac{2 \cos ^2 \theta / 2+2 i \sin \theta / 2 \cos \theta / 2}{2 \cos ^2 \theta / 2-2 i \sin \theta / 2 \cos \theta / 2}$

$=\frac{\cos \theta / 2+i \sin \theta / 2}{\cos \theta / 2-i \sin \theta / 2}$

$=\frac{e^{i \theta / 2}}{e^{-i \theta / 2}}$

$=e^{i \theta}$

Thus, arg$\left(\frac{1+z}{1+\bar{z}}\right)=\theta$

Hence, the answer is $\theta$.

Example 3: Let $z_1$ and $z_2$ be any two non-zero complex numbers such that $3\left|z_1\right|=2\left|z_2\right|$. If $z=\frac{3 z_1}{2 z_2}+\frac{2 z_2}{3 z_1}$ then :

1) $\operatorname{Re}(\mathrm{z})=0$
2) $=1=\sqrt{5 / 2}$
3) $|z|=\frac{1}{2} \sqrt{34}$
4) $\ln (z)=0$

Solution:

If $z=\frac{3 z 1}{222}+\frac{2 \pi 2}{32}$
Given, ${ }^3\left|Z_1\right|=2 \mid Z_2$
$\Rightarrow \frac{\left|3 Z_1\right|}{\left|2 Z_2\right|}=\left|\frac{3 Z_1}{2 Z_2}\right|=1$
$\operatorname{Let} \frac{3-1}{2 z 2}=a=\cos \theta+i \sin \theta$

$\begin{aligned} & z=a+\frac{1}{a} \\ & z=\cos \theta+i \sin \theta+\frac{1}{\cos \theta+i \sin \theta} \\ & z=\cos \theta+i \sin \theta+\frac{1}{\cos \theta+i \sin \theta} \times \frac{\cos \theta-i \sin \theta}{\cos \theta-i \sin \theta} \\ & z=\cos \theta+i \sin \theta+\frac{\cos \theta-i \sin \theta}{\cos ^2 \theta-i^2 \sin ^2 \theta} \quad\left(i^2=-1\right)\end{aligned}$

$\begin{aligned} & z=\cos \theta+i \sin \theta+\frac{\cos \theta-i \sin \theta}{1} \\ & z=2 \cos \theta+0 i \\ & \operatorname{Im}(z)=0 \end{aligned}$

Hence, the answer is the option 4.

Example 4: If $z$ and $w$ are two complex numbers such that $|z w|=1$ and $\arg (z)-\arg (w)=\frac{\pi}{2}$ then :

1) $z \bar{w}=i$

2) $z \bar{w}=\frac{-1+i}{\sqrt{2}}$

3) $\bar{z} w=-i$

4) $z \bar{w}=\frac{1-i}{\sqrt{2}}$

Solution:

Euler's Form of a Complex Number -

$z=r e^{i g}$

- wherein

r denotes the modulus of z and $\theta$ denotes the argument of z.

Polar Form of a Complex Number -

$z=r(\cos \theta+i \sin \theta)$

- wherein

r= modulus of z and $\theta$ is the argument of z

Now,

$|z w|=1_{\text {and }} \arg (z)-\arg (w)=\frac{\pi}{2}$

Let $|z|=r$ $=> z=r e^{i \theta}$

$|\omega|=\frac{1}{r}$ $=>\omega=\frac{1}{r} e^{i \phi}$

$\arg (z)-\arg (w)=\frac{\pi}{2}$

$\theta-\phi=\frac{\pi}{2}$

$\theta=\frac{\pi}{2}+\phi$

$z \bar{\omega}=r e^{i \theta} \cdot \frac{1}{r} e^{-i \phi}$

$=r e^{i(\theta-\phi)}$

$=r e^{i\left(\frac{\pi}{2}+\phi-\phi\right)}$

$\equiv r e^{i\left(\frac{\pi}{2}\right)}$

$=\cos \left(\frac{\pi}{2}\right)+i \sin \left(\frac{\pi}{2}\right)$

$=0+i .1$

$=i$

Hence, the answer is the option (1).

Example 5: Polar form of $z=\frac{1+7 i}{(2-i)^2}$ will be :

Solution:

As we learned in

Polar Form of a Complex Number

$z=r(\cos \theta+i \sin \theta)$

where r is the modulus of z and $\theta$ is the argument of z

Now,

$z=\frac{1+7 i}{(2-i)^2}=\frac{1+7 i}{3-4 i} \times \frac{3+4 i}{3+4 i}=\frac{-25+25 i}{25}$

$\Rightarrow z=-1+i$

$r=|z|=\sqrt{2}$ and $\arg (z)=\pi-\tan ^{-1} \frac{1}{-1}$

$\begin{aligned} & \Rightarrow r=\sqrt{2} \text { and } \arg (z)=\pi-\frac{\pi}{4}=\frac{3 \pi}{4} \\ & \therefore z=\sqrt{2}\left(\cos \frac{3 \pi}{4}+i \sin \frac{3 \pi}{4}\right)\end{aligned}$

Hence, the answer is $\sqrt{2}\left(\cos \frac{3 \pi}{4}+i \sin \frac{3 \pi}{4}\right)$.

List of topics related to the Polar form of a Complex Numbers

Below is a list of important topics connected to the polar form of complex numbers, which will help you in learning formulas, properties, and applications in a structured way.

NCERT Resources

Below you can access NCERT Solutions, Exemplar problems, and concise notes for Class 11 Maths Chapter 5 – Complex Numbers and Quadratic Equations. These resources will help in understanding concepts and practicing exam-relevant questions.

NCERT Solutions for Class 11 Maths Chapter 5 -Complex Numbers and Quadratic Equations

NCERT Exemplar Class 11 Maths Solutions for Chapter 5 - Complex Numbers and Quadratic Equations

NCERT Class 11 Maths Notes for Chapter 5 - Complex Numbers and Quadratic Equations

Practice Questions based on the Polar form of a Complex Number

Below are some practice questions designed to help you strengthen your understanding of the polar form of complex numbers.

Polar Form Of Complex Numbers - Practice Question MCQ

We have shared practice questions sets for related topics below: