Irrational equations and Inequalities: Problems with Solutions
Mastering irrational equations and inequalities is crucial for both Class 11 Maths and competitive exams like JEE. These problems often involve square roots and require careful domain analysis and algebraic manipulation. This topic includes a wide range of irrational equations and inequalities questions, helping students gain confidence in solving complex expressions. Whether you're tackling the irrational inequalities Class 11 syllabus or preparing for irrational inequalities JEE level challenges, this article offers structured explanations and solved problems to support your learning. In this article, you'll learn the key concepts, methods, and examples to solve irrational inequalities and equations effectively.
- What are Irrational Equations?
- What are Irrational Inequalities?
- NCERT Resources
- Practice Questions Based on Irrational Equations and Inequalities
- List of Topics Related to Irrational Equations and Inequalities
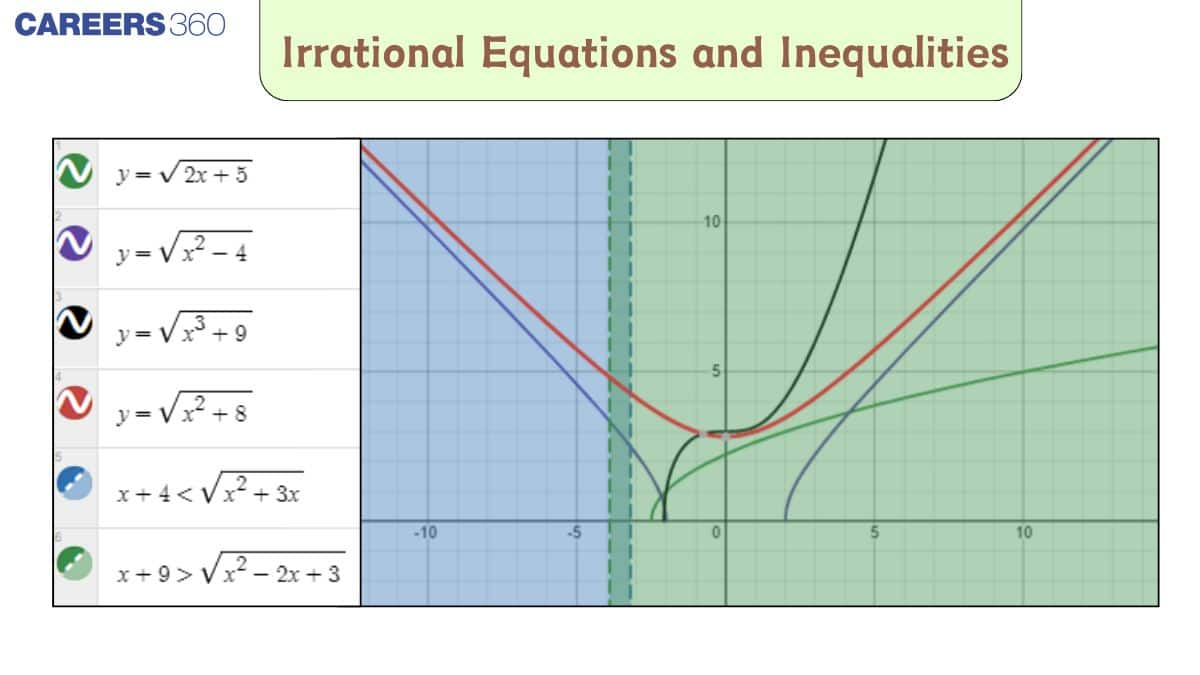
What are Irrational Equations?
Understand the basics of irrational equations, involving roots or surds in variables. This section covers key forms, solution steps, and conditions for solving irrational inequalities and equations effectively.
Definition of Irrational Equations
An irrational equation is an algebraic equation that contains one or more irrational expressions, usually involving square roots, cube roots, or higher-order roots of algebraic expressions. These equations often require careful manipulation to isolate and eliminate the irrational part.
For example, an equation like
$\sqrt{x + 2} = x - 1$
is an irrational equation because the variable $x$ is under a square root.
Common Forms and Examples
Some common forms of irrational equations include:
$\sqrt{f(x)} = g(x)$
$\sqrt{f(x)} + \sqrt{g(x)} = h(x)$
$\frac{1}{\sqrt{x}} = x + 1$
Examples:
$\sqrt{2x + 3} = x - 1$
$\sqrt{x + 4} + \sqrt{3x - 1} = 5$
$\frac{1}{\sqrt{x - 2}} = x$
These forms frequently form the base for irrational inequality questions as well, when an inequality sign is involved.
Conditions for Existence of Solutions
Before solving irrational equations, it is important to identify the domain of validity. Since square roots (and other even-order roots) are defined only for non-negative values, we must ensure:
The expression inside a square root must be non-negative, i.e.,
If $\sqrt{f(x)}$ appears, then solve $f(x) \geq 0$If the irrational term appears in a denominator, then the expression inside the root must be strictly positive, i.e.,
If $\frac{1}{\sqrt{f(x)}}$ appears, then solve $f(x) > 0$
These domain restrictions play a crucial role while solving irrational inequalities and must not be ignored.
Steps to Solve Irrational Equations
Here’s a general step-by-step strategy to solve an irrational equation:
Isolate the Irrational Expression:
Try to bring the root term (like $\sqrt{f(x)}$) to one side of the equation.Square Both Sides:
Remove the square root by squaring both sides. For example,
$\sqrt{x + 2} = x - 1 \Rightarrow x + 2 = (x - 1)^2$Simplify and Solve the Resulting Polynomial Equation:
After removing the root, simplify the expression and solve for $x$.Check for Extraneous Solutions:
Squaring may introduce invalid solutions. Substitute your answers back into the original equation to verify their validity.
What are Irrational Inequalities?
Understand the basics of irrational equations, involving roots or surds in variables. This section covers key forms, solution steps, and conditions for solving irrational inequalities and equations effectively.
Definition of Irrational Inequalities
An irrational inequality is an inequality that includes at least one irrational expression, usually involving roots like square roots or cube roots of algebraic functions. These types of inequalities require careful handling due to the presence of non-linear terms.
For example:
$\sqrt{x - 1} > 3$
$\frac{1}{\sqrt{x + 2}} < 4$
$\sqrt{2x + 3} \leq x - 1$
Such inequalities are frequently tested in irrational inequalities Class 11 and also form an integral part of irrational inequalities JEE syllabus.
Forms of Inequalities:
Common forms of irrational inequalities include:
$\sqrt{f(x)} > g(x)$
$\sqrt{f(x)} < g(x)$
$\frac{1}{\sqrt{f(x)}} \geq g(x)$
$\sqrt{f(x)} + \sqrt{g(x)} < h(x)$
Each type requires a specific approach that involves squaring, domain analysis, and sign analysis.
Inequalities are the relationship between two expressions that are not equal to one another. Symbols denoting the inequalities are <, >, ≤, ≥, and ≠.
- $x<4$, "is read as $x$ less than $4^{\prime \prime}, x \leq 4$, is read as $x$ less than or equal to $4^{\prime \prime}$.
- Similarly $x>4$, "is read as $x$ greater than $4^{\circ}$ and $x \geq 4$, "is read as $x$ greater than or equal to 4 ".
The process of solving inequalities is the same as of equality but instead of equality symbol inequality symbol is used throughout the process.
Types of Inequalities
- Linear Inequalities: Involve linear expressions.
- Example: $2 x+3 \leq 7$
- Quadratic Inequalities: Involve quadratic expressions.
- Example: $x^2-4 x+3 \geq 0$
- Polynomial Inequalities: Involve polynomials of degree greater than two.
- Example: $x^3-2 x^2+x-5<0$
- Rational Inequalities: Involve ratios of polynomials.
- Example: $\frac{x+1}{x-3} \geq 2$
- Absolute Value Inequalities: Involve absolute value expressions.
- Example: $|x-2| \leq 5$
Key Concepts to Consider
Before solving irrational inequalities, it’s important to remember the following:
Domain Restrictions:
If the inequality involves $\sqrt{f(x)}$, then the domain is given by $f(x) \geq 0$.Squaring Caution:
Squaring both sides of an inequality can change the nature of the inequality if signs are not properly accounted for. It is valid only when both sides are non-negative.Critical Points and Intervals:
After simplification, always break the solution into intervals using critical points. Test each interval in the original inequality.Reject Extraneous Solutions:
As with irrational equations, squaring may introduce false roots. Always verify with the original inequality.
Example Problems
Solve: $\sqrt{x + 1} \leq x$
Step 1: Domain
$x + 1 \geq 0 \Rightarrow x \geq -1$
Step 2: Square both sides
$\sqrt{x + 1} \leq x \Rightarrow x + 1 \leq x^2$
Step 3: Rearrange
$x^2 - x - 1 \geq 0$
Step 4: Solve the quadratic inequality
The roots of $x^2 - x - 1 = 0$ are $x = \frac{1 \pm \sqrt{5}}{2}$
Step 5: Find intervals satisfying the inequality
Use sign analysis to find that $x \leq \frac{1 - \sqrt{5}}{2}$ or $x \geq \frac{1 + \sqrt{5}}{2}$
But from domain, $x \geq -1$
Final Answer:
$x \in \left[\frac{1 + \sqrt{5}}{2}, \infty\right)$
Graphical Interpretation
For e.g. a $>3$ gives us a range of solutions, means $(3, \infty)$
Graphically inequalities can be shown as a region belonging to one side of the line or between lines, for example, inequality $-3<x \leq 5$ can be represented as below, a region belonging to $-3$ and $5$ are the region of possible $x$ including $45$ and excluding $-3$ .

Irrational inequalities are inequalities with irrational equations. For example, $\sqrt{x^2+7} = 4$
If $n$ is odd
To solve inequations of the form $(f(x))^{1 / n}>g(x)$ or $(f(x))^{1 / n}<g(x)$, or $(f(x))^{1 / n}>(g(x))^{1 / n}$, raise both sides to the power $n$, and solve to get the answer.
If $n$ is even
1. To solve inequations of the form $(f(x))^{1 / n}>g(x)$,
a. LHS should be defined, so solve $f(x) \geq 0$
b. Now if $\mathrm{g}(\mathrm{x})<0$, then LHS will be greater than RHS for all such values
c. If $g(x) \geq 0$, then solve $f(x)>(g(x))^n$
In the end take the intersection of a with (b union c)
2. To solve inequations of the form $(f(x))^{1 / n}<g(x)$,
a. LHS should be defined, so solve $f(x) \geq 0$
b. Now if $\mathrm{g}(\mathrm{x})<0$, then LHS will be not be lesser than RHS for all such values
c. If $g(x) \geq 0$, then solve $f(x)<(g(x))^n$
In the end take intersection of $a$ and $c$.
Solved Examples Based On Irrational Inequalities and Equations:
Example 1: Solve the inequality $\sqrt{x+14}<x+2$
Solution:
$\sqrt{x+14}<x+2$
1. For LHS to be defined, $x+14 \geq 0$ means $x \geq-14$
2. When $x+2 \leqslant 0$, then RHS cannot be greater than LHS, so no answer from this case
3. When $x+2 \geq 0$, means when $x \geq-2$,
In this case, we can square both sides
$
\begin{aligned}
& x+14<(x+2)^2 \\
& x+14<x^2+4 x+4 \\
& x^2+3 x-10>0 \\
& (x+5)(x-2)>0 \\
& x<-5 \text { or } x>2
\end{aligned}
$
Taking intersection with $x \geq-2$, which equals $x>2$
Now, the answer is the intersection of (1) and (3), which is $x>2$
Example 2: Which of the options is correct for the inequality $\sqrt{-x^2+4 x-3}>6-2 x ?$
1) $(1,3)$
2) $\left(\frac{13}{5}, 3\right)$
3) $(3, \infty)$
4) $(-\infty, 3)$
Solution
1. LHS should be defined, so
$-x^2+4 x-3 \geq 0$
$\begin{aligned} & x^2-4 x+3 \leq 0 \\ & (x-1)(x-3) \leq 0 \\ & 1 \leq x \leq 3\end{aligned}$
2. When RHS < 0, then all these values will satisfy the inequation
$6-2 x<0$
$\Rightarrow x>2$
3. When RHS 0 (when $x \leq 3$ ), then we can square the inequation
$
\begin{aligned}
& -x^2+4 x-3>(6-2 x)^2 \\
& -x^2+4 x-3>36+4 x^2-24 x \\
& 5 x^2-28 x+39<0 \\
& (x-3)(5 x-13)<0 \\
& 13 / 5<x<3
\end{aligned}
$
Taking the intersection of this result with $x<3$, we get the interval of x , i.e
$13 / 5<x<3$
Hence, the answer is the option 2.
Example 3: If x is a solution of the equation , $\sqrt{2 x+1}-\sqrt{2 x-1}=1,\left(x \geqslant \frac{1}{2}\right)$, then $\sqrt{4 x^2-1}$ is equal to :
Solution:
$
\begin{aligned}
& \sqrt{2 x+1}-\sqrt{2 x-1}=1 \\
& \Rightarrow \sqrt{2 x+1}=\sqrt{2 x-1}+1
\end{aligned}
$
square both side
$
\begin{aligned}
& \Rightarrow 2 x+1=2 x-1+1+2 \sqrt{2 x-1} \\
& \Rightarrow 1=2 \sqrt{2 x-1}
\end{aligned}
$
square both side
$
\begin{aligned}
& \Rightarrow 2 x-1=\frac{1}{4} \\
& \Rightarrow x=\frac{5}{8}
\end{aligned}
$
Now $\sqrt{4 x^2-1}$ at $x=5 / 8 \Rightarrow \sqrt{4 \times \frac{25}{64}-1}=3 / 4$
Example 4: Let $S={ }^{-1}$ R: $x>0$ 0 and $2|\sqrt{x}-3|+\sqrt{x}(\sqrt{x}-6)+6=0$ Then S:
1) contains exactly four elements
2) is an empty set.
3) contains exactly one element
4) contains exactly two elements
Solution:
Roots of Quadratic Equation -
$\alpha=\frac{-b+\sqrt{b^2-4 a c}}{2 a}$
$\beta=\frac{-b-\sqrt{b^2-4 a c}}{2 a}$
- wherein
$a x^2+b x+c=0$
is the equation
$a, b, c \in R, \quad a \neq 0$
Case 1
$\sqrt{x} \geq 3 \Rightarrow x \geq 9$
$2(t-3)+t(t-6)+6=0$
$t^2-4 t=0$
$\Rightarrow t=0, t=4$
$\sqrt{x}=0, \sqrt{x}=4$
$x=0, x=16$
we take $x=16$ $x \geq 9$
case 2
$0<\sqrt{x}<3 \Rightarrow 0<x<9$
$-2 t+6+t^2-6 t+6=0$
$t^2-8 t+12=0$
$\Rightarrow t=2, t=6$
$\Rightarrow x=4, x=36$
Thus $x=4$ : $x<9$
So there are two elements
Hence, the answer is the option 4.
Example 5: Solve $x-3 \sqrt{x+1}+3=0$
Solution:
$\begin{aligned} & x-3 \sqrt{x+1}+3=0 \\ & \text { Let } \sqrt{x+1}=t \\ & \Rightarrow x+1=t^2 \\ & \Rightarrow x=t^2-1\end{aligned}$
So, the equation becomes
$\begin{aligned} & \left(t^2-1\right)-3 t+3=0 \\ \Rightarrow & t^2-3 t+2=0 \\ \Rightarrow & (t-1)(t-2)=0 \\ \Rightarrow & t=1, t=2 \\ \Rightarrow & \sqrt{x+1}=1, \quad \sqrt{x+1}=2 \\ \Rightarrow & x+1=1, \quad x+1=4 \\ \Rightarrow & x=0, \quad x=3\end{aligned}$
NCERT Resources
Explore curated NCERT study materials for Class 11 Chapter 5 "Complex Numbers and Quadratic Equations" including detailed notes, solutions, and exemplar problems. These resources are essential for mastering the fundamentals and aligning with the CBSE curriculum.
Practice Questions Based on Irrational Equations and Inequalities
Sharpen your skills with irrational inequalities questions and irrational equation problems through concept-based MCQs. These practice sets are designed to strengthen your understanding of domain analysis, squaring techniques, and solution verification.
Irrational Equations and Inequalities Practice Question MCQ
Below are the next topics, which you can practice to gain more understanding:
List of Topics Related to Irrational Equations and Inequalities
Explore the most relevant topics connected to irrational equations and various classes of inequalities. Each link opens a Careers360 topic page with explanations, formulas, and solved examples.
Frequently Asked Questions (FAQs)
Inequalities are the relationship between two expressions that are not equal to one another.
An irrational equation is an equation where the variable is inside the radical or the variable is a base of power with fractional exponents.
$2^{\sqrt{\sin ^2 x-2 \sin x+5}} \cdot \frac{1}{4^{\sin ^2 y}} \leq 1$
$ 2^{\sqrt{\sin ^2 x-2 \sin x+5}<2^{2 \sin 2}}$
$\sqrt{\sin ^2 x-2 \sin x+5} \leq 2 \sin ^2 y$
$\sqrt{(\sin x-1)^2+4} \leq 2 \sin ^2 y$
$\Rightarrow \sin x=1 \&|\sin y|=1$
$-5(x-1) \leqslant 010(2 x-3)$
$\Rightarrow \quad(x-1) \geqslant \frac{10}{-5}(2 x-3)$
$\Rightarrow x-1 \geqslant-2(2 x-3)$
$\Rightarrow x-1 \geqslant-4 x+6$
$\Rightarrow x+4 x \geqslant 6+1$
$\Rightarrow 5 x \geqslant 7$
$\Rightarrow x \geqslant \frac{7}{5}$
$-\frac{1}{2}<x \leqslant 3\left(-\frac{1}{2}<0,3>0\right)$
$\Rightarrow-\frac{1}{2}<x<0^{-} \text {or } 0^{+}<x \leqslant 3$
$\Rightarrow-2>\frac{1}{x}>-\infty \text { or } \infty>\frac{1}{x} \geqslant \frac{1}{3}$
$\Rightarrow \frac{1}{x} \in(-\infty,-2) \cup\left[\frac{1}{3}, \infty\right)$
An irrational equation is an equation that contains at least one term with a variable under a square root (or other root) sign. These equations often require special techniques to solve, as the presence of the root can complicate the process.
Irrational inequalities are similar to irrational equations but use inequality symbols (<, >, ≤, ≥) instead of an equals sign. They require additional steps to solve, including considering the domain of the expression and potential extraneous solutions.
Checking solutions is crucial because the process of solving irrational equations often involves squaring both sides, which can introduce extraneous solutions. These are values that satisfy the squared equation but not the original equation.
The domain of an irrational equation is the set of all possible values for the variable that make the equation meaningful. It's important because it helps identify restrictions on the solution set and can prevent errors when solving the equation.
To solve an equation with a square root, typically you isolate the square root term on one side, then square both sides of the equation. This eliminates the square root, but remember to check for extraneous solutions afterward.
Rational equations contain variables in the numerator or denominator of fractions, while irrational equations contain variables under root signs. Irrational equations often require more complex solving techniques and careful consideration of domains.
Yes, an irrational equation can have no solution. This occurs when the domain restrictions of the irrational expression cannot be satisfied by any real number, or when squaring both sides leads to a contradiction.
Rationalizing refers to the process of eliminating irrational terms (like square roots) from an equation. This is often done by multiplying both sides of the equation by a carefully chosen expression that cancels out the irrational term.
To solve an irrational inequality: 1) Isolate the irrational term, 2) Square both sides if dealing with a square root, 3) Solve the resulting rational inequality, 4) Check the domain of the original inequality, and 5) Test points to determine the final solution set.
Squaring both sides can change the solution set because it's not a reversible operation. It can introduce extraneous solutions that satisfy the squared equation but not the original one. This is why checking solutions is crucial.
The discriminant (b²-4ac in a quadratic ax²+bx+c) helps determine the nature of the solutions to a quadratic equation. In irrational equations, it can indicate whether the equation has real solutions, which is crucial for determining the overall solution set.
For equations with multiple radical terms, isolate one radical term on one side of the equation. Then, square both sides to eliminate that radical. Repeat this process until all radicals are eliminated, being careful to check for extraneous solutions at each step.
Graphing can provide visual insight into the behavior of irrational equations and inequalities. It can help identify the number and approximate location of solutions, as well as illustrate the domain and range of the expressions involved.
Absolute value can appear in irrational equations, often in the form of square roots of squared terms. Understanding that √(x²) = |x| is crucial for solving these types of equations and interpreting their solutions correctly.
Some irrational equations may lead to complex number solutions, especially when the equation involves even-indexed roots of negative numbers. Understanding complex numbers is essential for fully characterizing the solution set of certain irrational equations.
To determine if an irrational equation has real solutions, consider the domain of the irrational expressions and any restrictions imposed by the equation. If the domain is empty or the restrictions cannot be satisfied by real numbers, the equation has no real solutions.
The term under the radical is crucial as it determines the domain of the equation. For square roots, this term must be non-negative for real solutions. Understanding this helps in solving the equation and interpreting its solutions.
For cube root equations, isolate the cube root term, then cube both sides of the equation. Unlike with square roots, cubing doesn't introduce extraneous solutions, but it's still important to check the domain of the original equation.
Common mistakes include: forgetting to check for extraneous solutions, ignoring domain restrictions, incorrectly applying algebraic operations to radicals, and failing to consider the possibility of complex solutions.
Graphically, the solution to an irrational inequality represents the x-values where the graph of one side of the inequality is above or below (depending on the inequality sign) the graph of the other side.
Irrational equations often involve roots, which are fractional exponents. Understanding the properties of exponents, especially fractional and negative exponents, is crucial for manipulating and solving irrational equations.
For such equations, try to isolate terms with the variable inside the radical on one side and terms with the variable outside on the other. Then square both sides. This may lead to a quadratic equation, which can be solved using standard methods.
Function composition is often implicitly used in solving irrational equations, especially when isolating radical terms. Understanding how composite functions work helps in correctly manipulating the equation and interpreting the results.
To solve an irrational inequality with absolute values, first solve the equation formed by replacing the inequality sign with an equals sign. Then, use the solutions as boundary points to test intervals and determine where the inequality holds true.
The zero-product property (if ab = 0, then a = 0 or b = 0) is often useful after squaring both sides of an irrational equation. It helps in breaking down the resulting equation into simpler parts that can be solved individually.
The number of solutions depends on the specific equation. Consider the degree of the equation after rationalizing, the nature of the irrational terms, and any domain restrictions. Graphing can also provide insight into the number of intersections or solutions.
This principle states that if two expressions are equal, their corresponding parts must also be equal. It's useful in solving complex irrational equations by allowing you to equate the rational and irrational parts separately.
If squaring leads to a higher-degree polynomial, standard techniques like factoring, using the quadratic formula (for degree 2), or polynomial solving methods (for higher degrees) may be necessary. Always check solutions in the original equation.
Interval notation is a concise way to express the solution set of irrational inequalities. It clearly shows the range of values that satisfy the inequality, including any restrictions or discontinuities in the solution set.
To solve a system of irrational equations, you can use substitution or elimination methods, but be careful to square terms appropriately. After solving, check solutions in both original equations to eliminate any extraneous solutions introduced by squaring.
Inverse functions are often used implicitly when solving irrational equations. For example, squaring both sides of an equation involving a square root is equivalent to applying the inverse function (squaring) to both sides.
For equations with multiple radicals, isolate one radical term and square both sides. Repeat this process until all radicals are eliminated. Be extra careful to check for extraneous solutions, as each squaring step can introduce them.
Understanding even and odd functions helps in predicting the behavior of solutions. For example, even-indexed roots of negative numbers may lead to complex solutions, while odd-indexed roots always have real solutions for real inputs.
For equations involving both radicals and logarithms, try to isolate the radical term first, then square both sides. This often results in an equation with logarithms, which can be solved using logarithm properties and exponential functions.
Completing the square can be useful in irrational equations, especially when squaring both sides results in a quadratic equation. It helps in simplifying the equation and can make it easier to identify the nature and number of solutions.
The strictness of an irrational inequality depends on the original inequality sign (< or > for strict, ≤ or ≥ for non-strict) and the nature of the irrational expression. Be careful when squaring, as it can affect the inequality direction for negative terms.
Parametric equations can be useful in solving complex irrational equations by introducing a parameter to simplify the equation. This approach can help in finding solutions that might be difficult to obtain through direct algebraic manipulation.
If solving an irrational equation leads to a rational equation with a zero denominator, it usually indicates that the original equation has no solution for that particular value. Always check the domain of the original equation to confirm this.
Continuity is crucial in solving irrational inequalities because it helps in identifying where the inequality might change direction. Points of discontinuity often occur at the boundaries of the domain and can be critical points in determining the solution set.
For nested radicals, start by isolating the outermost radical. Square both sides to remove it, then repeat the process for inner radicals. This often leads to a complex equation, so be extra vigilant about checking for extraneous solutions.
The intermediate value theorem helps in proving the existence of solutions to irrational equations. If a continuous function changes sign over an interval, this theorem guarantees that there's at least one solution within that interval.
For equations where the variable is both in the base and exponent, try to isolate terms with the variable in the exponent on one side. Then use logarithms to bring the variable down from the exponent. This often results in an equation that can be solved algebraically.
Asymptotes are important in irrational inequalities as they often represent boundaries of the solution set. Vertical asymptotes can indicate where the inequality changes direction, while horizontal asymptotes can help in understanding the behavior of the inequality for large values of the variable.
For equations with both radicals and trigonometric functions, try to isolate the radical term first. After squaring, you'll likely have an equation involving trigonometric functions, which can be solved using trigonometric identities and techniques.
The rational root theorem can be useful after rationalizing an irrational equation, especially if it results in a polynomial equation. It helps in identifying potential rational solutions, which can simplify the solving process.
For piecewise irrational inequalities, solve the inequality for each piece separately, paying attention to the domain of each piece. Then combine the results, being careful about the intervals where each piece is defined.
Monotonicity helps in determining how an irrational inequality behaves over different intervals. If a function is monotonic (always increasing or always decreasing) over an interval, it simplifies the process of determining where the inequality is satisfied.
For irrational equations with complex numbers, use similar techniques as with real numbers, but be prepared for complex solutions. Remember that even-indexed roots of negative numbers will yield complex results. Always express final answers in standard complex form (a + bi).
The squeeze theorem can be useful in solving complex irrational inequalities, especially when direct algebraic methods are difficult. It helps in determining the behavior of the inequality by comparing it to simpler functions that bound it from above and below.
For equations or inequalities without clear algebraic solutions, consider numerical methods or graphical approaches. Plotting the functions involved can provide insight into the number and approximate location of solutions. In some cases, computer algebra systems may be necessary for more precise results.
Also Read
04 Aug'25 07:39 PM
23 Jul'25 04:20 PM
02 Jul'25 08:09 PM
02 Jul'25 08:07 PM
02 Jul'25 08:06 PM
02 Jul'25 08:06 PM
02 Jul'25 08:03 PM
02 Jul'25 08:02 PM
02 Jul'25 08:02 PM
02 Jul'25 08:01 PM
