Complex Numbers and Quadratic Equations - Topics, Books, Preparation Tips FAQs
Complex numbers and quadratic equations are a key part of Class 11 Maths. This chapter helps you understand how to work with complex numbers, perform operations, and solve quadratic equations with real or imaginary roots. You will also learn important formulas, examples, and practice exercises that make solving problems easier in mathematics, whether for NCERT, JEE Main, or school exams. In this article, we cover everything you need to know about complex numbers and quadratic equations like formulae,nature of roots and other related topics, including notes, formulas, solutions, and practice questions.
This Story also Contains
- Complex Numbers: Definition
- Quadratic Equations: Definition
- Complex Numbers Formulae
- Quadratic Equations
- Solved examples based on Complex Numbers and Quadratic Equations
- List of Topics related to Complex Numbers according to NCERT/JEE MAIN
- NCERT Resources
- Practice Questions based on Complex Numbers and Quadratic Equations
Complex Numbers: Definition
A complex number is a number that can be expressed in the form $x + iy$, where $x$ and $y$ are real numbers and $i$ is the imaginary unit, also called iota. Complex numbers are used to represent quantities that cannot be expressed on the real number line alone.
Example:
$z = 5 + 2i$
Real part: $\operatorname{Re}(z) = 5$
Imaginary part: $\operatorname{Im}(z) = 2$
The imaginary unit $i$ (iota) is defined as:
$i = \sqrt{-1}$
Powers of $i$
The first few powers of $i$ are important for calculations:
$i^2 = -1$
$i^3 = -i$
$i^4 = 1$
Special Cases
Purely real number: If $\operatorname{Im}(z) = 0$, the complex number becomes a real number.
Example: $2 + 0i = 2$Purely imaginary number: If $\operatorname{Re}(z) = 0$, the complex number becomes purely imaginary.
Example: $0 + 2i = 2i$
Quadratic Equations: Definition
The highest power of the variable in a polynomial expression is called the degree of the polynomial.
A polynomial equation in which the highest degree of a variable term is $2$ is called a quadratic equation.
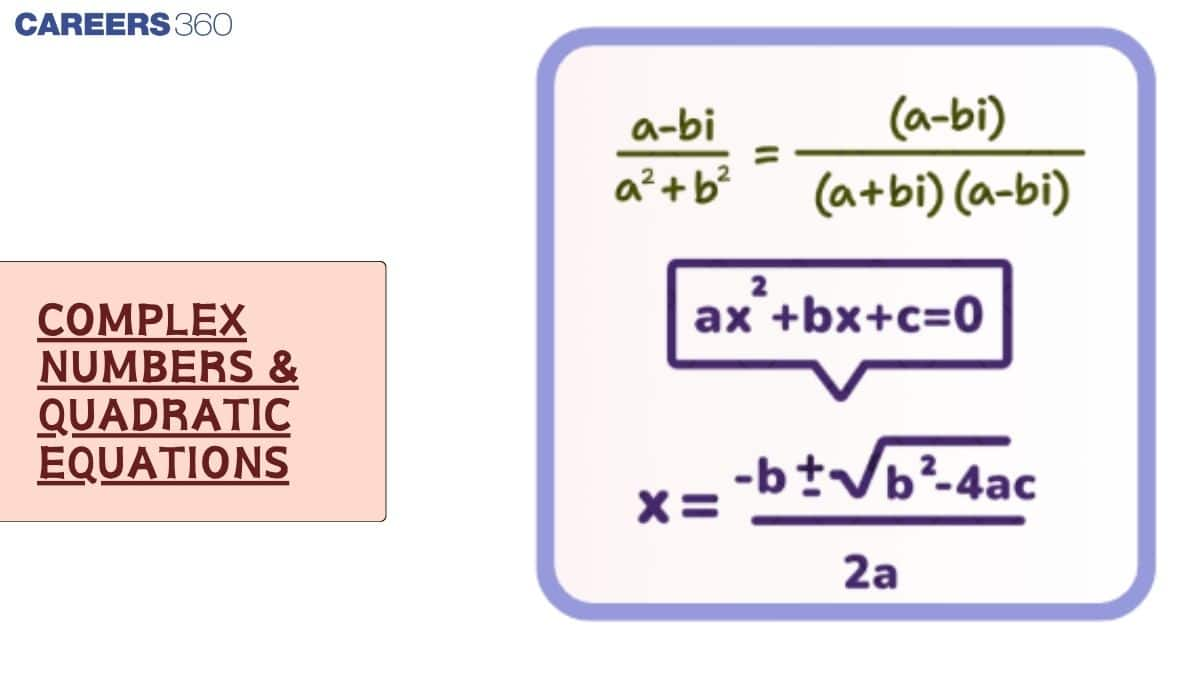
The standard form of a quadratic equation is: $a x^2 + b x + c = 0, \quad a \neq 0$
Here, $a$, $b$, and $c$ are constants (they may be real or complex) and are called the coefficients of the equation. $a$ is also called the leading coefficient.
Examples: $-5x^2 - 3x + 2 = 0$
$x^2 = 0$
$(1+i)x^2 - 3x + 2i = 0$
Since the degree of a quadratic polynomial is $2$, it always has 2 roots (number of real roots + number of imaginary roots = $2$).
Roots of Quadratic Equations
If $f(x)$ is a polynomial, then the equation $f(x) = 0$ is called a polynomial equation.
The roots of the polynomial equation are the values of $x$ for which $f(x) = 0$.
If $x = \alpha$ is a root of $f(x) = 0$, then:
$f(\alpha) = 0$
Example: For $x^2 - 3x + 2 = 0$, $x = 2$ is a root because: $f(2) = 2^2 - 3(2) + 2 = 4 - 6 + 2 = 0$
A polynomial of degree $n$ has $n$ roots (real or complex). Therefore, a quadratic equation always has exactly $2$ roots.
Complex Numbers Formulae
This section covers the essential formulae related to complex numbers, including conjugates, modulus, square roots, and algebraic operations. Understanding these formulae helps simplify calculations and solve problems involving complex numbers efficiently.
Conjugate of Complex Numbers
The conjugate of a complex number $z$ is represented by $\bar{z}$. The pair $(z, \bar{z})$ is called a complex-conjugate pair.
If $z = a + ib$ (where $a, b$ are real numbers), the conjugate is: $ \bar{z} = a - ib $
Conjugates are obtained by changing the sign of the imaginary part, while the real part remains unchanged.
Modulus of a Complex Number
For $z = x + iy$, the modulus of complex zumber $z$, denoted by $|z|$, is the distance from the origin in the Argand plane: $|z| = \sqrt{x^2 + y^2}$
It is always a non-negative real number.
Every complex number can be represented as a point in the Argand plane with the $x$-axis as the real axis and the $y$-axis as the imaginary axis: $|z| = \sqrt{x^2 + y^2} = r$ where $r$ is the distance from the origin to the point $(x, y)$.
Square Root of a Complex Number
If $z = a + ib$, the square root of complex number $z$ is another complex number whose square equals $z$. If $\sqrt{z} = x + iy$, then: $(x + iy)^2 = a + ib$
The formula to find the square root is: $\sqrt{z} = \pm \left( \sqrt{\frac{|z| + \operatorname{Re}(z)}{2}} + i \sqrt{\frac{|z| - \operatorname{Re}(z)}{2}} \right)$
If $\operatorname{Im}(z) < 0$, the sign of the imaginary part is negative.
Algebraic Operations on Complex Numbers
This section explains the fundamental algebraic operations on complex numbers, including addition, subtraction, multiplication, and division.
Addition
Let $z_1 = a + ib$ and $z_2 = c + id$, then: $z_1 + z_2 = (a + c) + i(b + d)$
Example: $(2 + 3i) + (2 + 2i) = (2 + 2) + i(3 + 2) = 4 + 5i$
Subtraction
Let $z_1 = a + ib$ and $z_2 = c + id$, then: $z_1 - z_2 = (a - c) + i(b - d)$
Example: $(6 + 10i) - (10 + 3i) = (6 - 10) + i(10 - 3) = -4 + 7i$
Multiplication
Let $z_1 = a + ib$ and $z_2 = c + id$, then: $(a + ib)(c + id) = (ac - bd) + i(ad + bc)$
Example: $2i(2 + 6i) = (0 + 2i)(2 + 6i) = 0 + 12i^2 + 4i = -12 + 2i$
Division
Let $z_1 = c_1 + id_1$ and $z_2 = c_2 + id_2$, then the quotient is:
$\frac{z_1}{z_2} = z_1 \cdot \frac{1}{z_2}$
To divide, multiply $z_1$ by the reciprocal of $z_2$:
$\frac{z_1}{z_2} = z_1 \cdot \frac{\bar{z_2}}{|z_2|^2}$
Quadratic Equations
Solving quadratic equations means finding the value(s) of the variable that satisfy the equation. These values are called roots, solutions, or zeros. Since the degree of a quadratic equation is $2$, it can have a maximum of $2$ roots.
Example: For the equation $x^2 - 3x + 2 = 0$, we can see that $x = 1$ and $x = 2$ satisfy the equation, so these are its roots. But how do we find roots if they are not obvious?
There are several methods to solve quadratic equations:
Solving by factoring
Solving by completing the square
Solving by graphing
Solving using the quadratic formula
Nature of Roots
The nature of the roots of a quadratic equation depends on the discriminant $D = b^2 - 4ac$.
Real and Distinct Roots
$D > 0$
The curve intersects the $x$-axis at two distinct points.
Real and Equal Roots
$D = 0$
The curve intersects the $x$-axis at only one point.
Complex Roots
$D < 0$
The curve does not intersect the $x$-axis.
How to Find the Nature of Roots
Step 1: Compare the given quadratic equation with the standard form $ax^2 + bx + c = 0$ to find the coefficients $a$, $b$, and $c$.
Step 2: Substitute the coefficients into the discriminant: $D = b^2 - 4ac$ and solve.
Step 3: Determine the nature of the roots based on $D$:
If $D < 0$, the roots are complex
If $D = 0$, the roots are real and equal
If $D > 0$, the roots are real and distinct
| $b^2-4 a c$ $> 0$ | Real and unequal |
| $b^2-4 a c$ $= 0$ | Real and equal |
| $b^2-4 a c$ $< 0$ | Unequal and Imaginary |
| $b^2-4 a c$ $> 0$ (is a perfect square) | Real, rational and unequal |
| $b^2-4 a c$ $> 0$ (is not a perfect square) | Real, irrational and unequal |
| $b^2-4 a c$ $> 0$ (is aperfect square and $a$ or $b$ is irrational) | Irrational |
Sum and Product of Roots of a Quadratic Equation
Assume $\alpha$ and $\beta$ are the roots of a quadratic equation $ax^2 + bx + c = 0$.
Sum of Roots:
$\alpha + \beta = \frac{-b + \sqrt{D}}{2a} + \frac{-b - \sqrt{D}}{2a} $
$= \frac{-b}{2a} + \frac{\sqrt{D}}{2a} + \frac{-b}{2a} - \frac{\sqrt{D}}{2a} $
$= \frac{-2b}{2a} $
$= \frac{-b}{a} $
Product of roots:
$\alpha \cdot \beta = \frac{(-b + \sqrt{D})}{2a} \cdot \frac{(-b - \sqrt{D})}{2a} $
$= \frac{(-b)^2 - (\sqrt{D})^2}{(2a)^2} $
$= \frac{b^2 - D}{4a^2} $
$= \frac{b^2 - b^2 + 4ac}{4a^2} \quad [D = b^2 - 4ac] $
$= \frac{c}{a} $
A quadratic equation can be formed using the sum and product of roots:
$x^2 - (\alpha + \beta)x + (\alpha \cdot \beta) = 0 $
Location of Roots
Now let us look into the location of roots of quadratic equations.
Let $f(x) = ax^2 + bx + c$ where $a, b, c$ are real numbers and $a \neq 0$. Let $x_1$ and $x_2$ be the roots of $f(x)$ and let $k$ be any real number.
1. If both roots of $f(x)$ are less than $k$:
i) $D \ge 0$ (the roots may be distinct or equal)
ii) $a f(k) > 0$ (in both cases, $a f(k)$ is positive; if $a < 0$, then $f(k) < 0$, and multiplying two negative values gives a positive value)
iii) $k > -\frac{b}{2a}$ (since $-\frac{b}{2a}$ lies between $x_1$ and $x_2$, and $x_1, x_2 < k$, so $-\frac{b}{2a} < k$)
2. If both roots of $f(x)$ are greater than $k$:
i) $D \ge 0$
ii) $a f(k) > 0$
iii) $k < -\frac{b}{2a}$ (since $-\frac{b}{2a}$ lies between $x_1$ and $x_2$, and $x_1, x_2 > k$, so $-\frac{b}{2a} > k$)
Condition for a number $k$ with respect to the roots:
Let $f(x) = ax^2 + bx + c$ with real coefficients and $a \neq 0$.
Let $x_1$ and $x_2$ be the real roots of the quadratic equation.
Case (i): $k$ lies between the roots $x_1$ and $x_2$
i) $D \ge 0$
ii) $k_1 < -\frac{b}{2a} < k_2$, where $k_1 < k_2$
Case (ii): $k_1$ and $k_2$ lie between the roots
i) $a f(k_1) < 0$ and $a f(k_2) < 0$
Solved examples based on Complex Numbers and Quadratic Equations
Solution:
As we have learned
Polar Form of a Complex Number -
$z=r(\cos \theta+i \sin \theta)$
- wherein
$\mathrm{z}=$ modulus of z and $\theta$ is the argument of Z
Euler's Form of a Complex Number -
$z=r e^{i \theta}$
- wherein
r denotes the modulus of z and $\theta$ denotes the argument of z.
$z=x+i y=r(\cos \theta+i \sin \theta)$
$=r e^{i \theta}$
So, $\operatorname{Im} z^5=\operatorname{Im}\left(r e^{i \theta}\right)^5$
$=\operatorname{Im}\left(r^5 e^{i \theta 5}\right)$
$=r^5 \sin 50$
$(\operatorname{Im} z)^5=(r \sin \theta)^5$
$=\left(r^5 \sin ^5 \theta\right)$
So, $\frac{\operatorname{Im} z^5}{(\operatorname{Im} z)^5}=\frac{\sin 5 \theta}{\sin ^5 \theta}$
for minimum value, differentiating w.r.t $\theta$
So, $\frac{\sin ^5 \theta \cdot 5 \cos \theta-5 \sin 5 \theta \sin ^4 \theta \cos \theta}{\sin ^{10} \theta}$
$\Rightarrow \sin \theta \cdot \cos 5 \theta-\sin 5 \theta \cos \theta=0$
$
\begin{aligned}
& \Rightarrow \sin 4 \theta \cdot=0 \\
& 4 \theta=n \pi \\
& \theta=n \pi / 4
\end{aligned}
$
for $\mathrm{n}=1$
$\frac{\sin 5 \theta}{\sin ^5 \theta}=\frac{-1 / \sqrt{2}}{(1 / \sqrt{2})^5}=-4$
Hence, the answer is -4.
Solution:
Definition of Argument/Amplitude of z in Complex Numbers -
$\theta=\tan ^{-1}\left|\frac{y}{x}\right|, z \neq 0$
$\theta, \pi-\theta,-\pi+\theta,-\theta$ are Principal Arguments if z lies in the first, second, third, or fourth quadrant respectively.
$z=(1)^{\frac{1}{3}} \Rightarrow z=\cos \frac{2 k \pi}{3}+i \sin \frac{2 k \pi}{3}$
k=0,1,2 so z gives three roots
$\Rightarrow 1, \frac{-1}{2}+i \frac{\sqrt{3}}{2}(\omega), \frac{-1}{2}-i \frac{\sqrt{3}}{2}\left(\omega^2\right)$
- wherein
$\omega=\frac{-1}{2}+\frac{i \sqrt{3}}{2}, \omega^2=\frac{-1}{2}-\frac{i \sqrt{3}}{2}, \omega^3=1,1+\omega+\omega^2=0$
$1, \omega, \omega^2$ are cube roots of unity.
$x^2+x+1=0$, roots are, $\omega$ and $\omega^2$ where $\omega$ is the cube root of unity.
$
z=3+6 i\left(z_0\right)^{81}-3 i\left(z_0\right)^{90}
$
$z_0=\omega$ and $\omega^2$
$
\begin{aligned}
& z=3+6 i(\omega)^{81}-3 i(\omega)^{93} \\
& z=3+3 i \quad \because \omega^3=1 \\
& \arg (z)=\frac{1}{4}
\end{aligned}
$
Hence, the required answer is $\frac{\pi}{4}$.
Example 3: z is a complex number such that $z+\bar{z}=5$ and $z-\bar{z}=7 i$ then z equals
Solution:
We know the properties of the conjugate of a complex number:
$\operatorname{Im}(z) = \frac{z - \bar{z}}{2i}$, where
$\operatorname{Im}(z)$ denotes the imaginary part of $z$
$\bar{z}$ denotes the conjugate of $z$
$z + \bar{z} = 5$
$z - \bar{z} = 7i$
Adding both: $2z = 5 + 7i \Rightarrow z = \frac{5}{2} + \frac{7}{2}i$
Or, using formulas: $\operatorname{Re}(z) = \frac{z + \bar{z}}{2} = \frac{5}{2}$ and $\operatorname{Im}(z) = \frac{z - \bar{z}}{2i} = \frac{7}{2}$
Hence, the answer is $z = \frac{5}{2} + \frac{7}{2}i$
Example 4: z is a complex number such that $z-\bar{z}=4 i$ , then $\operatorname{Im}(z)$ equals
Solution:
As we learned in properties of the conjugate of a complex number:
$\operatorname{Im}(z) = \frac{z - \bar{z}}{2i}$ where $\operatorname{Im}(z)$ denotes the imaginary part of $z$
$\bar{z}$ denotes the conjugate of $z$
$\operatorname{Im}(z) = \frac{z - \bar{z}}{2i} = \frac{4i}{2i} = 2$
Hence, the answer is $2$.
Example 5: The multiplicative inverse of the complex number $z=\frac{5+i \sqrt{2}}{1-i \sqrt{2}}$ is:
Solution:
As we have learnt, the multiplicative inverse of $z$ is $\frac{1}{z}$
Now, $z = \frac{5+i \sqrt{2}}{1-i \sqrt{2}}$
$\frac{1}{z} = \frac{1-i \sqrt{2}}{5+i \sqrt{2}}$
$= \frac{1-i \sqrt{2}}{5+i \sqrt{2}} \cdot \frac{5-i \sqrt{2}}{5-i \sqrt{2}}$
$= \frac{5-i \sqrt{2}-i 5 \sqrt{2}-2}{25+2}$
$= \frac{3-6 \sqrt{2} i}{27}$
$= \frac{3(1-2 \sqrt{2} i)}{27}$
$= \frac{1-2 \sqrt{2} i}{9}$
So, the multiplicative inverse is $\frac{1-2 i \sqrt{2}}{9}$.
Hence, the answer is option 2.
List of Topics related to Complex Numbers according to NCERT/JEE MAIN
This section covers all essential topics on complex numbers as per NCERT and JEE Main syllabus. Understanding these topics thoroughly helps in solving a wide variety of problems in algebra, coordinate geometry, and higher-level mathematics.
NCERT Resources
Below provided are the NCERT Solutions, Exemplar problems, and concise notes for Class 11 Maths Chapter 5 – Complex Numbers and Quadratic Equations. These resources will help in understanding concepts and practising exam-relevant questions.
NCERT Solutions for Class 11 Maths Chapter 5 -Complex Numbers and Quadratic Equations
NCERT Exemplar Class 11 Maths Solutions for Chapter 5 - Complex Numbers and Quadratic Equations
NCERT Class 11 Maths Notes for Chapter 5 - Complex Numbers and Quadratic Equations
Recommended Books for Complex Numbers and Quadratic Equations
Here is a list of standard books that provide clear explanations, solved examples, and practice problems on complex numbers and quadratic equations, ideal for NCERT, JEE Main, and other competitive exams.
| Book Title | Author / Publisher | Description |
|---|---|---|
| NCERT Mathematics Textbook (Class 11) | NCERT | Official textbook with clear explanations, foundational concepts, and exercises on complex numbers and quadratic equations. Essential for board exam preparation. |
| Higher Algebra | Hall & Knight | A classic and comprehensive book on algebra, covering complex numbers and quadratic equations thoroughly for deeper understanding. |
| Algebra for JEE Main & Advanced | Arihant Publications | Includes theory, solved examples, and practice problems focused on complex numbers and quadratics tailored for JEE aspirants. |
| Complex Numbers and Quadratic Equations | M.L. Khanna | Detailed explanations and practice exercises specific to the topics with a focus on problem-solving techniques. |
| Problems in Algebra | V.L. Malakhov | Collection of varied difficulty problems on quadratic equations and complex numbers to enhance problem-solving skills. |
NCERT Subjectwise Resources
These NCERT resources cover each subject in a structured manner, offering theory, examples, and exercises that are essential for building a strong foundation in subjectwise key concepts.
| Resource | Mathematics | Physics | Chemistry |
|---|---|---|---|
| NCERT Notes | NCERT notes Class 11 Maths | NCERT notes Class 11 Physics | NCERT notes Class 11 Chemistry |
| NCERT Solutions | NCERT solutions for Class 11 Mathematics | NCERT solutions for Class 11 Physics | NCERT solutions for Class 11 Chemistry |
Practice Questions based on Complex Numbers and Quadratic Equations
These practice questions helps in boosting your understanding of complex numbers, including operations, conjugates, modulus, and quadratic equations, roots, allowing you to apply formulas and solve problems efficiently.
Frequently Asked Questions (FAQs)
A complex number is a number of the form $x + iy$, where $x$ and $y$ are real and $i = \sqrt{-1}$. A quadratic equation is a polynomial equation of degree 2, written as $ax^2 + bx + c = 0$.
A number of the form $x + iy$ is called a complex number.
The root is the value of $x$ that satisfies $ax^2 + bx + c = 0$, also called a solution or zero of the equation.
If the real part of the complex number is zero, then the complex number becomes a purely imaginary number. Eg. $0+2 i=2 i$
lota is an imaginary unit number that is denoted by $i$ and the value of iota is $\sqrt{-1}$ i.e., $i=\sqrt{-1}$. For analyzing the powers of iota, we calculate the first few powers of iota. i.e $i=\sqrt{-1}, i^2=-1, i^3=-\sqrt{-1}, i^4=1$
There are different ways of solving quadratic equations.
- Solving quadratic equations by factoring
- Solving quadratic equations by completing the square
- Solving quadratic equations by graphing
- Solving quadratic equations by quadratic formula