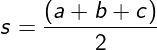1. Define Triangle.
A Triangle is a closed three-sided polygon with three vertices, three sides and three angles. It is a 2-dimensional structure made with three line segments joined together.
2. What are the different types of triangles?
Different types of triangles are
According to the measurement of angle:
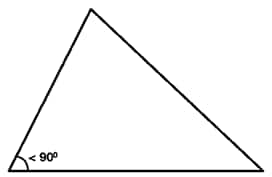
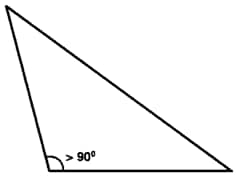
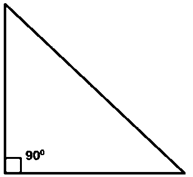
Acute angled triangle
Obtuse angled triangle
Right angled triangle
According to the side’s lengths:
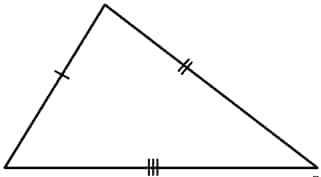
Scalene triangle
Isosceles triangle
Equilateral triangle
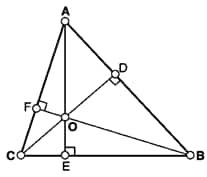
3. What are the different intersection points inside a triangle?
The different intersection points inside the triangle are
Orthocentre – Interaction point of all the three altitudes of the triangle.
Circumcentre – Interaction point of all the three perpendicular bisectors of the triangle.
Incentre – Interaction point of all the three angle bisectors of the triangle.
Centroid – Interaction point of all the three medians of triangle
4. What are the different properties of a triangle?
The different properties of a triangle are as follows:
Three vertices, three angles, and three sides make up a triangle.
Any two triangle sides when added together have a length larger than the third side.
Difference between the lengths of the two sides of the triangle is less than the third side.
Sum of all the angles of the triangle is 180°, also known as the angle sum property.
The Triangle’s total exterior sum is 360°.
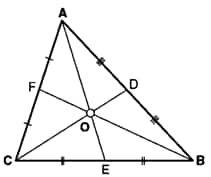
5. Define median and altitude of the triangle.
Median: - A line segment drawn from the vertex and joining the midpoint of the opposite side of the triangle is known as the median of the triangle.
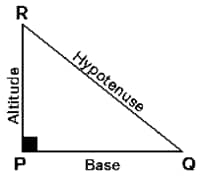
Altitude:- Line drawn from the vertex of the triangle and ends at the opposite side making a right angle is known as the altitude of the triangle.
6. What is the altitude of a triangle?
The altitude of a triangle is a line segment from a vertex perpendicular to the opposite side (or its extension). It's the shortest distance from a vertex to the opposite side.
7. How many altitudes does a triangle have?
Every triangle has three altitudes, one from each vertex to the opposite side.
8. How can you construct an altitude of a triangle using only a straightedge and compass?
To construct an altitude, draw a perpendicular line from a vertex to the opposite side using the perpendicular line construction method with a compass and straightedge.
9. How do altitudes help in determining if a triangle is acute, right, or obtuse?
If all altitudes lie inside the triangle, it's acute. If one altitude coincides with a side, it's right. If an altitude falls outside, it's obtuse.
10. How does the concept of altitude relate to trigonometry?
Altitudes are crucial in trigonometry, especially in defining sine and cosine. The sine of an angle in a right triangle is the ratio of the opposite side (an altitude) to the hypotenuse.
11. What is the relationship between the altitudes and the area of a triangle?
The area of a triangle can be calculated using any side as the base and its corresponding altitude as the height: Area = (1/2) × base × altitude. This means that the product of any side and its altitude is constant for a given triangle.
12. How can the concept of altitude be used to solve real-world problems?
Altitudes are used in various real-world applications, such as measuring the height of buildings or mountains, calculating the trajectory of projectiles, or determining the slope of a roof.
13. What is the difference between an altitude and a height of a triangle?
The terms are often used interchangeably, but strictly speaking, the altitude is the line segment, while the height is the length of that line segment.
14. How do altitudes and medians relate to the concept of triangle congruence?
While equal altitudes or medians alone don't guarantee congruence, they can be used in combination with other information to prove triangle congruence in certain cases.
15. How do altitudes relate to the concept of similarity in triangles?
If two triangles are similar, their corresponding altitudes are proportional to their corresponding sides. This property is often used in solving advanced geometry problems.
16. What is the orthocenter of a triangle?
The orthocenter is the point where all three altitudes of a triangle intersect. In an acute triangle, it's inside; in a right triangle, it's at the right angle; and in an obtuse triangle, it's outside.
17. What is the centroid of a triangle?
The centroid is the point where all three medians of a triangle intersect. It divides each median in a 2:1 ratio, with the longer segment closer to the vertex.
18. What is the nine-point circle of a triangle?
The nine-point circle is a circle that passes through nine significant points of a triangle, including the midpoints of the three sides and the feet of the three altitudes.
19. What is the Euler line in a triangle?
The Euler line is a straight line that passes through several important points in a triangle, including the orthocenter, centroid, and circumcenter.
20. What is the relationship between the centroid and the vertices of a triangle?
The centroid divides each median into two segments, with the segment closer to the vertex being twice the length of the segment closer to the midpoint of the opposite side.
21. What is the median of a triangle?
The median of a triangle is a line segment that connects a vertex to the midpoint of the opposite side. It divides the triangle into two equal areas.
22. Can a median be perpendicular to a side of the triangle?
Yes, in an isosceles triangle, the median to the base is perpendicular to the base and bisects the vertex angle.
23. What is the relationship between the medians and the sides of an equilateral triangle?
In an equilateral triangle, all medians are equal in length and bisect each other. They are also altitudes and angle bisectors.
24. What is the theorem of the three medians?
The theorem of the three medians states that the three medians of a triangle intersect at a single point (the centroid) which divides each median in a 2:1 ratio.
25. How can the concept of median be used to find the area of a quadrilateral?
By drawing the diagonals of a quadrilateral, you create four triangles. The medians of these triangles can be used to calculate their areas, which sum to the quadrilateral's area.
26. What is the relationship between the medians and the perimeter of a triangle?
There's no direct relationship between the lengths of the medians and the perimeter. However, the sum of the squares of the medians is three-fourths the sum of the squares of the sides.
27. How does the position of the orthocenter change as the triangle changes from acute to obtuse?
As a triangle changes from acute to right to obtuse, the orthocenter moves from inside the triangle to the right angle vertex, and then outside the triangle.
28. Can a triangle have two equal altitudes without being isosceles?
No, if a triangle has two equal altitudes, it must be isosceles. Equal altitudes imply equal angles opposite to them, which in turn implies two equal sides.
29. What is the relationship between the lengths of the medians in an equilateral triangle?
In an equilateral triangle, all medians are equal in length. The length of each median is √3/2 times the length of a side.
30. What is the centroid theorem?
The centroid theorem states that the centroid divides each median into two segments, with the segment closer to the vertex being twice the length of the segment closer to the midpoint of the opposite side.
31. What is the relationship between the orthocenter and the centroid?
The orthocenter and centroid lie on the Euler line. The centroid is located 1/3 of the way from the midpoint of each side to the opposite vertex, while the orthocenter can be inside, on, or outside the triangle.
32. Can an altitude be outside the triangle?
Yes, in an obtuse triangle, two of the altitudes will fall outside the triangle because the perpendicular line to the extended side doesn't intersect within the triangle's boundaries.
33. How does the altitude relate to the area of a triangle?
The area of a triangle can be calculated using the formula: Area = (1/2) × base × height, where height is the length of the altitude perpendicular to the base.
34. Can a side of a triangle be its own altitude?
Yes, in a right triangle, the two sides forming the right angle are altitudes to each other.
35. What happens to the altitudes as a triangle becomes more obtuse?
As a triangle becomes more obtuse, two of its altitudes become longer and fall outside the triangle, while the third becomes shorter.
36. How does the concept of altitude apply to area comparisons between triangles?
Two triangles with the same base and height (altitude) have equal areas, even if they have different shapes. This concept is crucial in comparing and proving area equivalences.
37. How many medians does a triangle have?
Every triangle has three medians, one from each vertex to the midpoint of the opposite side.
38. What's the difference between an altitude and a median?
An altitude is perpendicular to the opposite side, while a median connects a vertex to the midpoint of the opposite side. Altitudes measure height, while medians divide the triangle into equal areas.
39. How do medians relate to the area of a triangle?
Each median divides the triangle into two equal areas. This property is used in some advanced area calculations and proofs.
40. What is the relationship between the length of a median and the sides of a triangle?
The length of a median (m) to side a in a triangle with sides a, b, and c is given by the formula: m² = (1/4)(2b² + 2c² - a²)
41. Can an altitude and a median coincide?
Yes, in an isosceles triangle, the altitude to the base, the median to the base, and the angle bisector to the base all coincide.
42. How do the concepts of altitude and median contribute to the study of triangle inequalities?
Altitudes and medians are used in various triangle inequalities. For example, the sum of the squares of two sides of a triangle is equal to twice the square of the median to the third side plus half the square of the third side. Such relationships help in proving and understanding more complex geometric inequalities.
43. How do the concepts of altitude and median relate to the idea of symmetry in triangles?
In isosceles triangles, the altitude and median to the base coincide and form a line of symmetry. In equilateral triangles, all altitudes and medians coincide and form three lines of symmetry.
44. Can the orthocenter and centroid coincide? If so, under what conditions?
The orthocenter and centroid coincide only in an equilateral triangle. In this case, they also coincide with the incenter and circumcenter, forming the single point known as the triangle center.
45. What is the relationship between the orthocenter and the vertices in an acute triangle?
In an acute triangle, the orthocenter and the three vertices form three new triangles, each similar to the original triangle.
46. How does the concept of altitude apply to non-Euclidean geometry?
In non-Euclidean geometries like spherical or hyperbolic geometry, the concept of altitude still exists but may have different properties. For example, on a sphere, "straight" lines are great circles, changing how we define perpendicularity.
47. What is the role of altitudes in the study of triangle centers?
Altitudes play a crucial role in defining several important triangle centers, including the orthocenter (intersection of altitudes) and the nine-point center (center of the nine-point circle, which is related to the feet of the altitudes).
48. How do medians relate to the concept of balance in physics?
The centroid, where the medians intersect, is the center of mass of a triangular plate of uniform density. This concept is important in physics and engineering for understanding balance and stability.
49. How do medians relate to the concept of center of gravity in physics?
The intersection point of the medians (the centroid) is the center of gravity of a triangular plate. This is why a triangular object balanced on its centroid will remain stable.
50. How does the concept of altitude apply to triangles drawn on a sphere?
On a sphere, an altitude is still perpendicular to the opposite side, but "straight" lines are great circles. The altitude is the shortest arc from a vertex perpendicular to the opposite side along a great circle.
51. How can the concept of median be used in computer graphics or game design?
Medians are useful in computer graphics for tasks like triangulation of polygons, mesh generation, and creating balanced designs. They're also used in algorithms for efficient searching and sorting of triangular data structures.
52. What is the role of altitudes in the study of conic sections?
Altitudes play a role in defining and studying conic sections. For example, in a parabola, the distance from any point to the focus is equal to its distance from the directrix, which is measured along an altitude to the directrix.
53. What is the relationship between the altitudes of a triangle and its inscribed circle?
The altitudes of a triangle are closely related to its inscribed circle. The point where the altitudes intersect (orthocenter) is used in constructing the nine-point circle, which is externally tangent to the inscribed circle.
54. How can the concept of median be applied to data analysis and statistics?
While not directly related to triangle medians, the statistical median (middle value in a dataset) shares the concept of dividing a set into equal parts. Understanding geometric medians can help in grasping statistical concepts.
55. What is the relationship between the altitudes and the circumcircle of a triangle?
The feet of the altitudes lie on the circumcircle of the medial triangle (triangle formed by connecting the midpoints of the original triangle's sides). This circle is known as the nine-point circle and has half the radius of the original triangle's circumcircle.
![]()
![]()
![]()