Area of Similar Triangles - Formula, Theorem, Proof, Examples

Edited By Team Careers360 | Updated on Jul 02, 2025 05:14 PM IST

Similar triangles are defined as that type of triangles that have the same shape, but their sizes may differ. In equilateral triangles, the squares of any side length are examples of similar objects or triangles. In other words, if any two triangles are similar, then their corresponding angles are also congruent and corresponding sides are also in equal proportion. The similarity of triangles here given by the ‘~’ symbol.

This Story also Contains

Introduction
Properties Of Similar Triangles
Formulas
Similar Triangles Vs Congruent Triangles
Similar Triangles Theorems With Proofs
Area Of Similar Triangles Theorem

Introduction

If any two triangles are similar, they always have the same ratio of corresponding sides and also equal pair of corresponding angles.

If any two or more figures have the same shape, but their sizes may differ, then these objects are known as similar figures.

Triangle is also known as a three-sided polygon. The condition is for only the similarity of triangles is;

In a similar triangle the corresponding angles of both triangles are equal, and
In a similar triangle corresponding sides of both triangles are always proportional to each other.

Properties Of Similar Triangles

Reflexivity: It is defined when A triangle (△) is similar to itself.
Symmetry: Symmetry is defined when △ ABC ∼ △ DEF, Then △ DEF ∼ △ ABC
Transitivity: Transitivity is defined when △ ABC ∼△ DEF and△ DEF ∼△ XYZ, then △ ABC ∼△ XYZ
Both triangles have the same shape but sizes may differ.
Each pair of corresponding angles of a triangle are always equal
The ratio of corresponding sides of a triangle is the same

Formulas

According to the definition, when two triangles are similar and their corresponding angles are congruent and their corresponding sides are always proportional. We can also find the dimensions of any one triangle with the help of another triangle. Now, let us consider ABC and XYZ are two similar triangles, then with the help of the given formulas, relevant angles and side lengths can be found out.

\angle\:A=\angle\:B,\angle\:B=\angle\:C,\angle\:C=\angle\:Z

NEET Highest Scoring Chapters & Topics

This ebook serves as a valuable study guide for NEET exams, specifically designed to assist students in light of recent changes and the removal of certain topics from the NEET exam.

Download E-book

AB\div\:XY=BC\div\:YZ=AC\div\:XZ

Similar Triangles Vs Congruent Triangles

The comparison of similar and congruent triangles is given below in the table.

Similar Triangles	Congruent Triangles
Similar triangles have only same shape but are different in size	Congruent triangles have the same shape and same size
The symbol is ‘~’	The symbol is ‘≅’
The ratio of all the corresponding sides are same	The ratio of corresponding sides is always equal to a constant value

Similar Triangles Theorems With Proofs

AA (or AAA) or Angle-Angle Similarity
SAS or Side-Angle-Side Similarity
SSS or Side-Side-Side Similarity

1)AA (or AAA) or Angle-Angle Similarity

If two angles of a triangle are equal to any two angles of another triangle, then the two triangles are similar to each other; this means the triangle has Angle-Angle Similarity.

2) SAS or Side-Angle-Side Similarity

If any two sides of a triangle are in the same proportion as of the two sides of another triangle, and that angle is inscribed by the two sides in both triangles are equal, then two triangles are said to be Side-Angle-Side similarity.

3) SSS or Side-Side-Side Similarity

If all three sides of a triangle are in proportion to the three sides of another triangle, then these two triangles are called to be Side-Side-Side similar.

Area Of Similar Triangles Theorem

According to the similar triangle, the theorem states that If any two triangles are similar, then the ratio of the area of both triangles will be proportional to the square of the ratio of corresponding sides.

To prove this theorem, Let us consider two similar triangles \triangle\:ABC and \triangle\:PQR

According to this theorem,

\frac{area\:of\triangle\:ABC}{area\:of\triangle\:PQR}

=\frac{\lgroup\:AB\rgroup^{2}}{\lgroup\:PQ\rgroup^{2}}

=\frac{\lgroup\:BC\rgroup^{2}}{\lgroup\:QR\rgroup^{2}}

=\frac{\lgroup\:CA\rgroup^{2}}{\lgroup\:RP\rgroup^{2}}

We know that,

Area of triangle = \frac{1}{2}\times\:base\times\:height

To find the area of \triangle\:ABC and \triangle\:PQR

, first draw the altitudes AD and PE from the vertex A and P of \triangle\:ABC and \triangle\:PQR respectively, as shown in the figure -

Now, area of ΔABC =

\frac{1}{2}\times\:BC\times\:AD

area of \triangle\:PQR

=\frac{1}{2}\times\:QR\times\:PE

The ratio of the areas of both triangles is given by:

\frac{area\:of\triangle\:ABC}{area\:of\triangle\:PQR}

=\frac{\frac{1}{2}\times\:BC\times\:AD}{\frac{1}{2}\times\:QR\times\:PE}

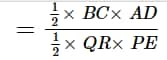
1706370226009

\frac{area\:of\triangle\:ABC}{area\:of\triangle\:PQR} =

=\frac{BC\times\:AD}{QR\times\:PE}

……………. (1)

Now in \triangle\:ABD and \triangle\:PQE

it can be seen that:

\angle\:ABC = \angle\:PQR (Since \triangle\:ABC \sim\triangle\:PQR )

\angle\:ABD = \angle\:PEQ (Since both the angles are 90°)

From AA criterion of similarity \triangle\:ADB \sim\triangle\:PEQ

\Rrightarrow\frac{AD}{PE}=\frac{AB}{PQ} …………….(2)

Since it is known that \triangle\:ABC \sim\triangle\:PQR

=\frac{AB}{PQ}=\frac{BC}{QR}=\frac{AC}{PR} …………….(3)

Now, substitute the value in equation (1), we get

\frac{area\:of\triangle\:ABC}{area\:of\triangle\:PQR} =

=\frac{AB}{PQ}\times\frac{AD}{PE}

Using equation (2), we have-

\frac{area\:of\triangle\:ABC}{area\:of\triangle\:PQR} =

=\frac{AB}{PQ}\times\frac{AB}{PQ} \frac{area\:of\triangle\:ABC}{area\:of\triangle\:PQR} =

=\lgroup\:\frac{AB}{PQ}\rgroup^{2}

Also from equation (3) we have-

\frac{area\:of\triangle\:ABC}{area\:of\triangle\:PQR} =

=\lgroup\:\frac{BC}{QR}\rgroup^{2}

=\lgroup\:\frac{CA}{RP}\rgroup^{2}

This proves that the ratio of the area of two similar triangles is always proportional to the squares of the corresponding sides of both triangles.

Frequently Asked Questions (FAQs)

1. Define similar triangles?

Two triangles are said to be similar if they have the same ratio of corresponding sides and equal pairs of corresponding angles.

2. What is the symbol for similar triangles?

If ABC and PQR are two similar triangles, then these two triangles are represented by:
∆ABC ~ ∆PQR

3. Are similar triangles and congruent triangles the same?

No, a similar triangle and the congruent triangle are not the same. Similar triangles have the same shape but sizes may vary on the other hand, congruent triangles have the same shape and size.

4. What are three similar theorems for triangles?

The three similarities theorem are given below:
1. Angle-angle (AA)
2. Side-angle-side (SAS)
3. Side-side-side (SSS)

5. What are the 2 situations in which a triangle can be similar?

The two triangles are said to be similar if they have:

All their angles are equal.
And their corresponding sides of triangles are in the same ratio.

6. What's the relationship between the perimeter ratio and area ratio of similar triangles?

While the ratio of the perimeters of similar triangles is equal to the ratio of their corresponding sides, the ratio of their areas is equal to the square of this ratio. This means the area ratio is always greater than the perimeter ratio (except when the ratio is 1:1).

7. How does the area of similar triangles theorem relate to the concept of scale factor?

The scale factor is the ratio of corresponding sides in similar triangles. The area of similar triangles theorem states that the ratio of their areas is equal to the square of this scale factor. For example, if the scale factor is 2, the ratio of areas will be 2² = 4.

8. How does changing one side of a triangle affect its area in relation to a similar triangle?

If you change one side of a triangle while maintaining similarity with another triangle, the area will change by the square of the change in the side length. For example, if you double a side length, the area will increase by a factor of 4.

9. How does the area of similar triangles theorem relate to the concept of dilation in geometry?

Dilation is a transformation that produces a similar figure. The area of similar triangles theorem directly relates to dilation: if a triangle is dilated by a scale factor k, its area will be multiplied by k². This is because dilation affects both dimensions of the triangle simultaneously.

10. What common misconceptions do students have about the area of similar triangles?

Common misconceptions include thinking that the ratio of areas is the same as the ratio of sides, forgetting to square the ratio of sides, or assuming that doubling the sides will double the area. Understanding that area is a two-dimensional measure is key to avoiding these misconceptions.

11. How does the area of similar triangles theorem help in understanding the concept of scale in maps?

The theorem is crucial in cartography. When a map is created, it's a scaled-down version of the actual land area. The scale factor of the map relates to the linear dimensions, but the area ratio follows the squared relationship. This helps cartographers accurately represent and calculate areas on maps.

12. What role does the area of similar triangles theorem play in fractal geometry?

In fractal geometry, shapes are often composed of smaller, similar versions of themselves. The area of similar triangles theorem helps in understanding how the areas of these self-similar shapes relate to each other at different scales, which is crucial in analyzing fractal dimensions and properties.

13. Can you explain how the area of similar triangles theorem might be used in computer graphics or digital imaging?

In computer graphics and digital imaging, scaling images while maintaining proportions is crucial. The theorem helps in understanding how the number of pixels (which represent area) changes when an image is scaled. If an image is scaled up by a factor of 2, for instance, the number of pixels will increase by a factor of 4.

14. How does the area of similar triangles theorem help in understanding the concept of similarity in three-dimensional objects?

While the theorem directly applies to two-dimensional triangles, it helps in understanding the relationship between similar three-dimensional objects. For 3D objects, the ratio of surface areas follows the square relationship (like the areas of triangles), while the ratio of volumes follows a cubic relationship.

15. What's the significance of the area of similar triangles theorem in architectural design?

In architecture, this theorem is crucial for scaling designs. When architects create models or scaled drawings, they use this principle to ensure that areas in the model accurately represent the areas in the full-scale building. It's essential for maintaining proportions and calculating material requirements.

16. What's the connection between the area of similar triangles theorem and the Pythagorean theorem?

While these theorems address different aspects of triangles, they're both based on squared relationships. The Pythagorean theorem relates the squares of side lengths in a right triangle, while the area of similar triangles theorem relates the squares of scale factors to area ratios. Both demonstrate the importance of squared relationships in geometry.

17. How does the area of similar triangles theorem relate to the concept of proportionality in mathematics?

The theorem is a perfect example of proportionality, specifically squared proportionality. It shows that while linear dimensions (sides) of similar triangles are directly proportional, their areas are proportional to the square of this ratio. This illustrates how proportionality can behave differently in different dimensions.

18. How does the area of similar triangles theorem help in understanding the concept of scale invariance?

Scale invariance is a property where features of an object or system remain similar regardless of scale. The area of similar triangles theorem demonstrates a specific type of scale invariance: while the absolute sizes change, the proportional relationships (squared for areas) remain constant across different scales.

19. What's the connection between the area of similar triangles theorem and the concept of self-similarity in nature?

Self-similarity, where an object is similar to part of itself, is common in nature (e.g., in ferns or coastlines). The area of similar triangles theorem helps explain how these self-similar structures scale. Each smaller part has an area related to the square of its linear dimension compared to the whole, maintaining the same patterns at different scales.

20. How does the area of similar triangles theorem help in understanding the concept of scaling laws in physics?

Scaling laws describe how physical quantities change with size. The area of similar triangles theorem is a perfect example of a scaling law: it shows how area scales with the square of linear dimension. This principle extends to other physical properties, helping physicists understand how different quantities scale relative to each other as objects or systems change size.

21. How does the area of similar triangles theorem relate to the concept of similarity?

The area of similar triangles theorem is a direct consequence of similarity. When two triangles are similar, their corresponding angles are equal, and their sides are proportional. This proportionality extends to their areas, but with a squared relationship due to area being a two-dimensional measure.

22. What is the fundamental principle behind the area of similar triangles?

The fundamental principle is that the ratio of the areas of similar triangles is equal to the square of the ratio of their corresponding sides. This means that if two triangles are similar, their areas are proportional to the square of the scale factor between their sides.

23. Why is the ratio of areas of similar triangles squared, while the ratio of their sides is not?

The ratio of areas is squared because area is a two-dimensional measure, while side length is one-dimensional. When you scale a triangle, you're increasing both its length and width, which results in a squared effect on the area.

24. Can you explain the formula for the area of similar triangles?

The formula for the area of similar triangles is: A₁/A₂ = (s₁/s₂)², where A₁ and A₂ are the areas of the two similar triangles, and s₁ and s₂ are any corresponding sides of the triangles. This formula shows that the ratio of the areas is equal to the square of the ratio of corresponding sides.

25. How can you prove the area of similar triangles theorem?

The proof involves showing that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. This can be done using the formula for the area of a triangle (A = ½bh) and the properties of similar triangles, particularly the proportionality of their sides.

26. Can you explain why the area ratio of similar triangles is always greater than or equal to 1?

The area ratio of similar triangles is always greater than or equal to 1 because we conventionally express it as the ratio of the larger triangle's area to the smaller triangle's area. Even if the triangles are identical, the ratio would be 1. If they're different sizes, the larger triangle will always have a greater area, resulting in a ratio greater than 1.

27. What's the significance of the area of similar triangles theorem in real-world applications?

This theorem is crucial in various fields such as architecture, engineering, and cartography. It allows for accurate scaling of designs and maps, and helps in calculating areas of objects or land parcels that are not directly measurable but are similar to known shapes.

28. What role does the area of similar triangles theorem play in understanding the concept of fractional dimensions?

While the theorem deals with whole number dimensions (1D for length, 2D for area), it helps in conceptualizing fractional dimensions. In fractal geometry, some shapes have dimensions between 1 and 2, or 2 and 3. The theorem provides a basis for understanding how these fractional dimensions relate to scaling properties.

29. How can you use the area of similar triangles theorem to find the area of a triangle that's difficult to measure directly?

If you have a triangle that's difficult to measure, you can create a similar, smaller triangle that's easier to measure. Once you know the area of the smaller triangle and the ratio of corresponding sides between the two triangles, you can use the theorem to calculate the area of the larger triangle.

30. How can you use the area of similar triangles theorem to solve problems involving indirect measurements?

The theorem is useful for indirect measurements when direct measurement is impractical. For example, you could use it to calculate the area of a large, inaccessible triangular plot of land by measuring a similar, smaller triangle and using the known ratio between their corresponding sides.

31. How can the area of similar triangles theorem be used to explain why small animals lose heat faster than large animals?

This theorem helps explain the surface area to volume ratio in biology. As an animal increases in size, its surface area (which follows the squared relationship) increases more slowly than its volume (which follows a cubic relationship). This means smaller animals have a larger surface area relative to their volume, leading to faster heat loss.

32. What role does the area of similar triangles theorem play in the field of computer-aided design (CAD)?

In CAD, this theorem is crucial for scaling designs accurately. When a design is scaled up or down, the software uses this principle to ensure that areas are scaled correctly in relation to linear dimensions. This is essential for maintaining proportions and accurately representing sizes in different views or scales.

33. How does the area of similar triangles theorem relate to the concept of isoperimetric inequality?

The isoperimetric inequality states that among all shapes with a given perimeter, the circle encloses the maximum area. The area of similar triangles theorem helps in understanding why this is true: as shapes become more "circular," they enclose more area for a given perimeter, following the squared relationship between linear measure (perimeter) and area.

34. How can the area of similar triangles theorem be used to explain why small drops of liquid tend to be more spherical than large ones?

This theorem helps explain surface tension effects. In a liquid drop, surface tension tries to minimize surface area relative to volume. As drops get smaller, their surface area (which scales with the square of radius) decreases more rapidly than their volume (which scales with the cube of radius), making it easier for surface tension to pull them into a spherical shape.

35. How does the area of similar triangles theorem relate to the concept of dimensional homogeneity in physics equations?

Dimensional homogeneity requires that all terms in a physical equation have the same dimensions. The area of similar triangles theorem illustrates this principle: both sides of the equation A₁/A₂ = (s₁/s₂)² are dimensionless ratios, maintaining dimensional homogeneity. This concept is crucial in deriving and checking the validity of physical equations.

36. Can the area of similar triangles theorem be applied to other similar shapes?

Yes, the principle behind this theorem extends to all similar shapes. For any similar two-dimensional figures, the ratio of their areas is always equal to the square of the ratio of their corresponding linear dimensions.

37. What's the relationship between the area of similar triangles theorem and the concept of dimensional analysis?

The theorem illustrates a key principle in dimensional analysis: when scaling between similar shapes, area (a two-dimensional measure) scales with the square of the linear dimension. This principle extends to other dimensions as well, helping to understand how different physical quantities scale relative to each other.

38. How does the area of similar triangles theorem relate to the concept of geometric mean?

The geometric mean of two numbers is the square root of their product. In similar triangles, the ratio of areas is the square of the ratio of corresponding sides. This means that the ratio of sides is the geometric mean of the ratio of areas, illustrating a connection between these concepts.

39. Can you explain how the area of similar triangles theorem might be used in physics, particularly in optics?

In optics, this theorem is useful in understanding image formation by lenses and mirrors. The size of an image formed by a lens is similar to the object, and the ratio of their areas is related to the square of the magnification. This helps in calculating image sizes and intensities in optical systems.

40. What's the connection between the area of similar triangles theorem and the concept of quadratic growth?

The area of similar triangles theorem is a geometric representation of quadratic growth. As the sides of a triangle increase linearly, the area increases quadratically (as the square of the side length). This parallels how quadratic functions behave, where the output grows as the square of the input.

41. How can the area of similar triangles theorem be used to explain why doubling the radius of a circle quadruples its area?

While this theorem is about triangles, the principle extends to all similar shapes. A circle can be thought of as a polygon with infinitely many sides. When you double the radius, you're effectively doubling all these "sides," which results in quadrupling the area, just as the theorem predicts for similar shapes.

42. How does the area of similar triangles theorem relate to the concept of power laws in mathematics and science?

The theorem is an example of a power law relationship, specifically a square law. Power laws describe relationships where one quantity varies as a power of another. In this case, area varies as the square of linear dimension. This concept extends to many natural and social phenomena, making it a fundamental principle in various scientific fields.

43. Can you explain how the area of similar triangles theorem might be applied in financial modeling or economics?

In economics, this theorem can help understand concepts like economies of scale. For instance, as a company grows (increasing its 'size' linearly), its efficiency or output might grow quadratically, similar to how the area of a triangle grows in relation to its sides. This can help model how companies benefit from increased size.

44. How does the area of similar triangles theorem help in understanding the concept of allometric scaling in biology?

Allometric scaling refers to how biological variables scale with body size. The area of similar triangles theorem helps explain why certain biological characteristics (like metabolic rate) don't scale linearly with body mass. Instead, they often scale with exponents related to surface area (square) or volume (cube) ratios, which this theorem helps illustrate.

45. What's the significance of the area of similar triangles theorem in the field of material science, particularly in nanotechnology?

In nanotechnology, as materials are scaled down, their surface area to volume ratio increases dramatically. This theorem helps explain why nanomaterials often have very different properties from their larger counterparts. The squared relationship of area to linear dimension is crucial in understanding these scale-dependent properties.

46. How can the area of similar triangles theorem be used to explain the concept of wind resistance in physics?

Wind resistance is proportional to the cross-sectional area of an object. The theorem helps explain why doubling the size of an object increases its wind resistance by a factor of four. This has implications in various fields, from automotive design to understanding the locomotion of different-sized animals.

47. Can you explain how the area of similar triangles theorem might be used in urban planning or landscape architecture?

In urban planning and landscape architecture, this theorem is useful for scaling designs and understanding space utilization. For example, when designing parks or public spaces, planners can use this principle to understand how doubling the linear dimensions of a space will quadruple its area, affecting capacity, resource requirements, and overall layout.

48. Can you explain how the area of similar triangles theorem might be applied in the field of acoustics or sound engineering?

In acoustics, this theorem helps understand how sound intensity changes with distance. Sound spreads out spherically, and the surface area of a sphere follows the squared relationship with its radius. This is why sound intensity decreases with the square of the distance from the source, following the same principle as the area of similar triangles.

49. What role does the area of similar triangles theorem play in understanding the concept of mechanical advantage in simple machines?

The theorem helps explain the trade-off between force and distance in simple machines like levers. When you increase the length of a lever arm, you increase the distance moved but decrease the force needed, following a squared relationship. This is analogous to how changing the sides of a triangle affects its area.

50. What's the significance of the area of similar triangles theorem in understanding the concept of scale invariance in phase transitions?

In physics, some phase transitions exhibit scale invariance, where the system looks similar at different scales. The area of similar triangles theorem provides a simple model for understanding how properties might scale during these transitions, helping physicists develop and understand more complex models of critical phenomena.