What is Altitude of a Triangle? Definition, Formulas and Examples

The Altitude of a Triangle

Edited By Team Careers360 | Updated on Jul 02, 2025 05:16 PM IST

The altitude of a triangle is the perpendicular drawn from the vertex of a triangle to the opposite side. As there are only three sides in a triangle, therefore only three perpendiculars can be drawn in it on a side from opposite vertices. Different triangles have different kinds of altitudes. The height of a triangle is used in calculating the area of a triangle. This height or length of perpendicular is generally denoted by the letter' h'.

This Story also Contains

Properties of Altitude of a Triangle
The altitude of a Triangle Formula
Height of a Scalene Triangle
Altitudes of Different Triangles
The altitude of an Equilateral Triangle
The altitude of an Isosceles Triangle
The altitude of a right-angled triangle-
The formulas for the altitude are summed up in the following table.
Difference Between Median and Altitude of Triangle

The Altitude of a Triangle

Properties of Altitude of a Triangle

• A triangle can have three altitudes.

• The altitudes can be within or outside the triangle which is depended upon the type of triangle.

• The altitude makes an angle of 90 ° to the opposite side of the triangle to it.

• The point of intersection of the three altitudes of a triangle is said to be the orthocenter of the triangle.

The altitude of a Triangle Formula

The formula we use to find the area of a triangle is given below-

$A=\frac{1}{2}*B*H$ (here the H represents the altitude and B represents the base).

Using this formula, we can calculate the height( altitude) of a triangle

$Altitude=\frac{\lgroup 2*Area\rgroup}{Base}$

Height of a Scalene Triangle

In the scalene triangle, all three sides are of different lengths. therefore, we get three different heights or lengths of altitudes corresponding to each side.

To find the altitude or height of a scalene triangle, we use Heron's formula which is given below-

$h=2\sqrt{s}[s-a][s-b][s-c]bh=2s[s-a][s-b][s-c]$

Here , h is the height or altitude of the triangle,

s is the semi- perimeter;

a, b, and c are the sides of the triangle.

The path to deciding the formula for the altitude of a scalene triangle is as follows

• Using Heron's formula the area of a triangle will be equal to

$A=2\sqrt{s}[s-a][s-b][s-c]$

$A={s}[s-a][s-b][s-c]$

• The formula to find the area of a triangle with respect to its base' B ' and altitude' H ' is

$A=\frac{1}{2}*B*H$

• If we place both the area formulas the same, so, we get,

$\frac{1}{2}*b*h=\sqrt{s. \left ( s-a \right ) .\left ( s-b \right ).\left ( s-c \right )}$

• Hence, the altitude of a scalene triangle is

$h=\frac{2\sqrt{s. \left ( s-a \right ) .\left ( s-b \right ).\left ( s-c \right )}}{b}$

Altitudes of Different Triangles

Regarding altitude, in different triangles, there will be different types of altitude.

For an obtuse-angled triangle, two altitudes are outside and one inside the triangle.

For an acute angled triangle, all three altitudes are inside the triangle.

For a right-angled triangle, the perpendicular sides are altitudes for each other, while the altitude on the hypotenuse is inside the triangle.

The altitude of an Equilateral Triangle

A triangle in which all three sides are equal is said to be an equilateral triangle.

As all three sides and angles are equal in an equilateral triangle, all the altitudes of an equilateral triangle are also equal.
In an equilateral triangle, altitude, median, and angle bisector are all given by the same line.
The length of altitude of an equilateral triangle with side ‘a’ is given by (√3/2)a.

The altitude of an Isosceles Triangle

An isosceles triangle is a triangle in which two sides are equal. The altitude of an isosceles triangle is vertical to its base.

In an isosceles triangle, the altitudes on the equal sides are equal in length.
In an isosceles triangle, the altitude, median, and angle bisector from the common vertex of equal sides are represented by same line.
The length of this altitude is given by h = √(a2 - (b2/4)), where a is the length of equal sides and b is the length of third side, and h is the length of altitude corresponding to the third (unequal) side.

The altitude of a right-angled triangle-

It divides the triangle into two same triangles.

From the right triangle altitude theorem, the altitude on the hypotenuse is always equal to the geometric mean of line segments formed by altitude on the hypotenuse

In a right triangle, when a perpendicular is drawn from the vertex to the hypotenuse, two similar right triangles are formed. This is known as the right triangle altitude theorem.

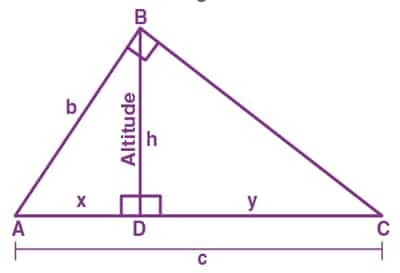
1706452282543

In the above triangle,

$△ADB ∼ △BDC$

Therefore

$\frac{AD}{BD}=\frac{BD}{DC}$

$BD^{2}=AD*DC$

$h^{2}=x*y$

$h=\sqrt{xy}$

Hence, this shows the altitude of a right triangle.

The formulas for the altitude are summed up in the following table.

Scalene Triangle	$h=\frac{2\sqrt{s. \left ( s-a \right ) .\left ( s-b \right ).\left ( s-c \right )}}{b}$
Isosceles Triangle	$h=\sqrt{\:a^{2}-\frac{b^{2}}{4}}$
Equilateral Triangle	$h=\frac{\sqrt{3}}{2}a$
Right Triangle	$h=\sqrt{xy}$

Difference Between Median and Altitude of Triangle

The median and the altitude of a triangle are the types of triangles whose line segments join the vertex to the opposite side of a triangle. They differ from each other

Let’s understand the difference table which is given below

Median of a Triangle	The altitude of a Triangle
The median of a triangle is the line segment which is drawn from the vertex to the opposite side of the triangle.	The altitude of a triangle is the perpendicular distance from the base to the opposite vertex of the triangle.
It always lies inside the triangle.	The altitude of a triangle can be both outside or inside of the triangle which depends upon the type of triangle.
Median of the triangle divides a triangle into two equal parts.	On the other hand, the altitude of a triangle may or may not divide any triangle into two equal parts.
The median of the triangle always bisects the base of the triangle in two equal parts.	The altitude of the triangle may or may not bisect the base of the triangle.
The centroid of the triangle is known as the point where all three medians of a triangle meet at a point.	The orthocenter of that triangle is defined as the point where all the three altitudes of the triangle meet each other.

Frequently Asked Questions (FAQs)

1. Define the altitude of the triangle?

The altitude of a triangle is defined as the perpendicular drawn from a vertex to the opposite side of the triangle.

2. Write the formula of the altitude of the triangle?

We can calculate the height or an altitude of a triangle by the formula which is given below-

Altitude=\frac{\lgroup 2*Area\rgroup}{Base}

3. What is an equilateral triangle?

A triangle in which all three sides are equal is said to be an equilateral triangle.

4. Write the formulas for the altitude of the Scalene Triangle.

The formulas for the altitude of the Scalene Triangle is

h=2\sqrt{s. \left ( s-a \right ) .\left ( s-b \right ).\left ( s-c \right )}/\:b

5. Can an altitude be outside the triangle?

Yes, in an obtuse triangle, two of the altitudes will fall outside the triangle. This happens because the perpendicular line from a vertex to the opposite side's extension falls outside the triangle's boundaries.

6. How does the concept of altitude apply to obtuse triangles?

In obtuse triangles, two of the altitudes fall outside the triangle. The altitude from the obtuse angle vertex is inside the triangle, while the other two extend to the opposite side's extension beyond the triangle's boundaries.

7. What is the orthocenter of a triangle?

The orthocenter is the point where all three altitudes of a triangle intersect. In acute triangles, it's inside the triangle; in right triangles, it's at the right angle vertex; and in obtuse triangles, it's outside the triangle.

8. How does the position of the orthocenter change with triangle type?

The position of the orthocenter varies:

9. What is the pedal triangle, and how does it relate to altitudes?

The pedal triangle is formed by connecting the feet of the three altitudes of a triangle. It has interesting properties, including that its orthocenter coincides with the original triangle's orthocenter, demonstrating a deep connection between altitudes and triangle geometry.

10. How do altitudes relate to the medians of a triangle?

While altitudes and medians are different (medians connect a vertex to the midpoint of the opposite side), they both intersect at a single point. The centroid (intersection of medians) and orthocenter (intersection of altitudes) are two of the four notable points in a triangle's geometry.

11. What is the difference between an altitude and a height of a triangle?

In a triangle, the terms "altitude" and "height" are often used interchangeably. Both refer to the perpendicular line segment from a vertex to the opposite side. However, "height" is sometimes used specifically when the triangle is in a standard position with a horizontal base.

12. How do you construct an altitude of a triangle using a compass and straightedge?

To construct an altitude:

13. What is the relationship between a triangle's area and the product of its semi-perimeter and radius of the inscribed circle?

The area of a triangle is equal to the product of its semi-perimeter and the radius of its inscribed circle. This relationship involves the altitudes, as the radius of the inscribed circle is related to the altitudes of the triangle.

14. Can you explain the concept of an Euler line using altitudes?

The Euler line is a straight line that passes through several important points in a triangle, including the orthocenter (intersection of altitudes). It demonstrates a fascinating relationship between various triangle centers, including those defined by the altitudes.

15. How do you find the equation of an altitude in a triangle given the coordinates of its vertices?

To find the equation of an altitude:

16. How many altitudes does a triangle have?

Every triangle has three altitudes, one from each vertex to the opposite side (or its extension). These altitudes intersect at a single point called the orthocenter.

17. What is the altitude of a triangle?

The altitude of a triangle is a line segment from a vertex perpendicular to the opposite side (or its extension). It's important to note that every triangle has three altitudes, one from each vertex.

18. How do you prove that the three altitudes of a triangle intersect at a single point?

To prove that the three altitudes intersect at a single point:

19. How does the length of an altitude change as you move its top point along the side of the triangle?

As you move the top point of an altitude along the side of a triangle, its length changes. It reaches its minimum when it becomes perpendicular to the opposite side. This illustrates why the true altitude must be perpendicular to achieve the shortest distance.

20. What is the relationship between the altitudes and the angle bisectors of a triangle?

While altitudes and angle bisectors are different lines, they both intersect at a single point within the triangle (except in obtuse triangles where the orthocenter is outside). The relationship between these lines helps define the geometry of the triangle.

21. How does the altitude relate to the area of a triangle?

The altitude is directly related to the area of a triangle through the formula: Area = (1/2) × base × height. Here, the altitude serves as the height, allowing us to calculate the area when we know the length of the base and the altitude.

22. What is the relationship between the altitudes and the area of a triangle?

The area of a triangle can be calculated using any of its three altitudes: Area = (1/2) × base × corresponding altitude. This means that the product of any side and its corresponding altitude is always twice the area of the triangle.

23. Why is the altitude important in calculating a triangle's area?

The altitude is crucial for calculating a triangle's area because it forms the height in the area formula: Area = (1/2) × base × height. The altitude provides the perpendicular height needed for this calculation.

24. How do you find the length of an altitude if you know the area and base of a triangle?

If you know the area (A) and base (b) of a triangle, you can find the length of the corresponding altitude (h) using the formula: h = (2 × A) ÷ b. This is derived from rearranging the area formula: A = (1/2) × b × h.

25. What is the significance of the foot of an altitude in a triangle?

The foot of an altitude is the point where the altitude intersects the opposite side (or its extension). It's significant because it creates a right angle with the side, which is crucial for area calculations and in defining the shortest distance from a point to a line.

26. What happens to the altitudes in a right triangle?

In a right triangle, one of the altitudes coincides with a leg of the triangle (the one perpendicular to the hypotenuse). The other two altitudes fall inside the triangle, and all three intersect at the vertex of the right angle.

27. What is the relationship between the altitudes and the sides of a right triangle?

In a right triangle, the altitude to the hypotenuse divides the triangle into two similar right triangles. This relationship is the basis for several important theorems, including the geometric mean theorem and the Pythagorean theorem.

28. What is the altitude-on-hypotenuse theorem?

The altitude-on-hypotenuse theorem states that in a right triangle, the altitude to the hypotenuse divides the triangle into two triangles that are similar to the original triangle and to each other. This theorem is crucial in proving other important relationships in right triangles.

29. How does the concept of altitude apply in trigonometry?

In trigonometry, altitudes are often used to define trigonometric ratios. For example, in a right triangle, the sine of an angle is the ratio of the opposite side (which is an altitude to the hypotenuse) to the hypotenuse.

30. How does the concept of altitude relate to the idea of distance in geometry?

The altitude represents the shortest distance from a point (vertex) to a line (opposite side). This concept is fundamental in geometry and extends to higher dimensions, forming the basis for understanding perpendicularity and distance in various geometric contexts.

31. In which type of triangle are all altitudes equal?

In an equilateral triangle, all three altitudes are equal. This is because an equilateral triangle has three equal sides and three equal angles, resulting in three congruent altitudes.

32. What is the relationship between the altitudes and the sides of an equilateral triangle?

In an equilateral triangle, each altitude is also an angle bisector and a median. The length of each altitude is √3/2 times the length of a side. This relationship showcases the special properties of equilateral triangles.

33. How does the study of altitudes in triangles contribute to understanding more complex geometric shapes?

The study of altitudes in triangles forms a foundation for understanding more complex shapes. Concepts like perpendicularity, distance, and area calculation using altitudes extend to polygons, 3D shapes, and even abstract geometric spaces, making triangle altitudes a fundamental concept in advanced geometry.

34. What is the significance of the orthocenter in the study of triangle centers?

The orthocenter, as the intersection of altitudes, is one of the four major triangle centers (along with the centroid, circumcenter, and incenter). Its position relative to the triangle and its relationships with other centers provide insights into the triangle's shape and properties.

35. Can two altitudes of a triangle be equal?

Yes, two altitudes of a triangle can be equal. This occurs in isosceles triangles, where the altitudes to the two equal sides are congruent.

36. How do you use altitudes to solve optimization problems in triangles?

Altitudes are often used in optimization problems, such as finding the shortest distance from a point to a line or determining the triangle with the largest area given certain constraints. These problems often involve calculus and demonstrate practical applications of triangle geometry.

37. How does the concept of altitude apply in trigonometric proofs?

Altitudes are often used in trigonometric proofs, especially those involving right triangles. They help establish relationships between sides and angles, and are crucial in deriving trigonometric identities and solving complex trigonometric problems.

38. What is the role of altitudes in determining the type of a triangle (acute, right, or obtuse)?

The position of the orthocenter (intersection of altitudes) determines the triangle type:

39. What is the role of altitudes in understanding similarity of triangles?

Altitudes play a crucial role in proving similarity of triangles, especially in right triangles. The altitude to the hypotenuse creates two triangles similar to the original, which is fundamental in many geometric proofs and applications.

40. How do you calculate the length of an altitude using trigonometry?

To calculate the length of an altitude using trigonometry:

41. How do you find the coordinates of the orthocenter in a triangle given the coordinates of its vertices?

To find the orthocenter's coordinates:

42. How do you prove that the product of two sides of a triangle is equal to the product of the diameter of the circumcircle and the altitude to the third side?

This proof involves:

43. What is the relationship between the altitudes and the area of the orthic triangle?

The orthic triangle is formed by connecting the feet of the altitudes. Its area is related to the original triangle's area and involves the lengths of the altitudes. This relationship provides another way to explore the geometry of triangles through their altitudes.

44. What is the role of altitudes in proving the Pythagorean theorem?

One proof of the Pythagorean theorem involves drawing an altitude from the right angle to the hypotenuse. This creates similar triangles, which can be used to establish relationships between the sides and ultimately prove a² + b² = c².

45. How does the concept of altitude apply to non-Euclidean geometries?

In non-Euclidean geometries, such as spherical or hyperbolic geometry, the concept of altitude still exists but may behave differently. For example, on a sphere, the "altitude" might be an arc of a great circle perpendicular to another great circle.

46. How does the concept of altitude extend to three-dimensional geometry?

In three-dimensional geometry, the concept of altitude extends to the height of a solid. For example, in a pyramid or cone, the altitude is the perpendicular line segment from the apex to the base plane. This is crucial for volume calculations of 3D shapes.

47. How does the concept of altitude extend to higher dimensions in geometry?

In higher dimensions, the concept of altitude generalizes to the idea of orthogonal projection. For example, in a tetrahedron, an altitude is a line segment from a vertex perpendicular to the opposite face. This extends the 2D concept to 3D and beyond.

48. What is the relationship between the altitudes and the circumcenter of a triangle?

The circumcenter (the intersection of the perpendicular bisectors of the sides) and the orthocenter (intersection of altitudes) are always collinear with the centroid. This relationship is part of the Euler line concept in triangle geometry.

49. What is the relationship between the altitudes and the incenter of a triangle?

While the altitudes intersect at the orthocenter, the angle bisectors intersect at the incenter. These points, along with the centroid and circumcenter, form part of the study of triangle centers, each with unique properties related to the triangle's geometry.

50. What is the role of altitudes in the nine-point circle theorem?

The nine-point circle theorem states that the feet of the three altitudes of a triangle, along with six other significant points, all lie on a single circle. This demonstrates the deep connection between altitudes and other elements of triangle geometry.

51. How does the concept of altitude apply to obtuse-angled triangles?

In obtuse-angled triangles, two of the altitudes fall outside the triangle. This doesn't change their definition or importance but affects their visualization and can make certain calculations more complex.

52. What is the significance of the Euler's theorem relating the orthocenter, centroid, and circumcenter?

Euler's theorem states that the orthocenter (H), centroid (G), and circumcenter (O) of a triangle are collinear, and that OG:GH = 1:2. This theorem, which involves the altitudes (through the orthocenter), reveals a fundamental relationship in triangle geometry.

53. How do you prove that the centroid divides each median in the ratio 2:1, and how does this relate to altitudes?

While this proof primarily involves medians, understanding it helps in grasping the relationship between various triangle centers, including the orthocenter (intersection of altitudes). The proof typically uses similar triangles and area relationships.

54. What is the relationship between the altitudes and the area of the medial triangle?

The medial triangle is formed by connecting the midpoints of the sides of the original triangle. Its area is 1/4 of the original triangle's area. While this doesn't directly involve altitudes, understanding this relationship helps in comprehending how different triangle elements relate to area.