Area of Parallelogram (Definition, Formulas & Examples)
A parallelogram is a figure which is found commonly around us in the form of parks, fields, buildings, etc. The area of parallelogram is a region covered by a parallelogram in an x-y plane. It is the space within its four sides. Hence it is equal to the product of length and height of the parallelogram. From our prior knowledge, we know that the sum of interior angles of a quadrilateral is 360 degrees. Since it is a 2-D figure, we have the concept of perimeter and area of parallelogram. The area is always measured in sq units like sq m, sq cm, etc. This concept of area of parallelogram has wide range of applications in daily life such as architecture, engineering, windows, tables, laptops, and much more.
This Story also Contains
- What is the Area of Parallelogram?
- How to find Area of Parallelogram?
- Area of Parallelogram Vectors
- Perimeter and Area of Parallelogram
- Solved Examples based on Area of Parallelogram
This article is about the concepts of area of parallelogram, formula of area of parallelogram, area of parallelogram vectors, area of parallelogram with diagonals, perimeter and area of parallelogram, etc.

What is the Area of Parallelogram?
The area of a parallelogram is the region or space covered by the parallelogram in a given 2-D plane or x-y space. If we talk about the properties of a parallelogram, we can say that it is a special type of quadrilateral having the pair of opposite sides as parallel, the opposite sides being of equal length and opposite angles being of equal measures. These few properties make it different from a square or a rectangle which are also classified as quadrilaterals in geometry.
Area of Parallelogram Formula

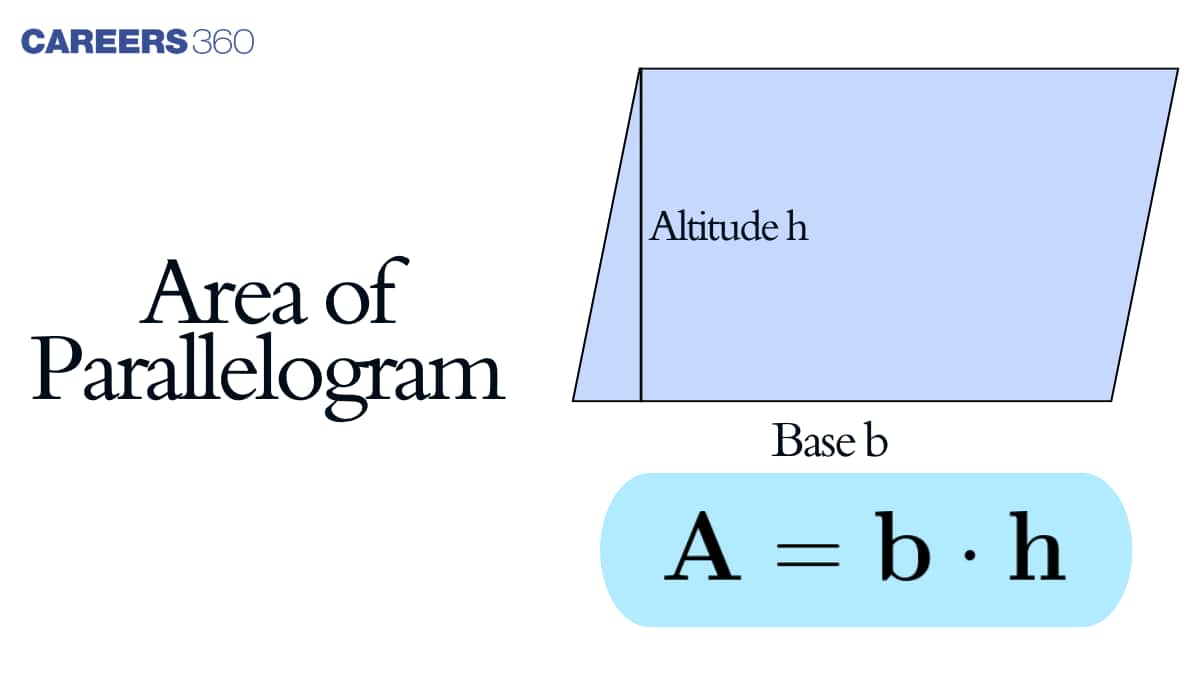
If we wish to find the area of parallelogram, we have to multiply the base of the perpendicular of parallelogram by its height. We must remember certain points that the base and the height of the parallelogram are always perpendicular to each other, which means they form an angle of 90 degrees wherever they meet or intersect, whereas the lateral side of the parallelogram is not perpendicular to the base, hence angle measuring 90 degrees is not formed at their meeting point. The formula for area of parallelogram is given as:
Area $=b \times h$ Square units
Where "b" = base and " $h$ " = height
How to find Area of Parallelogram?
Area of parallelogram can be calculated using its base and height. Apart from that, the area of parallelogram can also be calculated if its two diagonals are known along with any of their intersecting angles or if the length of the parallel sides is known, along with any of the angles between the sides. Following are the ways to find the area of parallelogram depending upon which sides are unknown to us and which are known:
- When the base and height of the parallelogram are given
- When height is not given
- When diagonals are given
Area of Parallelogram Using Sides
Suppose a and b are the set of parallel sides of a parallelogram and h is the height, then based on the length of sides and height of it, the formula for area of parallelogram is given by:
area of parallelogram = Base × Height
$\mathrm{A}=\mathrm{b} \times \mathrm{h} \quad$ [sq.unit]
Example: What is the area of parallelogram if the base of parallelogram is equal to 10 cm and the height is 5 cm ?
Solution: Given, the length of base $=10 \mathrm{~cm}$ and height $=5 \mathrm{~cm}$
As per the formula of area of parallelogram, area $=10 \times 5= 50$ sq.cm
Area of Parallelogram Without Height
If the height of the parallelogram is unknown to us, then we can use the trigonometry concept here to find area of parallelogram. However, this particular case is rarely used but we can remember it for few cases.
Formula for area of parallelogram $=\mathrm{ab} \sin (\mathrm{x})$
Where $a$ and $b$ are the length of adjacent sides of the parallelogram and $x$ is the angle between the sides of the parallelogram.
Area of Parallelogram with Diagonals
The area of parallelogram can also be calculated using its diagonal lengths. Since we know, there are two diagonals for a parallelogram, which intersect each other. Suppose the diagonals intersect each other at an angle $y$, then the area of parallelogram is given by:
area of parallelogram formula $=\frac{1}{2} \times d_1 \times d_2 \sin (y)$
Following table summarises various formula for area of parallelogram :
| Using Base and Height | $A = b × h$ |
| Using Trigonometry | $A = ab \sin (x)$ |
| Using Diagonals | $A = \frac{1}{2} \times d_1 \times d_2 \sin (y)$ |
Where,
- $b=$ base of the parallelogram (AB)
- $h=$ height of the parallelogram
- $\mathrm{a}=$ side of the parallelogram (AD)
- $x=$ any angle between the sides of the parallelogram ( $\angle \mathrm{DAB}$ or $\angle \mathrm{ADC}$ )
- $\mathrm{d}_1=$ diagonal of the parallelogram $(p)$
- $\mathrm{d}_2=$ diagonal of the parallelogram $(q)$
- $y=$ any angle at the intersection point of the diagonals ( $\angle \mathrm{DOA}$ or $\angle \mathrm{DOC})$
Area of Parallelogram Vectors
If the sides of a parallelogram are given in vector form, then the area of parallelogram can be calculated using its sides, if the sides are not given then the area of parallelogram can be calculated using its diagonals.
Let vector ‘$a$’ and vector ‘$b$’ be the two sides of a parallelogram.
Area of parallelogram in vector form using the sides of the parallelogram= Mod of cross-product of vector $a$ and vector $ b$
Hence, area of parallelogram $=$ Mod of cross-product of vector $a$ and vector $b$
$
A=|a \times b|
$
Now, we can find the area of parallelogram with respect to diagonals, say $d_1$ and $d_2$, in vector form.
Suppose vector ‘$a$’ and vector ‘$b$’ are the two sides of a parallelogram, such that the resulting vector is the diagonal of the parallelogram.
So, we can write;
$
\begin{aligned}
& a+b=d_1 \\
& b+(-a)=d_2
\end{aligned}
$
or
$
b-a=d_2
$
Thus,
$
\begin{aligned}
& d_1 \times d_2=(a+b) \times(b-a) \\
& =a \times(b-a)+b \times(b-a) \\
& =a \times b-a \times a+b \times b-a \times b \\
& =a \times b-0+0-b \times a \\
& =a \times b-b \times a
\end{aligned}
$
$
a \times b=-b \times a
$
Therefore,
$
\begin{aligned}
& d_1 \times d_2=a \times b+a \times b=2(a \times b) \\
& a \times b=\frac{1}{2} \left(d_1 \times d_2\right)
\end{aligned}
$
Hence,
Area of parallelogram, when diagonals are given in the vector form becomes:
$
A=\frac{1}{2} \left(d_1 \times d_2\right)
$
Perimeter and Area of Parallelogram
We know that the area of parallelogram is equal to the product of base and height.
$\mathrm{A}=\mathrm{b} \times \mathrm{h}$ square units
The relationship between perimeter and area of parallelogram is:
$P=2(a+b)$ units
Therefore, the value of $b$ in terms of $P$ is
$
\begin{aligned}
& \frac{P}{2}=\mathrm{a}+\mathrm{b} \\
& \mathrm{~b}=(\frac{P}{2})-\mathrm{a}
\end{aligned}
$
Now, substitute the value of $b$ in (1)
$A=((\frac{P}{2})-a) h$ Square units
Solved Examples based on Area of Parallelogram
Example 1: What is the area of parallelogram with a base of 2 cm and height of 5 cm .
Solution:
Given:
Base, $b=2 \mathrm{~cm}$
$
\mathrm{h}=5 \mathrm{~cm}
$
We know that,
Formua for Area of Parallelogram $=\mathrm{b} \times \mathrm{h}$ Square units
$
=2 \times 5=10 \mathrm{sq} . \mathrm{cm}
$
Therefore, the area of parallelogram $=20 \mathrm{~cm}^2$
Example 2: Find the area of parallelogram whose breadth is 4 cm and height is 10 cm .
Solution:
Given,
$
\begin{aligned}
& \mathrm{b}=4 \mathrm{~cm} \\
& \mathrm{~h}=10 \mathrm{~cm}
\end{aligned}
$
The area of parallelogram is
$
\begin{aligned}
& =\mathrm{b} \times \mathrm{h} \\
& =4 \times 10 \mathrm{~cm}^2 \\
& =40 \mathrm{~cm}^2
\end{aligned}
$
Example 3: The base of the parallelogram is thrice its height. If the area of parallelogram is $190 \mathrm{~cm}^2$, find the base and height.
Solution:
Let the height of the parallelogram $=\mathrm{h} \mathrm{cm}$
then, the base of the parallelogram $=3 \mathrm{~h} \mathrm{~cm}$
Area of parallelogram $=190 \mathrm{~cm}^2$
Hence, formula for area of parallelogram $=$ base $\times$ height
Therefore, $190=3 \mathrm{~h} \times \mathrm{h}$
$
\begin{aligned}
& \Rightarrow 3 \times \mathrm{h}^2=190 \\
& \Rightarrow \mathrm{~h}^2=63.33=63 \text { (approx) } \\
& \Rightarrow \mathrm{h}=7.9 \mathrm{~cm}
\end{aligned}
$
Hence, the height of the parallelogram is 8 cm , and breadth is
$
\begin{aligned}
& 3 \times \mathrm{h} \\
& =3 \times 7.9 \\
& =23.7 \mathrm{~cm} \mathrm{sq}
\end{aligned}
$
Example 4: The area of a parallelogram is $500 \mathrm{sq.cm}$. Its height is twice its base. Find the height and base.
Solution:
Given, area $=500$ sq.cm.
Height $=$ Twice of base
$
h=2 b
$
By the formula, we know,
Area of parallelogram is $=\mathrm{b} \times \mathrm{h}$
$
\begin{aligned}
& 500=b \times 2 b \\
& 2 b^2=500 \\
& b^2=250 \\
& b=15.8 \mathrm{~cm}
\end{aligned}
$
Hence, height $=2 \times b=31.6 \mathrm{~cm}$
Example 5: Calculate the area of a solar sheet that is in the shape of a parallelogram, given that, the base measures 10 in , and the altitude measures 8 in.
Solution:
Area of parallelogram $=$ Area of the solar sheet $=\mathrm{B} \times \mathrm{H}=(10) \times(8)=80 \mathrm{in}^2$
For more such examples refer Area of parallelogram worksheet.
List of Topics Related to Area of Parallelogram
| Area of Circle | Area of Isosceles Triangle |
| Area of Rectangle | Area of Sphere |
| Area | Area of Quadrilateral |
| Area of Square | Area and Perimeter |
| Area of Equilateral Triangle | cm to inches converter |
Frequently Asked Questions (FAQs)
The area of parallelogram can be calculated when the adjacent sides or diagonals are given in vector form. Formula of area of parallelogram is given by: $|\mathbf{a} \times \mathbf{b}|$, where $\mathbf{a}$ and $\mathbf{b}$ are adjacent side vectors. Also, the area of parallelogram formula using diagonals in vector form is, area of parallelogram $= \frac{1}{2} \left|\left(\mathbf{d}_{\mathbf{1}} \times \mathbf{d}_{\mathbf{2}}\right)\right|$, where $\mathbf{d}_{\mathbf{1}}$ and $\mathbf{d}_{\mathbf{2}}$ are diagonal vectors.
The area of parallelogram is expressed as :
Area of $=$ base $\times$ height.
If we wish to find the perimeter of parallelogram, we add all the sides together. The following formula gives the perimeter of any parallelogram:
Perimeter of parallelogram $=2(a+b)$
The area of a perpendicular with height 2 cm and base 4 cm will be:
Area of parallelogram is $=\mathrm{b} \times \mathrm{h}$
Or, Area of parallelogram $=2 \times 5=10 \mathrm{~cm}^2$
