Area of Quadrilateral - Introduction, Formulae, Calculations
The area of a quadrilateral is a fundamental concept in geometry that measures the total space enclosed within its four sides. Whether the shape is a square, rectangle, trapezium, or any irregular four-sided figure, understanding the area of a quadrilateral formula helps in solving both academic problems and real-life applications. The formula of a quadrilateral can vary depending on its type and available measurements, making it essential to know the right approach for each case. If you are wondering what is the area of a quadrilateral and how to calculate it accurately, this article will give you clear explanations and practical examples in mathematics. In this article, we will explore the different formulas and methods for finding the area of quadrilaterals in detail.
This Story also Contains
- What is the Area of a Quadrilateral?
- Area of a Quadrilateral Formula
- Area of a Quadrilateral Formula Using Different Conditions
- Different Types of Quadrilaterals and Their Area Formulas
- Area of a Quadrilateral Formula in Coordinate Geometry
- Area of a Quadrilateral in Vector Form
- Solved Examples based on Area of Quadrilaterals
- List of Topics Related to the Area of a Quadrilateral
- NCERT Resources
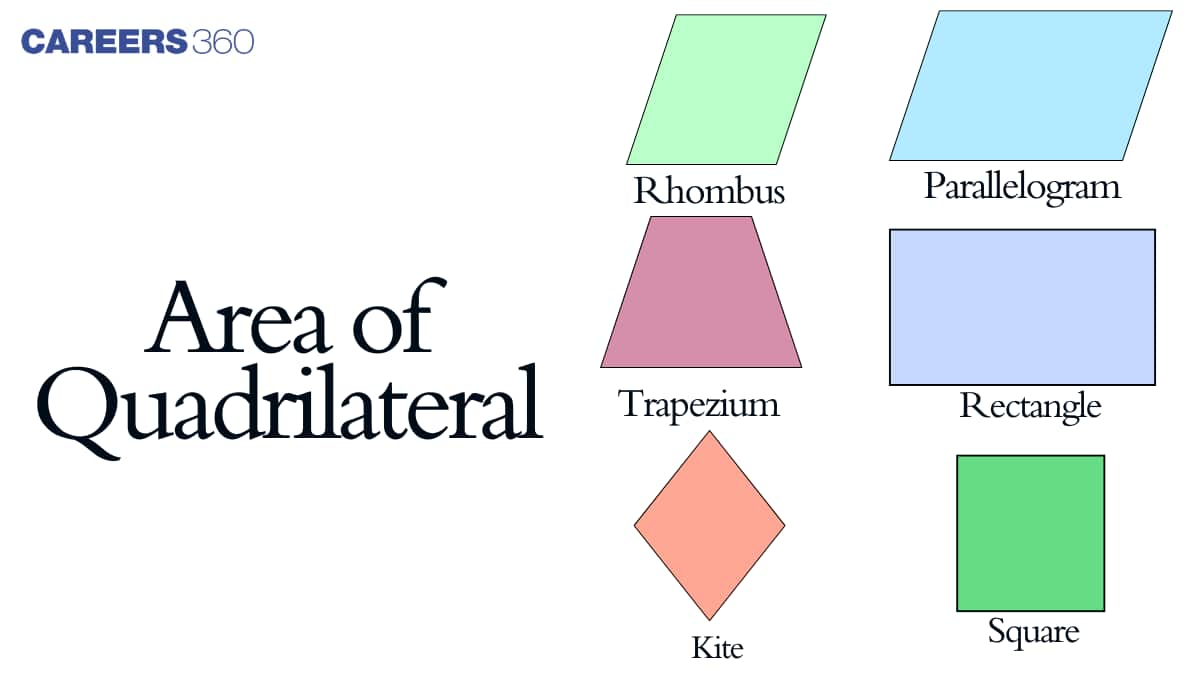
What is the Area of a Quadrilateral?
The area of a quadrilateral refers to the total two-dimensional space enclosed within its four sides. A quadrilateral is a closed polygon with four straight sides and four vertices, and its area is expressed in square units such as $cm^2$, $m^2$, or $km^2$. The area of a quadrilateral formula is not fixed for all cases; it depends on the type of quadrilateral and the information provided, such as side lengths, diagonals, or angles. Whether the shape is regular, like a square or irregular, like an arbitrary four-sided plot, understanding what is the area of a quadrilateral is essential for accurate calculations.
Definition of a Quadrilateral in Geometry
In geometry, a quadrilateral is defined as a polygon with four sides $(AB, BC, CD, DA)$, four vertices $(A, B, C, D)$, and four angles whose sum is always $360^\circ$. Quadrilaterals can be classified into various types, including parallelograms, rectangles, squares, trapeziums, rhombuses, kites, and irregular forms. The formula of quadrilateral for finding its area varies based on these classifications. For example:
If all sides are equal and angles are right angles (square), the area is calculated as $Area = a^2$.
If opposite sides are equal and parallel (rectangle), the formula is $Area = l \times b$.
Understanding the Concept of Area in a Quadrilateral
The area of a quadrilateral measures the extent of the surface it covers. In mathematical terms, for certain quadrilaterals, the area can be found using basic formulas such as $Area = base \times height$, while for others, more complex formulas like $Area = \frac{1}{2} \times d_1 \times d_2 \times \sin\theta$ (where $d_1$ and $d_2$ are diagonals, and $\theta$ is the angle between them) are used. Understanding which area of the quadrilateral formula applies is crucial for solving both theoretical and practical problems.
Real-Life Applications of the Area of a Quadrilateral
The concept of the area of a quadrilateral has several real-world applications. It is used in calculating the land area of rectangular or trapezium-shaped plots, designing floor plans, estimating materials needed for square or rhombus-shaped tiles, or even determining the coverage area of kites and banners. For example, if a farmer’s plot is in the shape of an irregular quadrilateral, breaking it into triangles and applying Heron’s formula helps in determining its total area. Knowing the area of a quadrilateral and how to apply the right formula ensures precision in such tasks.
Area of a Quadrilateral Formula
The formula of the area of a quadrilateral can be determined using different methods, such as dividing the quadrilateral into two triangles, applying Heron’s formula, or using the lengths of its sides along with angles or diagonals. Depending on the values provided in the question, we can choose the most suitable formula to make our calculations simpler and more efficient. Let us now look at each method one by one.
How to find the Area of a Quadrilateral by Dividing Into Two Triangles?
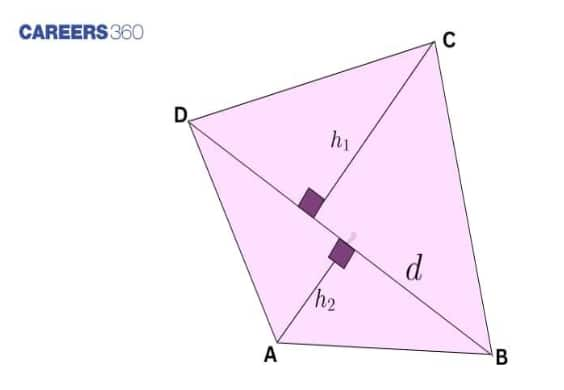
Consider a quadrilateral $ABCD$ in which the length of the diagonal $BD$ is known to be $d$. The diagonal $BD$ divides the quadrilateral into two triangles: $\triangle ABD$ and $\triangle BCD$. To find the total area, we must know the heights of these triangles. Let the heights of $\triangle ABD$ and $\triangle BCD$ (perpendicular to $BD$) be $h_1$ and $h_2$ respectively.
The area of $\triangle ABD$ is:
$Area_{ABD} = \frac{1}{2} \times d \times h_1$
The area of $\triangle BCD$ is:
$Area_{BCD} = \frac{1}{2} \times d \times h_2$
Therefore, the total area of quadrilateral $ABCD$ is:
$Area_{ABCD} = Area_{ABD} + Area_{BCD}$
$Area_{ABCD} = \frac{1}{2} \times d \times h_1 + \frac{1}{2} \times d \times h_2$
$Area_{ABCD} = \frac{1}{2} \times d \times (h_1 + h_2)$
Thus, the formula used to find the area of a quadrilateral when one of its diagonals and the heights of the triangles formed by it are known is:
$Area = \frac{1}{2} \times \text{Diagonal} \times (\text{Sum of heights})$
Area of a Quadrilateral Formula Using Different Conditions
The area of a quadrilateral formula can be applied in different ways depending on the given information. Two common cases include:
Area of a quadrilateral formula with sides given
Area of a quadrilateral using Heron’s formula
Area of a Quadrilateral Formula with Sides Given
When the lengths of all four sides and the measures of two opposite angles are known, we can calculate the area using Bretschneider’s formula.
Let the quadrilateral have sides $e$, $f$, $g$, and $h$, and two opposite angles $\theta_1$ and $\theta_2$ as shown in the figure. The formula is:
$Area = \sqrt{(s-e)(s-f)(s-g)(s-h) - e f g h \cos^2 \frac{\theta}{2}}$
where:
$s = \frac{(e+f+g+h)}{2}$ is the semi-perimeter of the quadrilateral
$\theta = \theta_1 + \theta_2$ is the sum of the given opposite angles
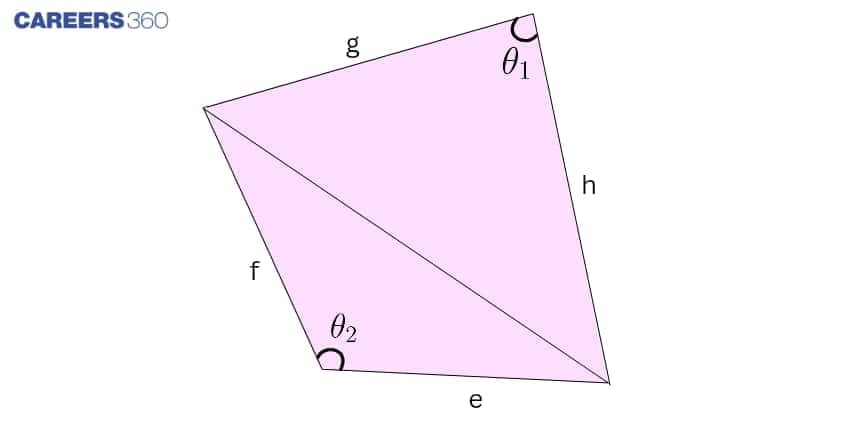
This formula works for both cyclic and non-cyclic quadrilaterals, making it a versatile formula of quadrilaterals when side lengths and angles are known.
Area of a Quadrilateral Using Heron’s Formula
We already know that the area of a triangle with sides $x$, $y$, and $z$ is given by:
$Area_{\triangle} = \sqrt{s(s-x)(s-y)(s-z)}$
where $s = \frac{(x+y+z)}{2}$ is the semi-perimeter of the triangle.
To find the area of a quadrilateral using Heron’s formula, follow these steps:
Divide the quadrilateral into two triangles using a diagonal whose length is known.
Apply Heron’s formula to each triangle individually to find its area.
Add the areas of the two triangles to get the total area of the quadrilateral.
This method is especially useful for irregular quadrilaterals when no direct area of a quadrilateral formula applies, but all side lengths and one diagonal are known.
Different Types of Quadrilaterals and Their Area Formulas
Quadrilaterals come in various shapes, and the area of a quadrilateral formula changes depending on the type and available measurements. While some formulas are straightforward, others require diagonals, angles, or even trigonometric functions. Understanding the specific formula of a quadrilateral for each type ensures accurate results in both academic and practical applications.
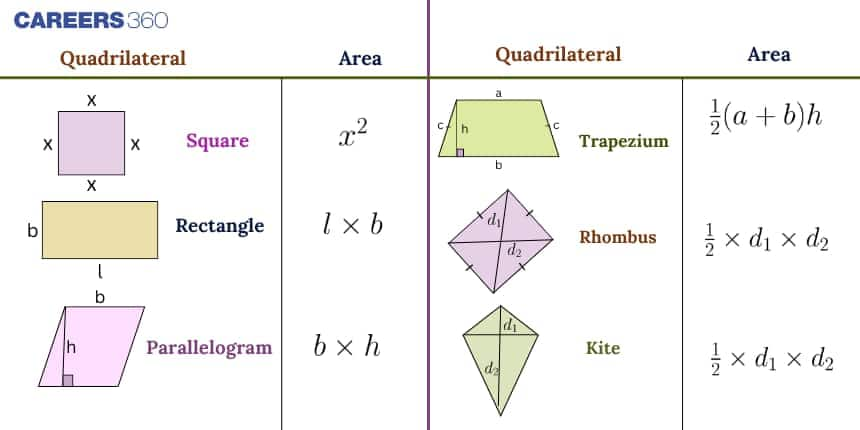
Area of a Square Formula
A square is a regular quadrilateral with all sides equal and all angles measuring $90^\circ$. The area of a quadrilateral formula for a square is:
$Area = a^2$
where $a$ is the length of any side.
Example: If $a = 5 , cm$, then $Area = 5^2 = 25 , cm^2$.
Area of a Rectangle Formula
A rectangle has opposite sides equal and parallel, with each angle measuring $90^\circ$. The formula of a quadrilateral in this case is:
$Area = l \times b$
where $l$ is length and $b$ is breadth.
Example: If $l = 8 , m$ and $b = 5 , m$, then $Area = 8 \times 5 = 40 , m^2$.
Area of a Parallelogram Formula
A parallelogram has opposite sides equal and parallel, but does not necessarily have right angles. The area of a quadrilateral formula is:
$Area = base \times height$
Or $Area = a \times b \times \sin\theta$
where $a$ and $b$ are adjacent sides, and $\theta$ is the included angle.
Area of a Trapezium Formula
A trapezium (or trapezoid) has one pair of parallel sides. Its area of a quadrilateral formula is:
$Area = \frac{1}{2} \times (a + b) \times h$
where $a$ and $b$ are the lengths of the parallel sides, and $h$ is the height.
Area of a Rhombus Formula
A rhombus is a quadrilateral with all sides equal and opposite angles equal. The most common formula of a quadrilateral for a rhombus is:
$Area = \frac{1}{2} \times d_1 \times d_2$
where $d_1$ and $d_2$ are the lengths of the diagonals.
Area of a Kite Formula
A kite has two pairs of adjacent equal sides, and its area formula is similar to that of a rhombus:
$Area = \frac{1}{2} \times d_1 \times d_2$
where $d_1$ and $d_2$ are its diagonals.
Area of Irregular Quadrilateral Formula
An irregular quadrilateral does not have equal sides, equal angles, or parallel sides. The area of a quadrilateral in such cases is often calculated by dividing it into two triangles and applying Heron’s formula:
$Area = \sqrt{s(s-a)(s-b)(s-c)}$
for each triangle, where $s = \frac{a+b+c}{2}$. The total area is the sum of the two triangle areas.
Now, let us look into the area of quadrilateral in coordinate geometry.
Area of a Quadrilateral Formula in Coordinate Geometry
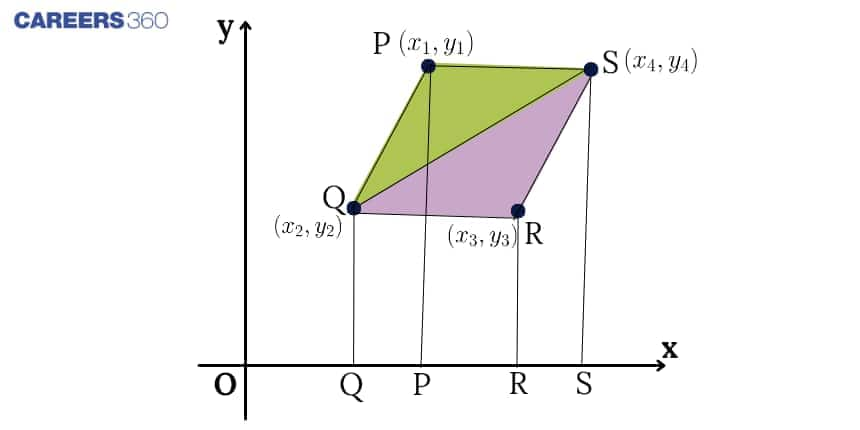
The area of a quadrilateral formula in coordinate geometry is useful when the vertices of the quadrilateral are given in the Cartesian plane.
Consider a quadrilateral $PQRS$ with vertices:
$P(x_1, y_1)$, $Q(x_2, y_2)$, $R(x_3, y_3)$, and $S(x_4, y_4)$.
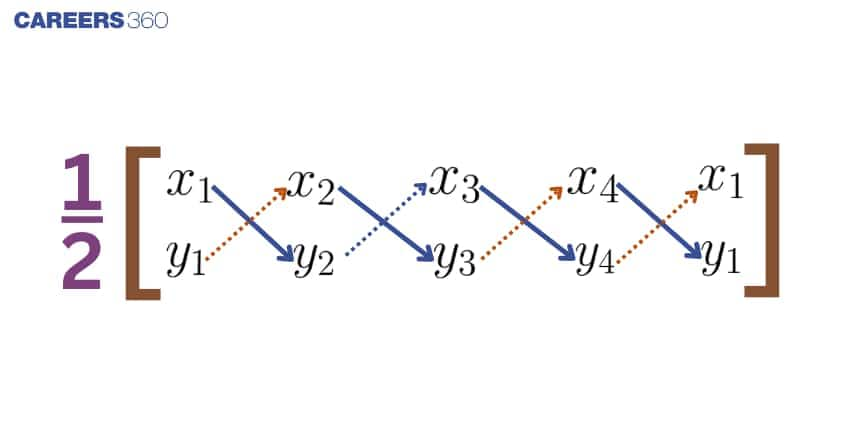
To find the area, follow these steps:
Arrange the coordinates cyclically in the order $P \to Q \to R \to S \to P$.
Add the products of coordinates along the forward (blue arrow) diagonals:
$Sum_1 = (x_1 y_2 + x_2 y_3 + x_3 y_4 + x_4 y_1)$
Add the products of coordinates along the backwards (orange arrow) diagonals:
$Sum_2 = (x_2 y_1 + x_3 y_2 + x_4 y_3 + x_1 y_4)$
Subtract $Sum_2$ from $Sum_1$, take the absolute value, and multiply by $\frac{1}{2}$:
$A = \frac{1}{2} \left| (x_1 y_2 + x_2 y_3 + x_3 y_4 + x_4 y_1) - (x_2 y_1 + x_3 y_2 + x_4 y_3 + x_1 y_4) \right|$
Area of a Quadrilateral in Vector Form
The area of a quadrilateral can also be expressed using vector operations. The method is based on dividing the quadrilateral into two triangles and then adding their vector areas.
Consider a quadrilateral $ABCD$. If it is divided into two triangles $\triangle ABC$ and $\triangle ACD$ using the diagonal $AC$, then:
Area of $\triangle ABC$ in vector form is:
$Area_{ABC} = \frac{1}{2} , \left| \overrightarrow{AB} \times \overrightarrow{AC} \right|$Area of $\triangle ACD$ in vector form is:
$Area_{ACD} = \frac{1}{2} , \left| \overrightarrow{AC} \times \overrightarrow{AD} \right|$
Therefore, the area of the quadrilateral in vector form is:
$Area_{ABCD} = \frac{1}{2} , \left| \overrightarrow{AB} \times \overrightarrow{AC} \right| + \frac{1}{2} , \left| \overrightarrow{AC} \times \overrightarrow{AD} \right|$
Solved Examples based on Area of Quadrilaterals
Example 1: Find the area of a rectangle whose length is 20 in and whose width is 15 in.
Solution:
The length of the rectangle is $l = 20$ in.
Its breadth is $b = 15$ in.
Using the formula of the area of a quadrilateral (rectangle), the area ($A$) of the given rectangle is: $A = l \times b$
$A = 20 \times 15$
$A = 300 \ \mathrm{in}^2$
Example 2: Find the area of a kite whose diagonals are 16 units and 12 units.
Solution:
The diagonals of the kite are $d_1 = 16$ units and $d_2 = 12$ units.
The area ($A$) of the given kite is:
$A = \frac{1}{2} \times d_1 \times d_2$
$A = \frac{1}{2} \times 16 \times 12$
$A = 96 \ \mathrm{units}^2$
Example 3: Calculate area of quadrilateral shown below.
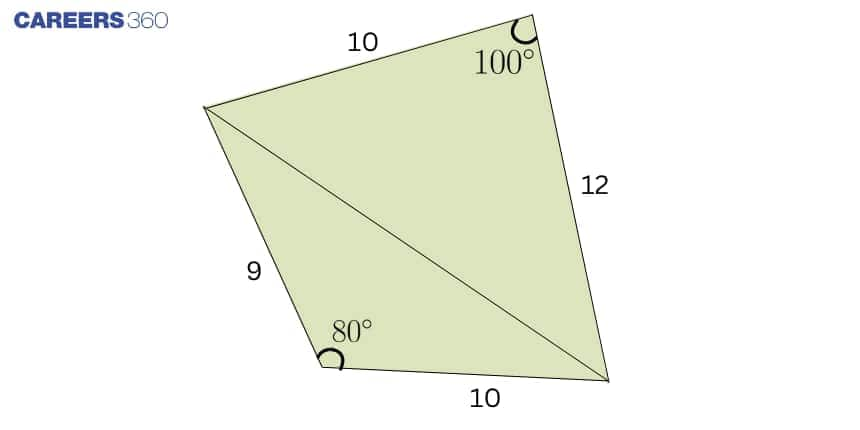
Solution: The sides are $p=10$, $q=12$, $r=9$, $s=10$.
Semi-perimeter: $s=\dfrac{(p+q+r+s)}{2}=\dfrac{10+12+9+10}{2}=20.5$.
Sum of opposite angles: $\theta=100^\circ+80^\circ=180^\circ$.
Using Bretschneider’s formula:
$A=\sqrt{(s-p)(s-q)(s-r)(s-s) - (p\cdot q\cdot r\cdot s)\cos^2\left(\dfrac{\theta}{2}\right)}$.
Compute the factors:
$(s-p)=20.5-10=10.5$
$(s-q)=20.5-12=8.5$
$(s-r)=20.5-9=11.5$
$(s-s)=20.5-10=10.5$
Product of these four factors:
$(s-p)(s-q)(s-r)(s-s)=10.5\times 8.5\times 11.5\times 10.5=10776.9375$.
The second term uses $\cos^2\left(\dfrac{\theta}{2}\right)=\cos^2(90^\circ)=0$, so
$(p\cdot q\cdot r\cdot s)\cos^2\left(\dfrac{\theta}{2}\right)=10800\times 0=0$.
Thus the area is:
$A=\sqrt{10776.9375 - 0}=\sqrt{10776.9375}=103.8120296497\ldots$
Rounded to three decimal places the area is:
$103.812\ \text{square units}$.
Example 4: Calculate the area of the quadrilateral formed by the vertices $(-4,2),\ (2,4),\ (8,-6)$ and $(-5,-4)$.
Solution:
Let $P(-4,2)=(x_1,y_1)$, $Q(2,4)=(x_2,y_2)$, $R(8,-6)=(x_3,y_3)$, $S(-5,-4)=(x_4,y_4)$.
Use the shoelace (coordinate) formula:
$A=\dfrac{1}{2}\left| (x_1y_2+x_2y_3+x_3y_4+x_4y_1) - (x_2y_1+x_3y_2+x_4y_3+x_1y_4) \right|$.
Compute the forward sum:
$x_1y_2 = -4\times 4 = -16$
$x_2y_3 = 2\times(-6) = -12$
$x_3y_4 = 8\times(-4) = -32$
$x_4y_1 = -5\times 2 = -10$
$Sum_1 = -16 -12 -32 -10 = -70$.
Compute the backward sum:
$x_2y_1 = 2\times 2 = 4$
$x_3y_2 = 8\times 4 = 32$
$x_4y_3 = -5\times(-6) = 30$
$x_1y_4 = -4\times(-4) = 16$
$Sum_2 = 4 + 32 + 30 + 16 = 82$.
Now the area is:
$A = \dfrac{1}{2}\left| -70 - 82 \right| = \dfrac{1}{2}\left| -152 \right| = \dfrac{152}{2} = 76$.
So the area is $76\ \text{square units}$.
Example 5: Find the area of a quadrilateral with a diagonal $=20$ and heights $h_1=7\ \text{cm},\ h_2=5\ \text{cm}$.
Solution:
When one diagonal and the corresponding heights to that diagonal are given, use
$Area = \dfrac{1}{2}\times (\text{Diagonal}) \times (h_1+h_2)$.
Substituting values:
$Area = \dfrac{1}{2} \times 20 \times (7+5)$
$Area = \dfrac{1}{2} \times 20 \times 12$
$Area = 10 \times 12 = 120$.
So the area is $120\ \text{cm}^2$.
List of Topics Related to the Area of a Quadrilateral
The concept of the area of a quadrilateral is closely linked to several other geometry and measurement topics. Exploring these related topics, such as the area of different shapes, unit conversions, and perimeter calculations, helps build a stronger foundation for solving diverse mathematical problems. Below is a list of topics that complement your understanding of quadrilateral area and its applications.
NCERT Resources
Mastering the area of quadrilaterals becomes easier with well-structured study materials. NCERT resources, including notes, solutions, and NCERT exemplar solutions for Class 9 Maths Chapter 8: Quadrilaterals, provide clear explanations, step-by-step problem solving, and practice exercises. These resources are designed to strengthen conceptual understanding and enhance problem-solving skills.
NCERT Notes for Class 9 Maths Chapter 8 - Quadrilaterals
NCERT Solutions for Class 9 Maths Chapter 8 - Quadrilaterals
NCERT Exemplar Solutions for Class 9 Maths Chapter 8 - Quadrilaterals
Frequently Asked Questions (FAQs)
The area of quadrilateral is the space occupied by the shape in xy plane.
They include Square, Rectangle, Rhombus, etc.
Formula for area of quadrilateral $=(\frac{1}{2}) \times$ Diagonal $\times$ (Sum of heights)
They are commonly used in the field of architecture, agriculture, designing, etc.
Formula of area of quadrilateral $=(\frac{1}{2}) \times$ Diagonal $\times($ Sum of heights $)= \frac{1}{2} \times 10 \times$ $8=40$ sq units.